Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ryady_metod_ukazaniya_kgasu_5354

.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

311.15 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра высшей математики

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Методические указания для самостоятельной работы студентов второго курса бакалавриата дневного отделения направлений подготовки

051000 «Профессиональное обучение», 080200 «Менеджмент»,

190100 «Наземные транспортно-технологические комплексы»,

190700 «Технология транспортных процессов»,

230400 «Информационные системы и технологии»,

270800 «Строительство», 280700 «Техносферная безопасность»

Семенов Иван Петрович, Шабалин Павел Леонидович

5354.ru

Пусть задана бесконечная последовательность чисел

u1,u2 , ,un , .

ЧИСЛОВЫЕРЯДЫ

1. Сумма ряда. Необходимый признак сходимости числового ряда

(1)

Это означает, что задана формула un = f (n) , по которой можно вычислить любое число из этой последовательности по его порядковому номеру. Например, un = (2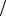n)2 , следовательно, u1 = 4, u2 =1, u3 = 4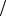9, .

Числовым рядом называется формальная сумма

	∞
u1 +u2 + +un + =	∑un	(2)
	n =1
бесконечного числа слагаемых – членов	последовательности	(1).

Теперь числа un , n =1,∞, будем называть членами ряда (2). Для практической реализации бесконечной операции сложения предложена следующая процедура.

Обозначим символом Sn	сумму первых n слагаемых ряда	(2), т.е.
	n
Sn = u1 +u2 + +un = ∑ui .
	i=1
Величина Sn называется	n −ой частичной суммой ряда (2).
Если существует конечный предел
	S = lim Sn ,	(3)
	n→∞

то число S называют суммой ряда (2), а сам ряд (2) называют схо-

дящимся.

Если Sn при n → ∞ не имеет конечного предела, то ряд (2) называют

расходящимся.

Таким образом, процесс «бесконечного суммирования» заменен нахождением конечной суммы Sn (правда, для любого натурального n ) и предельным переходом в формуле (3). Известным примером сходящегося числового ряда является геометрическая прогрессия со знаменателем q ,

n
\| q \|<1, т.е. числовой ряд вида ∑α qn α −некоторое число. Для n −ой ча-
i=1
- 2 -	5354.ru

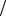
стичной суммы доказана формула Sn =α (1− qn )(1− q) , из которой следует, что в случае, когда | q |<1, предел (3) существует и равен S =α(1− q), т.е. геометрическая прогрессия со знаменателем q, | q |<1, сходится и её сум-

мой является число α (1− q),	если же \| q \|>1, то предел в формуле (3) не
существует, значит при \| q \|>1,	геометрическая прогрессия - расходящийся

ряд.

Отметим, что при нахождении суммы ряда ключевую роль играет нахождение предела в правой части формулы (3). Очень часто этот предел вычислить не удается, поэтому важным является вопрос о том, существует для исследуемого ряда указанный предел или нет, т.е. сходится или расходится этот ряд. Если мы точно знаем, что ряд сходится, то его точную сумму можно заменить на приближенную, взяв несколько первых слагаемых ряда (чем больше, тем ответ точнее). Если же ряд расходится, то у такого ряда суммы не существует, значит и приближенное значение этой суммы находить нельзя. Поэтому весьма важными являются признаки сходимости ряда, по которым было бы нетрудно определить, сходится

данный ряд или нет.
Теорема 1 (необходимый признак	сходимости). Если числовой ряд
(2) сходится, то
limun = 0.	(4)
n→∞

Практически применяется следствие из теоремы 1.

Следствие. Если limun ≠ 0, то ряд (2) расходится.

n→∞

Следствие из теоремы 1 дает достаточный признак расходимости числового ряда. Именно, если для некоторого числового ряда условие (4) не выполнено, то этот ряд расходится.

Пример.

На основании следствия из теоремы 1 легко установить, что геомет-

рическая прогрессия ∑∞n=1αqn ,	в случае	\| q \|≥1 является расходящимся ря-
дом. Действительно,
limun = lim aqn = a lim qn = ∞,
n→∞	n→∞	n→∞

т.е. limun ≠ 0, следовательно, в этом случае геометрическая прогрес-

n→∞

сия является расходящимся рядом.

- 3 -

5354.ru

Подчеркнем, что при помощи необходимого признака сходимости

можно установить лишь расходимость ряда: если limun ≠ 0, то ряд расхо-

n→∞

дится. Если же оказалось, что limun = 0, то эта информация нам ничего не

n→∞

дает: ряд может оказаться как сходящимся, так и расходящимся.

1. Ряды с положительнымичленами.Признакисравнения

Будем рассматривать ряд (2), все члены которого положительны, т.е. un > 0, n =1,∞. Такие ряды называются знакоположительными. Для исследования сходимости знакоположительного ряда часто оказываются полезными следующие признаки.

Теорема 2 (первый признак сравнения). Даны два знакоположи-

тельных ряда ∑α qn

i=1

∑∞n=1vn , причем для каждого порядкового номера n выполнено неравенство un < vn , n =1,∞. Тогда если ряд ∑∞n=1vn сходится, то и ряд ∑∞n=1un , сходится, если ряд∑∞n=1un , расходится, то и ряд ∑∞n=1vn расходится.

Теорема 3 (второй признак сравнения). Даны два знакоположи-

тельных ряда	∞	u	,	∞ v	n	. Если существует предел	limu	n	v	n	= a ,
	∑n=1	n		∑n=1	n		n→∞	n		n

0 < a < ∞ , то оба ряда или сходятся, или оба расходятся.

Для того, чтобы применять признаки сравнения для исследования сходимости числового ряда, нужно иметь некоторый набор числовых рядов сходимость или расходимость которых известна. Кроме геометрической прогрессии можно использовать ряд вида

∞	1		1		1		1
∑		=1+		+		+ +		+ ,	(5)
	β		β		β		β
n=1	n		2		3		n

который сходится при β >1 и расходится, если β ≤1. Частный случай ряда (5), который получается из (5) при β =1 называется гармоническим рядом.

Примеры.

1) Исследуем сходимость ряда

sinπ +sin π2 +sin π3 + +sin πn + ,

- 4 -

5354.ru

т.е. un = sin(πn) . В качестве второго ряда выберем гармонический, т.е. vn =1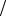n . С использованием первого замечательного предела, учитывая, что при n → ∞ число π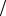n → 0 , вычислим предел

a = lim un	= lim sin(π n)		=π lim sin(π n)		=π, 0 <π < ∞.
i→∞ v	n→∞	1 n	i→∞	π n
n

Следовательно, по второму признаку сравнения оба ряда ведут себя одинаково, а так как гармонический ряд расходится, то и исследуемый ряд

∞

∑sin(π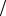n) так же расходится.

n=1

2) Исследуем сходимость ряда

+ +

+ .

125

(2 + n)n

Здесь

=1 (2 + n)n ,

выберем

vn = (1 2)n . Ряд с общим члено

vn = (1 2)n является геометрической прогрессией с

α =1 и знаменателем

q =1 2 <1, т.е. является сходящимся рядом. Поскольку для

n =1,2,3,

справедливо

неравенство

2 + n > 2,

то

1 n

n =1,∞.

< = vn ,

2 + n

+ n

Итак, доказали,

что для всех целых положительных

n выполнено

неравенство

un < vn . По первому признаку сравнения (теорема 2)

ряд

∑∞n=1un = ∑∞n=11(2 + n)n сходится.

2. ПризнакиДаламбера иКоши

Рассмотрим ряд с положительными членами ∑∞n=1un .

Теорема 4 (признак Даламбера). Пусть существует конечный пре-

дел l = lim un+1 .

n→∞ un

Тогда при l <1 ряд сходится, при l >1 ряд расходится.

Пример.

Исследуем ряд

∑∞n=1 2n n . Здесь un = 2n n , следовательно,

un+1 = 2n+1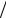(n +1) . Вычислим предел

l = lim un+1	= lim	2n+1 n	= 2 lim	n	= 2 lim	1	= 2 >1,
						1+1 n
n→∞ un	n→∞ (n +1)2n		n→∞ n +1		n→∞
			- 5 -				5354.ru

Следовательно, исследуемый ряд расходится.

Теорема 5 (радикальный признак Коши). Пусть существует конеч-

ный предел l = lim n un . Тогда при l <1 ряд сходится, при l >1 ряд расхо-

n→∞

дится.

Пример.

<1.

un =

, l

= lim n

un = lim

= lim

3n + 2

n→∞

n→∞ 3n + 2

n→∞ 3 + 2 n

Ряд сходится.

Теорема 6 (интегральный признак Коши). Дан знакоположитель-

ный ряд ∑∞n=1un , причем

u1 ≥ u2 ≥ ≥ un

≥ un+1 ≥ .

(6)

Пусть f (x) −непрерывная, монотонно убывающая функция такая,

что f (1) = u1, f (2) = u2 , ,

f (n) = un , .

Тогда, если несобственный интеграл

∫a∞ f (x)dx сходится,

то и ряд

∑∞n=1un

сходится, если несобственный инте-

грал

∫a∞ f (x)dx

расходится, то и ряд

∑∞n=1un

расходится (здесь выбранное

нами положительное число).

Пример.

При помощи этого признака исследуем ряд (5) в котором

un =1 nβ ,

β > 0 . Очевидно, что u1 =1 > u2

=1 2β

> u3 =1 3β

> > un =1 nβ

> ,

т.е. условие

(6) выполнено. Определим функцию f (x)

формулой f (x) =1 xβ . Очевидно,

что функция

f (x)

непрерывна и монотонно убывает на интервале [1,+∞).

Рассмотрим теперь в случае β ≠1 несобственный интеграл

∞ dx =

lim

M dx

= lim

x1−β

M = lim

M 1−β −

∫

M →∞

1− β

M →∞

1− β

1 x

1− β

Теперь ясно, что если

β >1,

то

M 1−β → 0 при

M → ∞ и несоб-

ственный интеграл

∞ dx

∫1 xβ

= −

1− β

β −1

т.е. сходится. По теореме 6 ряд (5)

при β >1

сходится. Если

β <1, то

M 1−β

→ ∞ при

M → ∞ ,

следовательно,

несобственный

интеграл

∫1∞ x−β dx

- 6 -

5354.ru

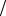
расходится, согласно интегральному признаку Коши ряд (5) так же расходится. Наконец в случае β =1 имеем

∞ dx	= lim M dx	= lim ln x	M	= lim [ln M −ln1]= ∞,

∫1 x	M →∞ ∫1 x	M →∞	1	M →∞

Т.е. интеграл, а значит, по теореме 6 и гармонический ряд расходятся. Итак, ряд (5) сходится при β >1 и расходится при β ≤1.

3. Знакочередующиеся ряды, теорема Лейбница

Рассмотрим теперь числовой ряд, знаки членов которого чередуются

∞
u1 −u2 +u3 − +(−1)n+1un + = ∑(−1)n+1un ,	un ≥ 0.	(7)

n =1

Такой ряд называется знакочередующимся. Можно показать, что если ряд, составленный из абсолютных величин членов рядя (7), т.е. ряд u1 +u2 + +un + сходится, то и сам знакочередующийся ряд (7) сходится. В этом случае говорят, что ряд (7) сходится абсолютно. Если ряд, составленный из абсолютных величин членов ряда (7) расходится, а сам знакочередующийся ряд (7) все же сходится, то говорят, что ряд (7) сходится условно. Условная сходимость ряда (7) может быть установлена при помощи следующего достаточного признака сходимости знакочередующихся рядов.

Теорема 7 (Лейбниц). Если для знакочередующегося ряда (7) выполнены условия

u1 ≥ u2 ≥ ≥ un ≥ un+1 ≥ ,	(8)
limun = 0,	(9)
n→∞

то ряд (7) сходится и сумма ряда будет положительным числом меньшим u1 .

Пример.

Дан знакочередующийся ряд

1− 12 + 13 − 14 + + (−1)n+1 1n + ,

т.е. un =1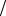n . Проверим для этого ряда выполнение условий теоремы 7. Очевидно, что u1 =1 > u2 =1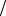2 > u3 =1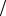3 > > un =1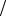n > , т.е. условие (8) вы-

полнено; так как lim1 n = 0, то условие (9) выполнено, следовательно, ис-
n→∞
- 7 -	5354.ru

x, x > R .

следуемый ряд сходится, причем условно. Последнее вытекает из того, что ряд, составленный из абсолютных величин членов знакочередующегося ряда, является гармоническим, т.е. расходящимся.

ФУНКЦИОНАЛЬНЫЕРЯДЫ

4.Степенныеряды,область сходимости степенного ряда

Ряд

∞

u1(x) +u2 (x) + +un (x) + = ∑un (x)

n =1

члены которого являются функциями переменной x , называются функциональным. При каждом значении x этот ряд будет представлять собой числовой ряд, который либо сходится, либо расходится.

Множество всех значений x , для которых получившийся из функционального ряда числовой ряд сходится, называется областью сходимости данного функционального ряда.

Очевидно, что для всех значений x из области сходимости сумма функционального ряда существует и является некоторой функцией переменной x .

Степенной ряд является частным случаем функционального ряда и имеет вид

	∞
a0 + a1x + a2 x2 + + an xn + = ∑an xn		(10)
	n =0
(это степенной ряд по степеням x ) или
	∞
a0 + a1(x − x0 ) + a2 (x − x0 )2	+ + an (x − x0 )n + = ∑an (x − x0 )n	(11)

n =0

(степенной ряд по степеням (x − x0 ) ). Здесь x0 , a0 , a1, a2 , ,an , −заданные числа, a0 , a1, a2 , ,an , называются коэффициентами степенного ряда.

Положительное число R называется радиусом сходимости степенного ряда (10), если этот ряд абсолютно сходится для всех x, x < R , и расходится для всех

- 8 -

5354.ru

Положительное число R называется радиусом сходимости степен-
ного ряда лиэтот ряд абсолютно сходится для всех x,				x − x0	< R, и расхо-

дится для всех x,	x − x0		> R .

Областью сходимости степенного ряда является интервал сходимо-
сти. Для ряда
(10) это интервал (−R, R) , а для степенного ряда (11) – интервал
(x0 − R, x0 + R) . На концах интервала сходимости (в точках x = −R, x = R для
ряда (10) и в точках		x = x0 − R , x = x0 + R для ряда (11)) степенной ряд мо-

жет сходиться, а может и расходиться. Этот вопрос исследуется отдельно. Радиус сходимости степенного ряда определяется по формуле

R =

где

L = lim

an+1

или

L = lim n

Примеры.

n→∞

Найти интервал сходимости следующих степенных рядов

∞

∑

(−x)

здесь

an =

(−1)

an+1

n−1

n +1

n=1 3

an+1

3n−1

L = lim

= lim

= 3 . Для данного ряда интервал сходимо-

n→∞

3n n +1

сти (−3,3) .

∞

(x + 2)

2) ∑

здесь

n=1

n+1

(n +1)2

= lim

(n +1)2

(1+1 n)2

n→∞

следовательно,

R =1,

так

как

x0 = −2, то

интервал сходимости

(−2 −1,−2 +1),

т.е. (−3,−1) .

Ряды Тейлора иМаклорена

Дана функция

y = f (x) ,

которая имеет непрерывные производные

любого порядка

в некоторой

окрестности

точки

x0 . Найдем числа

f (x0 ), f ′(x0 ),

f ′′(x0 ), f (n) (x0 ),

с использованием которых образуем сте-

пенной ряд по степеням

(x − x0 )

вида

- 9 -

5354.ru

f (x0 ) +		f ′(x0 )	(x − x0 ) +	f ′′(x0 )	(x − x0 )2 + +		f (n) (x0 )	(x − x0 )n +	(12)


	1!
			2!				n!
Этот	ряд,		построенный с			использованием значений функции
y = f (x) и её производных в точке						x0 , называется рядом Тейлора функ-
ции f (x) . Поскольку мы знаем коэффициенты этого ряда an									= f (n) (x0 ) n!,
то можем вычислить радиус сходимости данного ряда R =1 L									и записать
интервал сходимости (x0 − R, x0 + R) .						Ряд (12) в каждой точке x			своего ин-

тервала сходимости будет сходиться к функции f (x) , по которой этот ряд был построен (т.е. иметь своей суммой функцию f (x) ), если выполнено условие


			lim		f (n+1) (ζ )	(x − x0 )n+1			= 0	(13)
			lim			(x − x0 )n+1			= 0	(13)
			n→∞		(n +1)!
для всех	x из интервала сходимости. Здесь								ζ −некоторая точка, разделя-
ющая x	и	x0 . Итак, если выполнено условие (13), то для всех
x (x0 − R, x0 + R)		имеет место условное равенство
	f (x) = f (x0 ) +		f ′(x0 )		(x − x0 ) +		f ′′(x0 )	(x − x0 )2 + +		f (n) (x0 )	(x − x0 )n + .
	f (x) = f (x0 ) +				(x − x0 ) +			(x − x0 )2 + +			(x − x0 )n + .
		1!		2!						n!
Здесь	R −радиус сходимости ряда (12). В этом случае говорят, что
функция	y = f (x) представима своим рядом Тейлора. Если же условие (13)

не выполнено, то внутри своего интервала сходимости ряд (12) будет сходиться, но его суммой будет не функция f (x) .

При x0 = 0 ряд Тейлора для функции y = f (x) принимает вид

f (0) +

f ′(0)

x +

f ′′(0)

x2 + +

f (n) (0)

xn +

и называется рядом Маклорена. Этот ряд в каждой точке x

своего

интервала сходимости (−R, R) , где

R −радиус сходимости ряда,

будет

сходиться к функции f (x) ,

т.е. будет иметь место условное равенство

f (x) = f (0) +

f ′(0)

x +

f ′′(0)

x2 + +

f (n) (0)

+ ,

если выполнено соотношение

lim

f (n+1) (ζ )

xn+1 = 0 ,

(14)

n→∞

(n +1)!

где ζ − некоторая точка, разделяющая x

и начало координат.

- 10 -

5354.ru

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.05.2015150.53 Кб5rgr_PM_bakalavriat.doc
#
24.04.2019125.44 Кб1RTsB_test.doc
#
12.05.2015371.27 Кб10rulturologiy 2.pdf
#
14.11.2018293.89 Кб4russkij-yaz.-egye-chast-s-yenciklopediya.doc
#
17.03.2016150.23 Кб8rutrvar56.pdf
#
17.03.2016311.15 Кб4ryady_metod_ukazaniya_kgasu_5354.pdf
#
12.05.20153.88 Mб42SalimovRB_matematika_gl_1-20_2011_web.pdf
#
12.05.20153.69 Mб71SalimovRB_matematika_gl_1-9_2011_web.pdf
#
11.05.2015988.67 Кб44Sbornik_testov_s_otvetami_marketing.doc
#
12.05.20159.79 Mб13SGH_i900_service_manual-spaces_ru.pdf
#
12.05.2015526.35 Кб48Shavali_Burova_109_13.pdf