
SalimovRB_matematika_gl_1-20_2011_web
.pdfи проходящими через точки a, b оси Ox ). Кривые APB, AQB области D, заданные соответственно уравнениями
Здесь a, b – абсциссы точек A, B границы области D. Будем считать, что функции 1 x , 2 x однозначны. Это означает, что любая прямая, параллельная Oy и проходящая через точку x интервала a, b , пересекает линию а также линию AQB только в одной точке, причём – ордината P – точки входа этой прямой в область D, 2 x – ордината Q – точки выхода этой прямой из области D. Ясно, что по этой прямой плоскость Oxy пересекает плоскость, перпендикулярную к Ox и проходящую через точку x. Эта плоскость пересекает рассматриваемое цилиндрическое тело по фигуреPMNQ , представляющей собой криволинейную трапецию с основанием PQ. Сверху трапеция ограничена кривой MN. Все точки указанной плоскости, следовательно, и кривой MN , имеют одну и ту же абсциссу x . Но так как кривая MN лежит на поверхности z f x, y , то координаты точек этой кривой удовлетворяют уравнению z f x, y поверхности. У всех точек кривой MN абсцисса не изменяется, а изменяется ордината y от значения 1 x – ординаты точки P, до значения 2 x – ординаты точки Q.
Итак, кривая MN , ограничивающая сверху криволинейную трапецию имеет уравнение z f x, y , x const, 1 x y 2 x . Теперь площадь S этой трапеции PMNQ можем вычислить с помощью определённого инте-
грала, а именно,
2 x
S f x, y dy, x const .
1 x
Ясно, что для различных фиксированных x из интервала a, b эта
площадь будет различной, так как будут различаться соответствующие криволинейные трапеции, т. е. эта площадь есть функция от x. Обозначим её S x . Таким образом,
S x |
2 x |
f x, y dy, |
(9) |
|
1 x
где a x b.
241
5354.ru

Итак, для каждого x из a, b известна площадь S x сечения цилиндри-
ческого тела плоскостью, проходящей через точку x перпендикулярно к оси Ox. Мы знаем, что объём V рассматриваемого цилиндрического тела выражается с помощью определённого интеграла, взятого от a до b для функции
S x , т. е. V ab S(x)dx. Вместо S x |
подставим сюда выражение (9) и получим |
|||
b 2 |
x |
|
||
V |
|
|
f x, y dy dx. |
|
a |
|
x |
|
|
|
1 |
|
|
|
Но с другой стороны найденный объём V |
|
согласно (8) равен двойному инте- |
|||
гралу, поэтому |
|
|
|
|
|
|
b 2 |
x |
|
||
f x, y dxdy |
|
|
f x, y dy dx. |
||
D |
a |
1 |
x |
|
|
|
|
|
|
||
Выражение в правой части называется двукратным интегралом. Последнюю формулу можно записать в более простой форме
|
b |
2 x |
|
|
f x, y dxdy dx |
|
f x, y dy. |
(10) |
|
D |
a |
1 x |
|
|
Таким образом, (10) – формула вычисления двойного интеграла. Здесь в правой части внутренний интеграл берется по y при постоянном x .
Формула (10) справедлива и тогда, когда граница области D имеет участки, лежащие на прямых x a, x b (или на других прямых, параллельных оси Oy ), т. е. когда область D имеет вид, указанный на рис. 133.
Рис. 133
Если в последнем случае 1 x c const и 2 x d const, то область D имеет форму прямоугольника, стороны которого параллельны координатным
242
5354.ru

осям. В этом случае пределы внутреннего интеграла правой части (10) – пределы для y – также будут постоянными.
|
Рис. 134 |
|
Пусть теперь область D |
расположена между прямыми y c, |
y d и |
участки её границы CAD1, CBD1 |
заданы соответственно уравнениями x 1 y , |
|
x 2 y , |
в которых c y d (рис. 134). В этом случае, как и при выводе фор- |
|||
мулы (10), покажем, что имеет место формула, аналогичная (10): |
|
|||
|
|
d |
2 y |
|
|
f x, y dxdy dy f x, y dx. |
(11) |
||
|
D |
c |
1 y |
|
Здесь справа внутренний интеграл по x берется при постоянном y.
Левые части формул (10) и (11) равны, следовательно, равны их правые части. Приравняв их, получим
d |
2 y |
b |
2 x |
|
dy |
f x, y dx dx |
f x, y dy. |
||
c |
1 y |
a |
1 x |
|
Отметим, что последнее соотношение есть формула перестановки интегралов в двукратном интеграле.
Если область D имеет более общий вид, чем указано выше, и может быть разбита на части, для которых справ едливы формулы (10) или (11), то двойной интеграл по исходной области будет равен сумме двойных интегралов по указанным её частям.
243
5354.ru
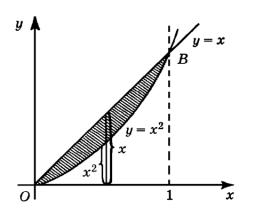
Пример. |
Вычислить |
x2 y dxdy, |
|
||
|
|
|
D |
|
|
где D – конечная область, лежащая меж- |
|
||||
ду параболой |
y x2 |
и |
прямой |
y x |
|
(рис. 135). Эти кривые пересекаются в |
|
||||
точках O 0, 0 |
и B 1, 1 . Область D – за- |
|
|||
штрихованная область. Она расположена |
|
||||
между прямыми x 0 |
и |
x 1, следова- |
|
||
тельно, в нашем случае a 0, b 1. |
С одной |
Рис. 135 |
|||
стороны область ограничена кривой y x2 , |
с другой – прямой y x. Правые |
||||
части этих уравнений суть пределы внутреннего интеграла формулы (10), т. е.1 x x2 , 2 x x. При фиксированном x эти величины означают соответ-
ственно ординаты точки входа и точки выхода из области D прямой, прохо-
дящей через точку x параллельно оси Oy. |
Итак, в рассматриваемом примере |
||
формула (10) даёт |
|
|
|
x2 |
1 |
x |
x2 y dy. |
y dxdy dx |
|||
D |
0 |
x2 |
|
Сначала вычислим внутренний интеграл по y при x const . Он является обычным определённым интегралом, поэтому вычислим его по формуле Ньютона–Лейбница:
|
2 |
1 |
|
2 |
|
y2 |
|
y x |
1 |
|
|
3 |
|
x2 |
|
4 |
|
x4 |
|
|
|||
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
y dxdy dx x |
|
y |
|
|
|
|
dx x |
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
2 |
|
2 |
|||||||||||||||||
D |
|
0 |
|
|
|
2 |
|
y x2 |
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 3x4 / 2 x3 x2 / 2)dx 3x5 |
/10 x4 |
/ 4 x3 |
/ 6 |
|
10 |
7 / 60. |
|
||||||||||||||||
|
|
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предлагаем самостоятельно вычислить данный двойной интеграл, используя формулу (11).
§8. Замена переменных в двойном интеграле
Вдекартовой системе координат Oxy на плоскости дана область D , ограниченная кривой L , и P x, y – некоторая точка этой области (рис. 136).
244
5354.ru

Рис. 136 |
Рис. 137 |
|
|
– область, |
Пусть O uv – другая декартова система координат, в ней |
D |
|
||
|
|
|
||
|
|
|
||
ограниченная кривой L', и P u, v – некоторая точка области D (рис. 137). Пусть заданы две функции
x u, v , y u, v , (12)
которые будем считать непрерывными и имеющими непрерывные частныепроизводные первого порядка как по u, так и по v всюду в области D . Предположим, что функции (12) таковы, что каждой точке P u, v области D они
ставят в соответствие определённую точку P x, y области D (зная координаты u, v точкиP , по формулам (12) найдем координаты x, y соответствующей точки P областиD ). И наоборот, каждой точке P x, y области D отвечает определённая точка P с координатами u, v области D (зная координаты x, y точкиP , из соотношений (12) найдем координаты u, v соответствующей точки P областиD ). В этом случае говорят, что формулы (12) устанавливают взаимнооднозначное соответствие между точками области D с одной стороны и точками области D с другой. Или ещё говорят, что эти функции отображают область D на область D. От функций (12) вычислим частные производные по u и v и образуем определитель из найденных частных производных, обозначаемый J и равный
J |
|
x / u |
x / v |
|
. |
(13) |
|
|
|||||
|
|
y / u |
y / v |
|
|
|
Он называется определителем Якоби для функций (12).
Без доказательства запишем формулу замены переменных в двойном интеграле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14) |
D |
f |
|
x, y |
|
dxdy |
D |
f |
|
u, v |
|
, |
|
u, v |
|
|
J |
dudv. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
245 |
|
|
|
|
|
|
|
|
|
|
|
|
5354.ru |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Таким образом, при замене переменных по формулам (12) в двойном интеграле по области D мы должны переменные интегрирования x, y заменить соответственно на u, v , u, v , а элемент площади dxdy – на J dudv (причём двойной интеграл в правой части берётся по новой областиD ).
§9. Переход в двойном интеграле к полярным координатам
Вкачестве примера замены переменных в двойном интеграле рассмотрим переход в двойном интеграле к полярным координатам. Пусть в декартовой системе координат Oxy задана область D, ограниченная кривой L. В плоско-
сти Oxy кроме декартовой введём полярную систему координат, поместив полюс в точку O и направив полярную ось по Ox в положительном направле-
нии (рис. 138). Пусть x, y – декартовы координаты точки M области D, |
а |
и – полярные координаты этой точки. Как видно из рис. 138, |
|
x cos ; y sin . |
(15) |
Рис. 138
Пусть граница области D задана уравнениями в полярных координатах, а именно, участок APB кривой L задан уравнением 1 , , а уча-
сток AQB кривой L – уравнением 2 , . Отметим, что уравне-
ние определяет осьOA, а уравнение |
соответственно ось OB. Отме- |
|
тим также, |
что при фиксированном 1 |
есть расстояние OP, а 2 – |
расстояние |
OQ. Введем ещё одну декартову систему O . В этой системе |
|
|
|
|
, уже декартовы координаты точки плоскости O , в то время как в плос- |
||
|
|
|
кости Oxy |
они являются полярными координатами соответствующей точки. |
|
По формулам (15) каждой точке области D будет отвечать точка области D в
246
5354.ru
плоскости O , и тем самым в этой плоскости получим область D с границей L', в которую переходит область D плоскости Oxy (рис. 139).
|
Уравнения и |
Рис. 139 |
|
|
определяют прямые, |
парал- |
|||||||||||||||||
|
в плоскости O |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ясно, что |
|||
лельные оси O . Между этими прямыми расположена область D . |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
отвечает участок A P B |
|
кривой |
||||||||||||||
участку APB кривой L с уравнением 1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L ' |
с тем же уравнением 1 , так как полярные координаты точки линии |
||||||||||||||||||||||
L |
являются декартовыми координатами соответствующей точки кривой L . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линии AQB отвечает часть |
A Q B |
|
кривой |
L' |
с |
уравнением |
|
2 |
|
|
. Для |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функций (15) вычислим определитель Якоби (13), положив в нём u , |
v : |
||||||||||||||||||||||
|
|
|
|
|
J |
|
x / |
x / |
|
|
|
sin |
cos |
|
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
y / |
y / |
|
|
|
cos |
sin |
|
|
|
|
|
|
|
|
||
Таким образом, |
|
J |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Запишем формулу (14) для нашего случая (когда вместо функций (12) бе- |
||||||||||||||||||||||
рутся функции (15)): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
f x, y dxdy f cos , sin d d . |
|
|
|
|
(16) |
|||||||||||
|
|
|
|
|
|
|
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
Это есть формула перехода в двойном интеграле к полярным координатам,
здесь D – область в декартовой системеO . Теперь двойной интеграл по этой области D выразим через двукратный, использовав формулу (10). Получим
|
|
2 |
f cos , sin d . |
|
f x, y dxdy d |
|
(17) |
||
D |
|
1 |
|
|
247
5354.ru

Формула (17) справедлива и тогда, когда граница L области D имеет участки, лежащие на прямых , , т. е. когда область D имеет вид, представленный на рис. 140.
Рис. 140
Если в последнем случае 1 0, то область D принимает вид сектора (рис. 141). Для этого сектора в формуле (17) нужно взять 1 0.
Рис. 141
Пусть в последнем случае a 0, а 2 , при этом область D имеет вид, изображенный на рис. 142.
Рис. 142
Для этой области в формуле (17) нужно взять a 0, 2 , 1 0.
248
5354.ru

Пусть в последнем случае 2 R const, тогда область D имеет форму круга с центром в начале координат и радиусом r R (рис. 143).
Из сказанного выше ясно, что для этого круга в формуле (17) мы должны взять a 0, 2 , 1 0, 2 R. Поэтому на практике при вычислении
двойного интеграла по области в виде круга лучше перейти к полярным координатам указанным выше способом.
Отметим, что пределы двукратного интеграла формулы (17) устанавливаются непосредственно по уравнениям в полярных координатах частей границы L области D.
§ 10. Вычисление площади поверхности с помощью двойного интеграла
Пусть в области D на плоскости Oxy задана функция z f x, y . Будем
считать, что эта функция имеет непрерывные частные производные по x и по y в области D. Для определённости предположим, что f x, y 0 в D. При
этом в пространстве Oxyz функции z f x, y отвечает поверхность, расположенная выше плоскости Oxy (рис. 144).
Рис. 144
249
5354.ru
Требуется вычислить площадь S этой поверхности.
Разобьём область D на n частей с площадями 1, 2 , ..., n . Внутри части с площадью i возьмём произвольную точку Pi i , i . В этой точке вычислим значение заданной функции z f x, y и найдём число zi f i , i . Это число – аппликата некоторой точки Mi поверхности z f x, y . Очевидно, абсциссы и ординаты точек Mi и Pi совпадают. В точке Mi проведём касательную плоскость к поверхности z f x, y , а через границу области i –
цилиндрическую поверхность с образующими, параллельными оси Oz. Эта поверхность отсечет на только что проведённой касательной плоскости фигуру, площадь которой обозначим Это построение выполним для всех ча-
стей, на которые мы разбили область D , и получим фигуру, состоящую из n кусков касательных плоскостей, проведённых к поверхности z f x, y в точ-
ках M1, M2 , …, Mn . Площадь этой фигуры равна сумме площадей, из кото-
n
рых она состоит, т. е. Si .
i 1
Пусть max di – наибольший из всех диаметров частичных областей i . Число n устремим к бесконечности так, чтобы max di 0. Тогда все i стя-
гиваются в точки, и фигура, состоящая из кусков касательных плоскостей, приближается к заданной поверхности. Поэтому естественно за площадь поверхности S принять предел площади указанной фигуры (состоящей из кусков касательных плоскостей):
|
|
|
n |
(18) |
|
S lim |
Si . |
||
|
max d |
0 |
i 1 |
|
|
i |
|
|
|
Пусть Ni |
есть вектор, направленный по нормали к поверхности z f x, y |
|||
в точке Mi , а i – острый угол, образованный этим вектором с осью Oz. |
Ясно, |
|||
что этот угол равен двугранному углу между касательной плоскостью в точке Mi к рассматриваемой поверхности и плоскостью Поскольку i – про-
екция на плоскость Oxy фигуры с площадью Si , лежащей на указанной касательной плоскости, то
i Si cos i . |
(19) |
Формула (19) очевидна, если Si имеет форму прямоугольника, сторона которого параллельна линии пересечения касательной плоскости в точке Mi к поверхности и плоскости Oxy (сделайте чертёж и убедитесь в этом!). Справед-
250
5354.ru
