SalimovRB_matematika_gl_1-20_2011_web

смотрен пример на построение критерия). Критерий D, естественно, зависит от выборочных значений x1 , x2 , , xn случайной величины и поэтому является случайной величиной. Если закон распределения D известен, то для любого

указанное событие не произойдет в единичном опыте (обычно принимают равным 0,05 или 0,01 и т.д.). Задавшись вероятностью , можно найти D0 D0 ( ) из (28) согласно известному закону распределения величины D. Пусть Dn - фактическое значение критерия D , вычисленное по выборочным данным. Если окажется, что Dn D0 ( ), то мы приходим к выводу, что наша гипотеза опровергнута опытом: в единичном случае произошло событие, вероятность которого очень мала. Если же то будем считать, что гипотеза согласуется с опытными данными. Вероятность называется уровнем значимости. Таким образом, уровень значимости - это вероятность того, что критерий D принимает значения, при которых проверяемая гипотеза отвергается.

Замечание. Отвергаемая гипотеза может оказаться правильной и вероятность является, таким образом, вероятностью, с которой отвергается правильная гипотеза (ошибка первого рода).

Рассмотрим следующую задачу: пусть некоторый эксперимент имеет m элементарных исходов w1 , w2 , , wm . Вероятности этих исходов точно неиз-

вестны, но имеются некоторые основания считать, что они равны p1 , p2 , , pm .

явления события wk в этих испытаниях k 1,2, , m. Относительная частота mnk

появления wk события при больших n согласно теореме Бернулли, близка к неизвестной вероятности, предполагаемое значение которой равно pk . Пирсон показал, что сумма

является подходящей мерой расхождения между наблюденными частотами mnk и гипотетическими вероятностями pk (k 1,2, , m) и обладает замеча-

тельными свойствами: при больших n ее распределение приближенно равно так называемому 2 - распределению (читается: «хи - квадрат» распределению).

Это распределение определяется так. Пусть - независимые

случайные величины с нормальным законом распределения, причем у каждой из них математическое ожидание равно нулю, а среднее квадратическое от-

Справедлива теорема Пирсона. Пусть случайный эксперимент имеет m элементарных исходов wk вероятности которых равны pk , k 1,2, , m. Если в

стремится к 2 -распределению с (m-1) степенями свободы.

Эта теорема (принимаемая без доказательства) лежит в основе статистической проверки гипотезы о том, что та или иная выборка (n наблюдений) является выборкой из совокупности возможных значений некоторой случайной величины X, имеющей данное теоретическое распределение (предполагаемое гипотезой). Величина (29) является критерием проверки гипотезы о законе распределения случайной величины X, а статистический метод проверки этой гипотезы, основанный на использовании суммы m2 1 , называется крите-

рием согласия 2 или критерием Пирсона.

392

5354.ru

При практическом применении критерия Пирсона обычно принимают уровень значимости 0,05 или 0,01 или 0,001. Задавшись уровнем значимости и, зная число степеней свободы m-1 определяем критическое значениеm2 1, такое, что P m2 1 m2 1, . И если фактическое значение критерия m2 1 , вычисленное по формуле (29) (по опытным данным n,m1 , ,mk ) , превосходитm2 1, , то гипотеза отвергается. В противном случае, т. е. если m2 1 m2 1, , гипотеза считается совместимой с опытными данными. При нахождении критического значения m2 1, пользуются специальной таблицей: «критические точки распределения 2 » (Приложение 2)

Пример 1. При 12000 бросаниях монеты Пирсон получил 6019 выпадений герба. Согласуется ли этот результат с гипотезой о том, что вероятность выпадения герба равна 0,5 (при уровне значимости 0,05 )

Решение. При каждом бросании монеты имеются два исхода: w1 {герб},

ми.

Если с помощью критерия Пирсона проверяется гипотеза о том, что случайная величина X имеет данное теоретическое распределение (предполагаемое гипотезой), то поступают следующим образом: некоторый интервал a,b ,

ятность попадания X в интервал lk , которую вычисляют, используя предполагаемое гипотезой теоретическое распределение.

Кроме того, в формулировке теоремы Пирсона заменяется на m2 1 r - распределение с (m-1-r) степенями свободы, где r – число параметров пред-

393

5354.ru

полагаемого распределения. Если предполагаемое распределение является нормальным, то r=2, так как по выборке оценивают два параметра a, .

Пример 2. Из некоторой генеральной совокупности извлечена выборка объёма 200 элементов.

том, что случайная величина в генеральной совокупности распределена по нормальному закону.

Решение. Для вычисления вероятностей pk необходимо вычислить параметры a, , определяющие нормальный закон распределения. Их оценки mx , D X вычислим по выборке на основании формул (13) (14), в которых

xk (xk xk 1 ) / 2, pk* mk / n, n 200, и найдем

тервале ( , ) , то крайние интервалы в ряде распределения заменим на ( ,6) и [20, ) . Имеем

0,3389 0,0818.

Аналогично

394

5354.ru

Определим число степеней свободы. По выборке определены два пара-

нований отвергнуть гипотезу о том, что генеральная совокупность, из которой извлечена выборка, имеет нормальный закон распределения.

395

5354.ru

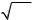
ПРИЛОЖЕНИЕ 1. ЗНАЧЕНИЯ ФУНКЦИИ

397

5354.ru

ПРИЛОЖЕНИЕ 2. КРИТИЧЕСКИЕ ТОЧКИ РАСПРЕДЕЛЕНИЯ c2

398

5354.ru

ЛИТЕРАТУРА

1.Берман А.Ф., Араманович И.Г. Краткий курс математического анализа. Для втузов. – М.: Наука, 1973. – 720 с.

2.Бугров Я.С., Никольский С.М. Высшая математика, т. 1.: Элементы линейной алгебры и аналитической геометрии. – М.: Дрофа, 2003. – 285 с.

3.Бугров Я.С., Никольский С.М. Высшая математика, т. 2.: Дифференциальное и интегральное исчисление.– М.: Дрофа, 2003. – 509 с.

4.Бугров Я.С., Никольский С.М. Высшая математика, т. 3.: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного пере-

менного.– М.: Дрофа, 2003. – 511 с.

5.Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные при-

ложения. – М.: Наука, 1988. – 480 с.

6.Гмурман В.Е. Теория вероятностей и математическая статистика. - М.:

Высш. шк., 2004. – 479 с.

7.Пискунов Н.С. Дифференциальное и интегральное исчисления. Для вту-

зов, т. 1. – М.: «Интеграл-пресс», 2001. – 416 с.

8.Пискунов Н.С. Дифференциальное и интегральное исчисления. Для вту-

зов, т. 2. – М.: «Интеграл-пресс», 2001. – 544 с.

9.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления,

т. 1. - М.: Физматлит, 2003. – 679 с.

10.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления,

т. 2. - М.: Физматлит, 2003. – 864 с.

11.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления,

т. 3. - М.: Физматлит, 2003. – 728 с.

12. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей матема-

тики, т. 1. – М.: Высш. шк., 1978. – 384 с.

13.Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей матема-

тики, т. 2. – М.: Высш. шк., 1978. – 328 с.

399

5354.ru