
SalimovRB_matematika_gl_1-20_2011_web
.pdfчто левая часть – сложная функция, в которой F – функция трёх переменных. Поэтому
|
|
|
|
|
|
|
|
|
|
F |
xt F yt |
F zt |
0. |
(42) |
|
|
|
|
|
|
|
|
|
|
x |
y |
z |
|
|
Соотношение (42) справедливо для любой точки линии L и в том числе для |
||||||||||||||
значения t, отвечающего точке P. |
Возьмём скалярное произведение векторов |
|||||||||||||
N и r t , |
построенных в точке P. |
Оно равно сумме произведений одноимён- |
||||||||||||
ных |
|
проекций |
|
соответствующих |
векторов |
N |
и |
r (t) : |
||||||
|
|
|
|
F |
|
F |
|
F |
|
В силу (42) правая часть последней форму- |
||||
|
||||||||||||||
N, r |
|
(t) |
x |
x (t) |
y |
y (t) |
z |
z (t). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
лы равна нулю. Итак, скалярное произведение (N , r (t)) 0, а поскольку длины
векторов не равны нулю - векторы перпендикулярны. Итак, N r t , |
но L – |
любая кривая, лежащая на поверхности и проходящая через точку P. |
Таким |
образом, любая касательная прямая к поверхности перпендикулярна векторуN. Это означает, что все касательные прямые к поверхности в точке P перпендикулярны N – одному и тому же вектору. Следовательно, все касательные прямые лежат в одной плоскости. Теорема доказана.
Указанная плоскость называется касательной плоскостью к поверхности в точке P. Мы показали, что вектор N с началом в точке P, проекции которого F / x, F / y, F / z суть частные производные, вычисленные в точке P,
есть вектор, перпендикулярный к касательной плоскости поверхности в точке P, т. е. является нормальным вектором этой плоскости.
Прямая, проходящая через точку P и перпендикулярная к касательной плоскости в ней, называется нормалью к поверхности в точке P.
§18. Уравнение касательной плоскости и нормали
кповерхности
Пусть поверхность задана уравнением (39) и P0 x0 , y0 , z0 – фиксированная точка этой поверхности, т. е. её координаты x0 , y0 , z0 – заданные числа. Вычислим частные производные F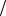 x , F
x , F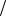 y , F
y , F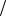 z и найдём их значения в точке
z и найдём их значения в точке
P0 :
181
5354.ru
|
F |
|
F |
|
|
|
|
F |
|
|
F |
|
|
|
F |
|
F |
|
x x . |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x x |
, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
x P |
|
x |
|
y y0 |
|
|
y |
P |
|
y |
x x0 |
|
|
z P |
|
z |
|
y y0 |
|
0 |
|
0 |
|
|
|
|
|
y y |
|
|
0 |
|
0 |
|||||
|
|
|
|
|
z z0 |
|
|
|
0 |
|
|
z z00 |
|
|
|
|
|
|
z z0 |
Получили определённые числа, которые являются проекциями нормального
вектора |
|
|
F |
|
|
F |
, |
F |
|
|
|
касательной плоскости к поверхности в |
||||||||||
N |
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
P0 |
|
y P |
|
z |
P0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точке P0 . |
Зная проекции этого вектора и координаты x0 , y0 , z0 |
точки P0 , сразу |
||||||||||||||||||||
запишем уравнение касательной плоскости: |
|
|
|
|
||||||||||||||||||
|
|
|
|
F |
x x |
|
F |
y y |
|
F |
z z 0. |
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
x P0 |
|
|
|
y P |
|
|
z P0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Зная координаты точки P |
и проекции вектора N |
для точки P , являющегося |
||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
направляющим вектором нормали к поверхности в точке P0 , |
запишем кано- |
|||||||||||||||||||||
нические уравнения этой нормали |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
y y0 |
|
|
z z0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
F x P |
F y P |
F z P |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
В качестве примера возьмём сферу с центром в начале координат и урав-
нением x2 y2 |
z2 3 0. В точке P 1, 1, 1 сферы запишем уравнение касатель- |
|||||||||||||
ной плоскости и уравнение нормали. Итак, x0 1, |
|
y0 1, |
z0 1. |
|
||||||||||
|
F |
2x |
|
|
F |
|
|
|
|
F |
2z |
|
|
2. |
|
|
|
|
|
|
|||||||||
|
|
|
x x0 2, |
|
2y |
|
y y0 2, |
|
|
|
z z0 |
|||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
x P0 |
|
|
|
y P |
|
|
|
|
z P0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Решение данной задачи до конца предлагается довести самостоятельно.
§ 19. Производная по направлению
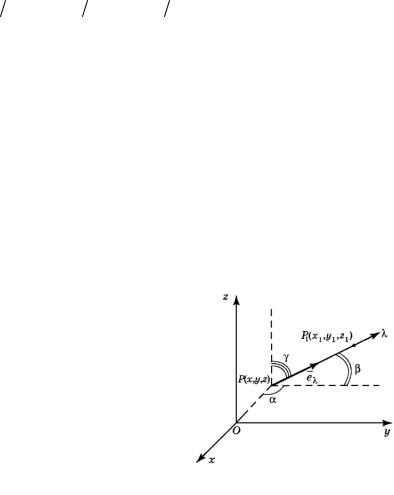
Пусть в системе координат Oxyz задано скалярное поле, т. е. функция трёх переменных U P U x, y, z , и P x, y, z – произвольная точка пространства. Проведем через нее ось , направ-
ление которой определяется единичным вектором e (см. рис. 99). Пусть ось образует с ося-
ми координат Ox, |
Oy, Oz углы , |
соответ- |
ственно, тогда |
e cos cos , cos . |
Пусть |
P1 x1 , y1 , z1 – произвольная точка оси , а расстояние
182
Рис. 99
PP1 Проекции векто-
5354.ru

ра PP1 на оси координат равны разностям координат конца и начала этого вектора:
|
( x1 x, y1 y, z1 z). |
(43) |
PP1 |
С другой стороны, проекции этого вектора равны его длине умноженной
на |
косинус |
угла между |
соответствующей осью и |
вектором, |
поэтому |
|
cos cos , cos . |
Последние проекции равны соответствующим |
|||
PP1 |
|||||
проекциям в (43). Таким образом, |
|
|
|||
|
|
|
x1 cos x, y1 cos y, |
z1 cos z. |
(44) |
Следовательно, с учётом (44) имеем |
|
|
|||
|
|
|
U (P1 ) U (x cos , y cos , z cos ). |
(45) |
|
|
Пусть P |
– фиксированная точка, x, y, z – заданные числа и – фиксиро- |
|||
ванная ось, т. е. , – фиксированные величины. Пусть изменяется только
и точка |
P1 перемещается по оси относительно фиксированной точки P. |
|||||||||||||
При этом, как видно из формулы (45), значение U в точке P1 зависит только |
||||||||||||||
от одной переменной , следовательно, |
отношение [U P1 U P ]/ зависит |
|||||||||||||
только от одной переменной Предел этого отношения при |
0 (когда |
|||||||||||||
P1 P |
по |
оси ) называется производной по направлению |
|
от функции |
||||||||||
U P |
|
U x, y, z в точке |
P |
и обозначается |
U / |
|
U |
x, y, z . |
Итак, производ- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ная по направлению |
|
|
|
|
U P1 U P |
|
|
|
||||||
|
|
|
|
|
U |
lim |
. |
|
(46) |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
Мы знаем, что для полного приращения функции трёх переменных справедливо представление
Ux x, y y, z z U x, y, z
U x U y U z 1 x 2 y 3 z,x y z
где 1, 2 , 3 – бесконечно малые функции, стремящиеся к нулю, когда x 0,y 0, z 0 одновременно. Это представление получено в предположении,
что частные производные U x , U y , |
U z непрерывны. В последней |
формуле положим x cos , y cos , |
z cos . Тогда |
183
5354.ru
|
U (x cos , y cos , z cos ) U (x, y, z) U |
cos |
|
||||
|
|
|
|
|
x |
|
|
|
U cos |
U cos 1 cos 2 cos 3 cos . |
|
||||
|
y |
z |
|
|
|
|
|
Левая часть этой формулы равна U P1 U P . |
Таким образом, получили вы- |
||||||
ражение для U P1 U P . |
Подставим его в числитель формулы (46) и сокра- |
||||||
тим на . |
При этом под знаком предела величины 1, 2 , |
3 стремятся к нулю |
|||||
при 0 |
(когда x 0, |
y 0, |
z 0 одновременно). Тогда (46) даст фор- |
||||
мулу для вычисления производной по направлению в точке P : |
|
||||||
|
|
U |
|
U |
U |
U |
(47) |
|
|
U x, y, z |
x |
cos y cos z cos . |
|||
|
|
|
|
|
|
|
|
Из неё видно, что эта производная зависит от:
координат x, y, z точки P, так как эти координаты входят в выражения для частных производных правой части формулы (47);
направления оси , т. е. от углов , , так как они входят в правую
часть формулы (47).
При фиксированных P и производная по направлению dU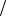 характеризует поведение функции при движении по оси . Когда dU
характеризует поведение функции при движении по оси . Когда dU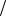 0, в положительном направлении оси функция U возрастает, причём тем быстрее, чем больше эта производная. В сказанном легко убедиться на основании (46).
0, в положительном направлении оси функция U возрастает, причём тем быстрее, чем больше эта производная. В сказанном легко убедиться на основании (46).
§20. Градиент функции и его связь
спроизводной по направлению
Пусть в пространстве Oxyz задано скалярное поле, т. е. функция U P U x, y, z , где x, y, z – координаты точки P. От этой функции найдём частные производные U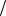 x , U
x , U 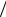 y , U
y , U 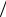 z. Эти производные вычислим для точки P x, y, z и построим вектор с началом в точке P, обозначаемый gradU
z. Эти производные вычислим для точки P x, y, z и построим вектор с началом в точке P, обозначаемый gradU
и называемый градиентом функции в точке P, проекции которого равны только что вычисленным частным производным. Итак, градиент функции U x, y, z в точке P равен
gradU |
U |
|
|
U |
|
U |
|
(48) |
x |
i |
y |
j |
z |
k. |
|||
|
|
|
|
|
|
Длина этого вектора определяется формулой
184
5354.ru

|
|
|gradU | |
|
U 2 |
|
U |
2 |
U 2 |
(49) |
|
|
|
|
|
|
y |
|
|
. |
||
|
|
|
|
x |
|
|
|
z |
|
|
Через точку P проведем ось с единичным вектором |
e |
cos cos , cos |
||||||||
(рис. 100). Запишем скалярное произведение векторов e |
и |
|
|
|||||||
gradU : |
|
|
|
|
|
|
|
|
|
|
gradU, e U |
cos U |
cos U |
cos . |
|
|
|
|
|
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
Правая часть этой формулы равна U |
– производной |
|
Рис. 100 |
|||||||
по направлению от функции U |
в точке P. Таким обра- |
|
||||||||
|
|
|||||||||
зом, получим |
|
|
|
gradU , e . |
|
|
|
|||
|
|
U |
|
|
(50) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Эта формула связывает производную по направлению в точке |
P и gradU в |
|||||||||
точке P. Скалярное произведение в формуле (50) выразим через длины векто- |
||||||||||
ров и косинус угла между ними: |
|
|
|
|
|
|
|
|
||
|
|
U | gradU | cos . |
|
|
(51) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Пусть P – фиксированная точка (её координаты – заданные числа). Тогда gradU в этой точке, определённый по формуле (48), есть фиксированный вектор. Будем изменять угол , т. е. направление оси . Из формулы (51) видно, как изменяется производная по направлению U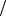 в точке P с изменением направления оси , т. е. угла . Ясно, что наибольшее свое значение эта производная принимает, когда cos 1, т. е. 0, и ось направлена по gradU . Получили, что gradU – вектор, направление которого указывает направление
в точке P с изменением направления оси , т. е. угла . Ясно, что наибольшее свое значение эта производная принимает, когда cos 1, т. е. 0, и ось направлена по gradU . Получили, что gradU – вектор, направление которого указывает направление
наискорейшего возрастания функции |
U по сравнению со всеми другими |
|||||||||
направлениями оси . |
|
|
|
|
|
|
|
|
|
|
Пусть U U x, y, z c, |
где |
c const, |
есть уравне- |
|
|
|
||||
ние поверхности уровня рассматриваемого скалярно- |
|
|
|
|||||||
го поля, проходящей через точку P (рис. 101). Запи- |
|
|
|
|||||||
шем это уравнение так: |
U x, y, z c 0. |
Левую часть |
|
|
|
|||||
обозначим через F x, y, |
z . |
Тогда уравнение этой по- |
|
|
|
|||||
верхности будет |
иметь вид |
F x, y, z 0. |
Частные |
|
|
|
||||
производные от |
функции |
F |
равны |
F |
U |
F |
|
U |
Рис. 101 |
|
x |
x , |
y |
|
y |
, |
|||||
|
|
|
|
185 |
|
|
|
|
5354.ru |
|
|
|
|
|
|
|
|
|
|
|
|
F |
U |
|
|
|
|
|
|
z |
z . Мы знаем, что эти производ-ные, вычисленные в точке P поверхно- |
||||||
сти уровня, являются проекциями вектора N , направленного по нормали к |
|||||||
|
|
|
U |
, U |
, U |
|
Но согласно формуле (48) такие же |
этой поверх-ности, т. е. N |
|
. |
|||||
|
|
|
x |
y |
z |
|
|
проекции имеет и gradU в точке P, |
т. е. |
N |
gradU. Таким образом, gradU есть |
||||
вектор, направленный по нормали к поверхности уровня скалярного поля, проходящей через точку P.
186
5354.ru

ГЛАВА 10. КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Комплексные числа и действия над ними
Комплексным числом называется выражение вида
|
|
|
|
|
|
|
|
z x iy, |
|
|
|
(1) |
где x |
и y |
– действительные числа, i |
– мнимая единица, определяемая равен- |
|||||||||
ством |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
или |
i2 |
1. |
|
(2) |
|
Число |
x |
называется действительной частью, а число |
y |
– мнимой частью |
||||||||
числа z, их обозначают x Re z, y Im z. |
|
|
|
|
|
|
||||||
Два комплексных числа z1 x1 iy1 |
и z2 |
x2 iy2 равны между собой (z1 |
z2 ), |
|||||||||
если x1 x2 , |
y1 y2 . Комплексное число |
z x iy 0, если |
x 0 |
и y 0. |
Два |
|||||||
комплексных числа z x iy и |
|
x iy, |
отличающиеся только знаком мнимой |
|||||||||
z |
||||||||||||
части, называются сопряжёнными. |
|
|
|
|
|
|
|
|||||
Сумма и |
разность. Пусть даны |
два комплексных числа |
z1 x1 iy1 и |
|||||||||
z2 x2 iy2 . Их сумма и разность - комплексные числа, определяемые следующим образом:
z1 z2 x1 x2 i y1 y2 , z1 z2 x1 x2 i y1 y2 .
Произведение z1 z2 – это комплексное число, которое получается при перемножении этих чисел как двучленов по правилам алгебры:
z1 z2 x1 iy1 x2 iy2 x1x2 ix1 y2 iy1x2 i2 y1 y2 ,
или с учётом (2)
z1 z2 x1x2 y1 y2 i x1 y2 y1x2 .
Для |
сопряжённых |
чисел |
z2 x2 iy2 и |
|
x2 iy2 |
|
будем иметь |
z2 z2 |
|||
z2 |
|
||||||||||
x2 |
iy2 x2 iy2 x2 |
2 iy2 2 |
или с учётом (2) |
|
|
|
|
||||
|
|
|
|
|
z2 |
|
x2 |
2 |
y2 |
2 . |
(3) |
|
|
|
|
|
z2 |
||||||
Деление. Для того, чтобы z1 поделить на z2 , нужно числитель и знаменатель дроби z1 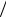 z2 умножить на комплексное число z2 , сопряжённое знаменателю, при этом результатом деления будет комплексное число
z2 умножить на комплексное число z2 , сопряжённое знаменателю, при этом результатом деления будет комплексное число
187
5354.ru

|
z |
|
z |
|
|
|
|
x1 iy1 x2 iy2 |
|
|
|
|
x x ix y |
|
iy x i2 y y |
|
||||||||||||||
|
|
z |
2 |
|
|
2 |
2 |
|||||||||||||||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
1 |
|
1 2 |
1 |
||||||||
|
z |
|
|
z |
|
|
|
|
|
x |
iy |
|
|
x iy |
|
|
|
|
|
x |
2 y 2 |
|
|
|||||||
|
2 |
|
2 |
z |
2 |
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
x1x2 y1 y2 |
|
i |
|
y1x2 x1 y2 |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
x |
2 y |
2 |
|
|
|
|
|
x 2 y 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|||
Пример. Пусть z1 1 2i, |
z2 3 4i. Тогда |
|
|
|
|
|
|
|||||||||||||||||||||||
z1 z2 1 3 i 2 4 4 2i, z1 z2 1 3 i 2 4 2 6i, z1 z2 1 2i 3 4i 3 4i 6i 8i2 3 8 i 6 4 11 2i.
z |
|
1 2i |
|
1 |
2i 3 |
4i |
|
3 |
4i 6i 8i2 |
|
3 8 i 4 6 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||
z2 |
3 4i |
3 |
4i 3 |
4i |
|
32 |
42 |
25 |
|||||
|
|
|
|
|
|
||||||||
255 i 1025 15 25 i.
§2. Геометрическое изображение и тригонометрическая форма комплексного числа
Любое комплексное число z x iy можно изобразить на плоскости Oxy в виде точки M x, y с координатами x, y. В этом случае плоскость называется
комплексной, Ox – действительной осью, а Oy – мнимой осью. В некоторых случаях комплексное число z x iy представляют в виде вектора OM .
Обозначим через и r полярные координаты точки M x, y , считая нача-
ло координат полюсом, а положительную полуось Ox – полярной осью. Тогда
(см. рис. 102)
x r cos , |
y r sin . |
|
|
|
|
|
(4) |
|
Следовательно, комплексное число z можно пред- |
|
|||||||
ставить в виде x iy r cos ir sin или |
|
|
|
|
|
|
|
|
z r cos i sin . |
|
|
|
|
|
(5) |
|
|
Это и есть тригонометрическая форма комплексно- |
Рис. 102 |
|||||||
|
||||||||
го числа. Величины r |
и называются соответственно модулем и аргументом |
|||||||
комплексного числа |
z и обозначаются |
r |
|
z |
|
, |
arg z. Положительным |
|
|
|
|||||||
направлением отсчёта аргумента считается направление против хода часовой стрелки. Из соотношений (4) следует
188
5354.ru
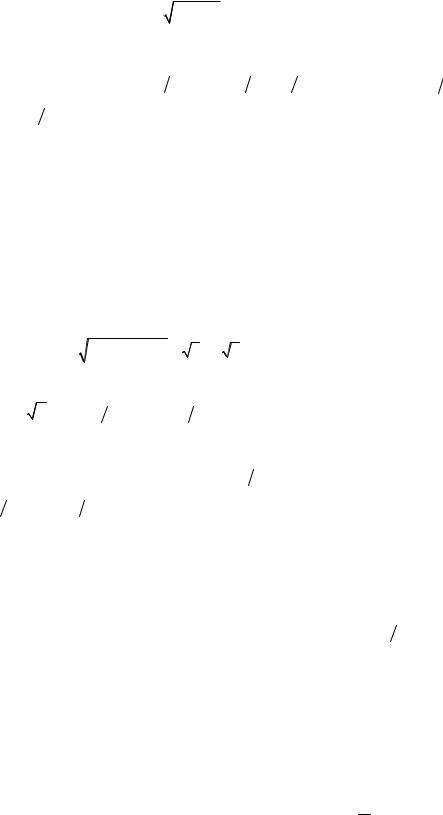
|
|
arctg |
y |
2 k, x 0, |
|
||
|
|
|
|
||||
r |
x2 y2 , |
|
x |
|
|
|
(6) |
|
|
y |
|
||||
|
|
|
|
|
2 k, x |
|
|
|
|
arctg |
|
0, |
|||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
где |
k |
– любое целое число, |
|
2 arctg |
|
y |
x |
|
|
2. |
При |
x 0 |
|
2 |
|
|
если |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k, |
||||||||||||||
|
|
|
и |
|
|
|
если y |
|
Учитывая, |
что |
|
|
и cos |
|
|
суть |
2 |
- |
|||||||||
y |
|
0, |
|
2 |
2 k, |
|
0. |
sin |
|
|
|
|
|||||||||||||||
периодические функции, при записи комплексного числа в виде (5) слагаемые 2 k опустим.
Пример. Представить числа z1 2 2i, |
z2 3i, |
z3 4 в тригонометриче- |
ской форме. |
|
|
Комплексному числу z1 на плоскости Oxy соответствует вектор OM1 с
концом в точке M1 2, 2 , |
расположенной в третьей четверти координатной |
|||||||||||||||||
плоскости (рис. 103). Использовав (6), найдем |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
r1 2 2 2 2 8 2 2, |
|
|
|
|
|
|
||||||
|
|
|
1 |
arctg[ 2 / 2 ] / 4 5 / 4. |
|
|
|
|
|
|
||||||||
Значит, |
z1 2 |
2 cos 5 4 i sin 5 |
4 . Комплексному |
|
|
|
||||||||||||
числу |
z2 |
на |
плоскости |
Oxy |
соответствует |
вектор |
|
Рис. 103 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OM2 0;3 |
, |
|
следовательно, |
|
2 2, |
|
r2 3, |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
z2 3 cos |
2 i sin |
2 . Комплексному числу |
z3 4 0i |
на плоскости Oxy со- |
|||||||||||||
ответствует |
вектор |
|
|
4;0 . |
Аргумент |
3 |
0, |
модуль |
r3 4, |
отсюда |
||||||||
OM3 |
||||||||||||||||||
|
z3 4 cos 0 i sin 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пусть |
два |
комплексных числа заданы в |
тригонометрической |
форме: |
|||||||||||||
|
z1 r1 cos 1 |
i sin 1 , |
z2 r2 cos 2 |
i sin 2 . Найдём |
z1 z2 |
и |
z1 z2 , |
учитывая, что |
||||||||||
i2 1. Получим
z1 z2 r1 cos 1 i sin 1 r2 cos 2 i sin 2
r1r2 cos 1 cos 2 i2 sin 1 sin 2 i sin 1 cos 2 i cos 1 sin 2
или
z1 z2 r1r2 cos 1 2 i sin 1 2 . |
(7) |
Вычислим z1 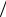 z2 , умножив числитель и знаменатель на z2 , при этом учтём (3):
z2 , умножив числитель и знаменатель на z2 , при этом учтём (3):
189
5354.ru
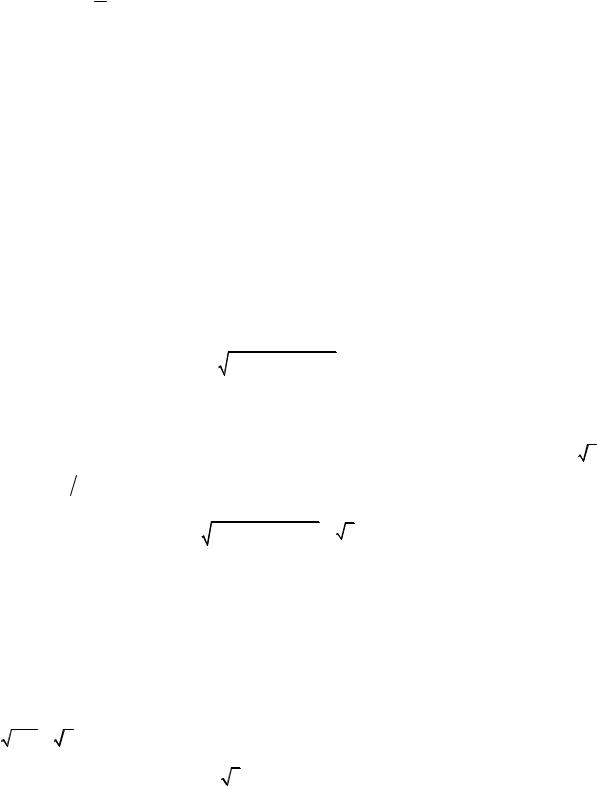
z1 |
|
z1 |
|
|
|
|
|
|
r1 cos 1 i sin 1 r2 cos 2 i sin 2 |
|
|||
|
z2 |
|
|||||||||||
z |
|
|
z |
|
|
|
|
|
|
|
r 2 |
|
|
2 |
|
2 |
z |
2 |
|
|
|||||||
|
|
|
|
|
|
2 |
|
||||||
r1 cos 1 cos 2 i2 sin 1 sin 2 i sin 1 cos 2 cos 1 sin 2 r2
или z1 / z2 (r1 / r2 )[cos 1 2 i sin 1 2 ].
§ 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа
Возведение в степень. Пусть |
z r cos i sin . Возведём z |
в степень n, |
|||||||
где n – целое положительное число. Это означает, что число |
z |
надо умно- |
|||||||
жить |
само |
на |
себя |
n |
раз. |
Используя |
(7), |
получим |
|
zn r cos i sin n rn cos n i sin n . |
Это соотношение |
называется форму- |
|||||||
лой Муавра.
Извлечение корня. Корнем n -й степени из комплексного числа называется такое комплексное число, n -я степень которого равняется подкоренному чис-
лу, т. е. n r cos i sin cos i sin , если
r cos i sin n cos n i sin n . У равных комплексных чисел модули долж-
ны быть равны, а аргументы могут лишь отличаться на число, |
кратное 2 . |
||||||||||||||
Отсюда |
n |
r, |
n |
2 k, |
где |
k |
– любое целое число, следовательно, |
n |
r , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 k |
|
n. Итак, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 k |
|
2 k |
|
|
||
|
|
|
|
|
|
n r cos i sin n r cos |
|
i sin |
|
|
. |
(8) |
|||
|
|
|
|
|
|
n |
|
n |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Придавая k |
значения от 0 до n 1, получим n различных значений корня. Для |
||||||||||||||
всех других |
|
k |
соответствующие значения корня будут совпадать с найден- |
||||||||||||
ными. Таким образом, корень n -й степени из комплексного числа имеет n значений.
Пример. Решить уравнение z3 1 i.
Представим число 1 i в тригонометрической форме, для этого найдём
r 1 1 2, arctg1 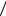 4. Отсюда
4. Отсюда
1 i 2 cos 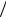 4 i sin
4 i sin 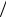 4 .
4 .
Найдем корни уравнения по формуле (8):
190
5354.ru
