Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SalimovRB_matematika_gl_1-20_2011_web

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

3.88 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 4021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

A0 , A1, , An

Первый интеграл правой части (18) равен

Jk 1. Второй интеграл в (18)

проинтегрируем по частям,

полагая

U t,

1 d (t2 m2 ) . При

(t2 m2 )k

2 (t2 m2 )k

этом

(1/ 2) t

d t

m2 k 1

(

k 1)

Поэтому

m2 k 1

k 1

dt,

k 1

2( k 1)

интеграл в правой части равен Jk 1.

Окончательно выражение (18) примет вид

2k 3

Jk 1. (19)

1 t

k 1

Эта формула называется рекуррентной. Заменив в (19) k на k 1, выразим Jk 1 через Jk 2 . Заменив k на k 2 , выразим Jk 2 через Jk 3 и т. д. Наконец, выразим J2 через J1. Но J1 вычисляется по формуле (15), следовательно, найдём J2 , затем J3 , , Jk . Подставив Jk в (17), найдём Mk , учитывая, что t x p2.

§ 6. Разложение многочлена на множители

Функция вида

f x A0 xn A1xn 1 An 1x An

(20)

называется многочленом или полиномом степени n, n – целое положительное число. Числа являются коэффициентами многочлена, их будем считать действительными числами. Число x a, при котором многочлен обращается в нуль ( f a 0) , называется корнем многочлена.

Нетрудно проверить, что если комплексное число i ( , – действительные числа) является корнем многочлена с действительными коэффициентами, то сопряжённое число i также будет корнем этого многочлена. Так что в случае многочлена с действительными коэффициентами комплексные корни являются парными (комплексно сопряжёнными). Согласно основной теореме алгебры всякий многочлен степени n имеет n корней, которые могут быть действительными или комплексными. Отсюда следует, что любой мно-

201

5354.ru

m n,

гочлен степени n вида (20) может быть разложен на произведение линейных двучленов и квадратных трёхчленов

fx A0 x a x b s x2 mx n x2 px q (21)

Вэтой формуле все величины в правой части кроме x есть действительные числа, s, , ... – целые положительные числа. Представленные в (21) квадрат-

ные трёхчлены не разлагаются на линейные множители. Это означает, что указанные квадратные трёхчлены имеют комплексные корни. Считается, что квадратные трёхчлены, которые можно разложить на линейные двучлены, уже разложены. Кроме того, предполагается, что в правой части (21) нет одинаковых множителей, т. е. предполагается, что все одинаковые множители уже объединены в степени. Множителю x a отвечает простой действи-

тельный корень x a многочлена (21). Множителю x b s – кратный корень x b кратности s многочлена. Множителю x2 mx n отвечает простая пара комплексно сопряжённых корней многочлена, а множителю x2 px q – па-

ра комплексно сопряжённых корней кратности .	В дальнейшем будем счи-
тать, что корни многочлена f x , следовательно,	и представление (21) из-
вестны.

§ 7. Разложение правильной рациональной дроби на простейшие дроби

Рациональной называется функция, представляющая собой отношение двух многочленов

Q x	B0 xm B1xm 1 Bm 1x Bm		.	(22)
f x	A0 xn A1xn 1	An 1x An

Если m n, то дробь (22) называется правильной рациональной дробью.

Если то дробь (22) называется неправильной дробью.

Всякую неправильную рациональную дробь путём деления числителя на знаменатель по правилу деления многочленов можно представить в виде

суммы	некоторого многочлена	и правильной рациональной	дроби, т. е.
Q x / f	x M x F x / f x , где	M x – многочлен, F x / f x	– правильная

рациональная дробь.

202

5354.ru

x2 mx n .

Разложим знаменатель f x на множители по формуле (21), в которой всюду в дальнейшем будем считать, что A0 1, получим

f x x a x b s x2 mx n x2 px q		(23)
Заметим, что если A0 1 , то заданную дробь F x	f x нужно преобразовать,
поделив и числитель, и знаменатель на A0 .

Без доказательства запишем следующее утверждение.

Если знаменатель дроби представлен по формуле (23), то правильную

дробь F x

f x

можно разложить на сумму простейших дробей:

F x

Mx N

...

f x

x a

x b

x b 2

x b s

mx n

P x Q

(24)

...

x2 px

2 px q 2 ... x2 px q

ЗдесьA, B1,

B2 ,

–

неопределённые постоянные, их нужно найти. Из (24)

видно, что простому корню x a знаменателя в этой формуле отвечает одна дробь, а простой паре комплексно сопряжённых корней знаменателя (корней множителя x2 mx n ) – тоже одна дробь Mx N Корням крат-

ности s или знаменателя в разложении (24) отвечает сумма соответственно s и простейших дробей. Выражение в правой части (24) приведём к общему знаменателю (ясно, что он равен f x ), тогда будем иметь

F x / f x x / f x .

(25)

Очевидно, что x представляет собой многочлен, который получается по-

сле объединения членов, содержащих одинаковые степени x, при приведении к общему знаменателю правой части (24). Из (25) следует

F x x .

(26)

Здесь F x – заданный многочлен, x	– многочлен, коэффициенты	которо-
го содержат искомые коэффициенты.	Соотношение (24) является	тожде-

ственным, т. е. выполняется при всех x. Соотношение (25), а потому и (26) являются также тождественными и выполняются при всех x. Так как соотно-

шение (26) выполняется для всех	x , то коэффициенты многочленов
F(x), (x) при одинаковых степенях x	равны, в чем легко убедиться, подста-

вив значение x 0 в (26) и в соотношения, получаемые из последнего после-

203

5354.ru

довательным дифференцированием по x . Приравняв коэффициенты при одинаковых степенях x в правой и левой частях (26), получим систему уравнений, содержащих искомые коэффициенты A, B1, B2 , ... Этих уравнений будет столько же, сколько имеется неизвестных коэффициентов. Из этой системы и найдём все коэффициенты A, B1, B2 , ...

Приведенные рассуждения можно рассматривать как нестрогое обоснование (24). Уравнения для нахождения вышеуказанных искомых коэффициентов можно получить иначе, а именно, подставив в (26) вместо x любые числа. При каждой подстановке будем иметь определённое уравнение. В итоге получим число уравнений, равное числу неизвестных коэффициентов. На практике обычно два вышеуказанных подхода комбинируют. Отметим, что в (26) вместо x выгодно подставлять не любые значения, а значения, равные действительным корням f x .

Пример 1.

x 3

(27)

x3 x

x x 1 x 1

x 1

x 3

x 1

x3 x

x x 1 x 1

x 3 A				Bx			Cx			(28)
x 3 A		x 1	x 1	Bx		x 1	Cx		x 1

x 3 x2 A B C x B C A.

Приравняем коэффициенты при одинаковых степенях x слева и справа и получим систему уравнений

	0 A B C;		1 B C;		3 A.
Отсюда найдём A, B, C. Но проще эти коэффициенты найти из других уравне-
ний, которые получим, подставив в (28)				вместо x значения, равные корням
знаменателя: x 0,	x 1,	x 1.	При	этом	будем иметь соответственно

3 A,	4 2B,	2 2C.Следовательно,				A 3,		B 2,	C 1. Таким обра-
зом, (27) примет вид
			x 3	3	2		1	.
				3	x 1		x 1	.
			x3 x x		x 1		x 1

204

5354.ru

Пример 2.

x 5

x3 3x2

x 1 x 2 2

x 2 2

Правую часть приведём к общему знаменателю, затем, отбросив общий знаменатель, получим

x 5 A x 2 2

x 1 x 2 B2 x 1 .

(29)

В (29) положим x 1,

затем x 2,

тогда

6 9A,

A 2 / 3,

B2 1.

3 3B,

Чтобы получить уравнение для B , сравним коэффициент при x2

слева и

справа в (29):

0 A B1.

Отсюда

найдем

B1 A 2 / 3.

Окончательно будем

иметь

x 5

x3 3x2 4

3 x 1

3 x 2

x 2 2

Пример 3.

Cx D

1 x

x3 x 1

x 1

x2 x 1

Выражение в правой части приведём к общему знаменателю, затем отбросим знаменатель. Тогда получим

12 A x 1

x2 x

B x

Cx D

(30)

x 1

Положим x

затем

x 1.

Будем иметь при этом соответственно

12 2 A,

A 6,

B 2.

6B,

Ещё два уравнения для нахождения C и D получим, сравнив в (30) слева и

справа коэффициенты при x3

и свободные члены:

0 A B C, 12 A B D C A B C 4.

Далее находим D 12 A B 4. Таким образом,

4x 4

(31)

x4 x3 x 1

x 1

x2 x 1

205

5354.ru

§ 8. Интегрирование рациональных дробей

Дана рациональная дробь Q x f x , нужно найти от нее интеграл[Q x / f x ]dx. Здесь нужно различать два случая:

Дробь Q x f x является правильной. Тогда разложим её на сумму

простейших дробей, и искомый интеграл будет равен сумме интегралов от простейших дробей.

Дробь Q x f x является неправильной. Тогда запишем её в виде сум-

мы Q x

f x M x F x

f x ,

где M x

– многочлен, а F x

f x – пра-

вильная рациональная дробь. Последнюю разложим на сумму простейших дробей. После этого проинтегрируем.

Итак, интеграл от рациональной дроби всегда может быть вычислен.

Пример. Вычислить J 12 dx. x4 x3 x 1

Воспользуемся формулой (31). Тогда

Интеграл	4	x 1
			dx
		x2 x 1

6 2 4x 4

J x 1 dx x 1 dx x2 x 1 dx

6ln | x 1| 2ln | x 1| 4 x2 x x1 1 dx.

предлагается вычислить самим, использовав материал

§ 5 настоящей главы.

§ 9. Интегрирование простейших иррациональных функций

Рациональная функция представляет собой отношение двух многочленов, следовательно, она определяется формулой, содержащей конечное число четырёх арифметических действий: сложение, вычитание, умножение и деление, выполненных над независимой переменной, постоянными и получаемыми при этом выражениями.

Иррациональной называется функция, которая определяется формулой, содержащей конечное число четырех арифметических действий и извлечение корня с целым показателем, выполненных над независимой переменной, постоянными и выражениями, представляющими рациональные функции от независимой переменной.

Рассмотрим интеграл

206

5354.ru

		ax b		ax b
J	R x, m		, p		, ... dx.

		a1x b1		a1x b1

R – рациональная функция своих аргументов, m, p, ... , a, b, a1, b1 – заданные

действительные числа, причем показатели корней – целые числа. Под всеми корнями стоит одно и то же выражение, в котором и числитель, и знаменатель дробей подкоренного выражения содержат x в первой степени. Пусть n – наименьшее общее кратное показателей корней m, p, ..., т. е. число, которое делится без остатка на эти показатели. Чтобы избавиться от иррациональности, сделаем замену

ax b U n , a1x b1

Следовательно,

dx x'

ab1 ba1

nU n 1dU.

(a a U n )2

ab1 ba1

b1U

,U n / m ,U n / p ,

nU n 1dU.

a a1U n

a a1U

x bU n b .

a a1U n

Тогда интеграл

Но числа nm , n

(32)

J примет вид

p, ... суть целые

числа, так как по условию n – наименьшее кратное чисел m, p, ... Под знаком интеграла мы получим рациональную функцию, которая может быть проин-

тегрирована. В частности, если a1 0,						b1 1,			то подкоренное выражение и за-
мена (32) примут вид ax b и ax b U n						соответственно.
Пример. Вычислить интеграл					x		dx.
					x 4

Сделаем замену x 4 U 2. Тогда x U 2 4,										dx 2UdU и
	x		U 2 4					2		U 3
		dx	U	2UdU 2 U						4 dU 2 3	4U C,
	x 4
здесь согласно замене U			x 4.
§ 10. Интегрирование тригонометрических функций
Рассмотрим интеграл J1 R sin x, cos x dx,										где R – рациональная функция
своих аргументов. Покажем, что J1					приводится к интегралу от рациональной
функции и может быть вычислен. Сделаем замену
									tg(x 2) U.		(33)

При этом x / 2 arc tgU , следовательно, x 2 arctgU , поэтому

207

5354.ru

dx 2 / 1 U		dU.	(34)
	2

Чтобы представить подынтегральную функцию через U , нужно sin x и cos x выразить через U , т. е. через tg(x2). Известно, что sin x 2sin x2 cos x2 . Эту формулу запишем так:

sin x 2sin x2 cos x2 /[sin2 x2 cos2 x2 ].

Числитель и знаменатель дроби в правой части разделим на cos2 x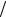2 и получим sin x [2 tg x2 ]/[1 tg2 x2 ]. В силу (33) будем иметь

sin x 2U /(1 U 2 ).			(35)
Аналогично поступим с cos x : cos x cos2 x	2 sin2 x	2 ,
cos x [cos2 x 2 sin2 x 2 ] /[cos2	x 2 sin2	x 2 ].

И числитель, и знаменатель правой части последней формулы поделим на cos2 x2 , тогда cos x [1 tg2 x2 ]/[1 tg2 x2 ], поэтому

cos x (1 U 2 ) /(1 U 2 ).

(36)

Выражения (34) – (36) подставим в интеграл J1 , который теперь примет вид

2dU

1 U 2

. Здесь подинтегральная функция является уже ра-

1 U

циональной функцией от U. Вычислив J1 , подставим в полученное выраже-

ние U tg(x 2)

и вернёмся к исходной переменной.

Пример. Вычислить интеграл dx sin x.

Сделаем замену (33). Тогда sin x

и dx будут выражаться формулами (34),

(35), поэтому

2 (1 U 2 )

U ln |U | c ln | tg(x 2) | C.

sin x

2U (1 U 2 )

Замена (33) при вычислении интегралов вида J1 всегда приводит к успе-

ху, т. е. позволяет вычислить этот интеграл до конца. В связи с этим замену (33) называют универсальной. В силу своей общности она не всегда является выгодной, поэтому иногда лучше применять не (33), а другую замену. Отметим три таких случая.

208

5354.ru

R sin x cos xdx.

Здесь

лучше

сделать

замену U sin x, тогда

dU sin x x dx cos xdx и интеграл примет вид R U dU.

R cos x sin xdx. Здесь надо взять U cos x,

тогда исходный интеграл при-

мет вид R U dU .

R cos2 x, sin2

x dx,

здесь sin x

и cos x

входят только в чётных степенях.

Сделаем замену tg x U ,

тогда

x arctgU , dx

cos2

, sin2

x tg2 x cos2 x.

U 2

tg2 x

Следовательно,

cos2 x 1/(1 U 2 )

и sin2 x U 2

/(1 U 2 ). Поэтому рассматриваемый

интеграл запишется так:

dU.

1 U

cossin

xx sin xdx.

Пример 1. Вычислить интеграл cossin 4

xx dx

Пусть U cos x,

тогда dU sin xdx и последний интеграл примет вид

1 U4

( 1)dU dU2

dU4

cos x

3cos

Пример 2. Вычислить интеграл

sin2

dx.

cos

Положим U tg x, тогда x arctgU,

dx (1 U 2 ) 1 dU и

sin2

U 2 (1 U 2 )2

dU U

/ 3 C (1/ 3) tg

x C.

cos

(1 U

)

(1 U

)

§11. Интегрирование иррациональных функций

спомощью тригонометрических замен

Рассмотрим интеграл J2 R x, ax2 bx c dx. Здесь	подинтегральная
функция R – рациональная функция своих аргументов, a, b, c	– заданные дей-

ствительные числа, a 0 . Преобразуем подкоренное выражение. Вынесем за

скобки	a, а затем полученное выражение дополним до полного квадрата
суммы:	ax2 bx c	a x b /(2a) 2 c b2 /(4a).	Введём обозначения a m2 ,
		209	5354.ru
			5354.ru

c b2 /(4a) n2 . Здесь знаки правых частей мы должны считать совпадающими со знаком левой части в каждом выражении, например, если a 0, то берём a m2 , если a 0, то a m2 . Кроме того, в рассматриваемом интеграле

сделаем замену x b /(2a) t. Отсюда	x t b /(2a),			значит,				dx xt dt dt. Теперь

исходный интеграл принимает вид			b	2		2			2		Здесь, пере-
	J2	R t		, m	t		n			dt.
	J2	R t	2a	, m	t		n			dt.
			2a

брав знаки перед слагаемыми под корнем, получим четыре различных случая, так как каждый из знаков первого слагаемого сочетается с каждым из знаков второго слагаемого. Однако один из случаев, когда под знаком корня стоитm2t2 n2 , мы должны отбросить, так как получаем отрицательное подкоренное выражение и, соответственно, мнимую величину. Таким образом, остаётся рассмотреть лишь три следующих варианта:

R t

dt;

R t

, m

dt;

		b		2	2		2
J2	R t		, n		m	t		dt.
J2	R t	2a	, n		m	t		dt.
		2a

Чтобы избавиться от корня, необходимо сделать следующие замены соответ-

ственно: t

tgU; t

; t

sinU.

m cosU

Пример. Вычислить

n2 x2 3 dx.

Сделаем

замену

x nsinU,

при этом

dx xU dU n cosUdU,

отсюда

n cosUdU

n3 cos3 U

tgU C.

Здесь

согласно

замене

n2 x2 3

cos2 U

U arcsin (x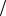n).

Замечание. В дальнейшем мы докажем, что для любой непрерывной функции f (x) существует первообразная F(x) , т. е. неопределенный интеграл

f (x)dx F(x) C

(см. §4 главы 12). Но, оказывается, не всегда этот неопределенный интеграл представляет собой элементарную функцию, т. е. не всегда он может быть представлен одной формулой, выраженной через конечное число основных элементарных функций. К таким интегралам относятся

e x2 dx,	dx	,	sinx xdx,	cosx xdx и т. д.
	ln x
			210

5354.ru

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 4021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.04.2019125.44 Кб1RTsB_test.doc
#
12.05.2015371.27 Кб10rulturologiy 2.pdf
#
14.11.2018293.89 Кб4russkij-yaz.-egye-chast-s-yenciklopediya.doc
#
17.03.2016150.23 Кб9rutrvar56.pdf
#
17.03.2016311.15 Кб4ryady_metod_ukazaniya_kgasu_5354.pdf
#
12.05.20153.88 Mб42SalimovRB_matematika_gl_1-20_2011_web.pdf
#
12.05.20153.69 Mб71SalimovRB_matematika_gl_1-9_2011_web.pdf
#
11.05.2015988.67 Кб44Sbornik_testov_s_otvetami_marketing.doc
#
12.05.20159.79 Mб13SGH_i900_service_manual-spaces_ru.pdf
#
12.05.2015526.35 Кб48Shavali_Burova_109_13.pdf
#
11.05.2015710.66 Кб23Shpargalka_po_pravookhranitelnym_organam.doc