
SalimovRB_matematika_gl_1-20_2011_web
.pdfравны нулю. Без доказательства отметим, что при m n данное определение ранга матрицы равносильно другому, используемому здесь определению: рангом матрицы называется число ненулевых строк в эквивалентной треугольной или ступенчатой матрице. Ясно, что для определения ранга матрицы сначала её нужно преобразовать методом Гаусса и привести к треугольной или ступенчатой матрице, эквивалентной исходной.
Пусть система уравнений (20) преобразована методом Гаусса и приведена либо к системе (21), либо к системе (22). При этих преобразованиях происходят соответствующие преобразования основной и расширенной матриц системы (20). Совместность системы (20) равносильна отсутствию в преобразо-
ванной |
системе |
(21) или (22) противоречивого соотношения |
0x1 0x2 |
0xn b, |
b 0 (здесь равные нулю коэффициенты образовали бы |
нулевую строку основной матрицы преобразованной системы, а эти же коэффициенты и число b 0 - ненулевую строку расширенной матрицы этой системы). Это в свою очередь равносильно совпадению числа ненулевых строк основной и расширенной матриц преобразованной системы (21) или (22). А это последнее, в свою очередь, равносильно совпадению рангов основной и расширенной матриц исходной системы. Итак, справедлива
Теорема Кронекера – Капелли. Если система уравнений совместна, то ранги её основной и расширенной матриц равны, и наоборот, если ранги основной и расширенной матриц равны, то система совместна.
§ 8. Однородные системы
Система уравнений (20) называется однородной, если все ее свободные члены равны нулю: b1 0, b2 0, , bm 0 . Ясно, что однородная система всегда
совместна, так как имеет очевидное |
тривиальное нулевое решение |
x1 0, x2 0, , xn 0 . Если среди чисел x1, |
x2 , , xn имеется хотя бы одно, от- |
личное от нуля, то такое решение системы называется ненулевым.
Пусть в однородной системе (20) число уравнений меньше числа неизвестных ( m n ). Такая система методом Гаусса приведётся к ступенчатой системе, так как к треугольной системе мы можем прийти, лишь когда m n . Но ступенчатая система имеет бесконечное множество решений, среди которых обязательно найдётся ненулевое. Например, в системе (21) ненулевое решение получим, взяв xr 1 0 . Таким образом, справедлива
71
5354.ru
Теорема 1. Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевые решения.
Рассмотрим случай, когда в однородной системе (20) m n . Для такой системы может быть доказана
Теорема 2. Если однородная система из n уравнений с n неизвестными имеет ненулевые решения, то её определитель равен нулю, и наоборот, если определитель указанной однородной системы равен нулю, то эта система имеет ненулевые решения.
Доказательство. Докажем сначала первую часть теоремы: дана однородная система (20), в которой m n и b1 0, b2 0, , bn 0 , и она имеет ненуле-
вые решения; нужно доказать, что её определитель равен нулю. Предположим противное, т. е. что её определитель 0 . Тогда решение
этой системы из n |
уравнений с n |
неизвестными можем записать по форму- |
|
лам Крамера x1 1 |
/ , x2 2 |
/ , , |
xn n / . Это будет единственное реше- |
ние. Но все определители 1, |
2 , , n содержат столбец свободных членов, |
||
состоящий из одних нулей, поэтому все они равны нулю. Следовательно, по формулам Крамера получим единственное решение рассматриваемой однородной системы x1 0, x2 0, , xn 0 – нулевое решение. Это противоречит
условию теоремы, согласно которому система имеет ненулевое решение, следовательно, предположение, что 0 , должно быть отброшено.
Докажем вторую часть теоремы: определитель однородной системы (20) n уравнений с n неизвестными равен нулю; нужно доказать, что система имеет ненулевые решения.
Заданную однородную систему преобразуем методом Гаусса, при этом придём к ступенчатой системе. Если бы пришли к треугольной системе, то, как было показано раньше, пришли бы к заключению, что определитель исходной системы не равен нулю, что не согласуется с условием теоремы. Итак, система обязательно приводится к ступенчатой. Последняя имеет бесконечное множество решений, среди которых найдутся и ненулевые, поэтому исходная система имеет ненулевые решения. Теорема доказана.
При решении однородной системы целесообразно преобразовать её методом Гаусса и привести к ступенчатой или треугольной системе.
72
5354.ru
ГЛАВА 4. ТЕОРИЯ ПРЕДЕЛОВ
§1. Обозначения, переменные, интервалы
Вматематике используется большое количество символов, рассмотрим некоторые из них.
Квантор общности – символ . Запись x читается так: «для любого x …», «для всех x …». Например, запись x 0 означает «для любого положительного x ».
Квантор существования – это символ . Запись x читается так: «суще-
ствует такое x , что …». Запись x 0 означает «существует такое положительное x , что …».
Символ обозначает логическое следствие. Запись |
A B означает, что |
|||
из утверждения A следует утверждение B . Символ обозначает логическую |
||||
равносильность. Запись |
|
означает, что из утверждения |
A следует |
|
утверждение B , и наоборот. |
|
|
|
|
Например, пусть A |
есть |
утверждение «Треугольник со |
сторонами |
|
a, b, c c a, c b является прямоугольным треугольником», а B есть утвер-
ждение « c2 a2 b2 ». Видим, что , так как и, наоборот, . Например, запись
0 N x N | f (x) b |
читается так: для любого положительного числа существует такое число N , что для всех x N имеет место неравенство | f (x) b | .
Переменные величины. Интервалы. В математике рассматривают только численные значения величин, при этом отвлекаются от их конкретного физического содержания.
Постоянной называется величина, которая принимает лишь одно численное значение. Постоянные величины обозначают обычно буквами a, b, c и
т. д.
Переменной называется величина, которая принимает различные численные значения. Численные значения переменной образуют некоторое множество действительных чисел. Например, множество чисел, удовлетворяющих неравенству a x b . Это множество называется (открытым) интервалом и обозначается или a, b называются концами интервала.
73
5354.ru
Множество чисел, удовлетворяющих неравенству a x b , называется за-
крытым или замкнутым интервалом и обозначается a,b .
Рассматриваются также полузакрытые (полуоткрытые) интервалы a x b , a x b , обозначаемые соответственно [a,b) , (a,b] или [a,b[ , ]a,b].
Интервалы могут быть бесконечными. Множество чисел, удовлетворяющих неравенству x a , называется бесконечным интервалом и обозначается
a, или ]a, [ . |
Множество всех чисел, удовлетворяющих |
неравенству |
|||||
x a |
, обозначается |
[a, |
|
) или [a, |
|
|
|
|
|
[ . Множество всех чисел, удовлетворяю- |
|||||
щих неравенству x b , обозначается ( ,b) |
или ] ,b[ . Множество всех чи- |
||||||
сел, удовлетворяющих неравенству x b , |
обозначается ( ,b] |
или ] ,b] . |
|||||
Наконец, множество всех действительных чисел есть бесконечный интервал, который обозначается или ] , [ .
§ 2. Свойства абсолютной величины числа
Абсолютной величиной числа x называется число |
|
x |
|
, равное |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x при |
x 0, |
(1) |
||||||||||||||||||||
| x | |
|
при |
|
|
x 0. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||
Из этого определения вытекает, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
|
|
|
|
|
x |
|
|
, |
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
|
0, x 0. |
|
|
|
(3) |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
Кроме того |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
|
x |
|
. |
|
|
|
|
|
|
|
|
|
(4). |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Действительно, при x 0 по формуле (1) имеем |
x |
|
x |
|
, и неравенство (4) |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
выполняется. При x 0 согласно (1) имеем x |
|
x |
|
|
|
x |
|
, так как |
|
x |
|
0 , т. е. сно- |
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
ва выполняется (4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Покажем, что соотношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
| x | ( 0) |
|
|
|
(5) |
|||||||||||||||||||||||||||||
равносильно неравенствам |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x . |
|
|
|
(6) |
||||||||||||||||||||||||||||
Действительно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
74
5354.ru

| x | |
x |
при |
x 0, |
0 x , |
x . |
||
|
x |
при |
x 0 |
|
x 0 |
||
|
|
|
|
||||
Свойства абсолютной величины:
x1 x2 |
|
|
|
x1 |
|
|
|
x2 |
|
, |
|
x1 x2 |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x1 x2 |
|
|
|
x1 |
|
|
|
x2 |
|
, . |
|
|
|
x1 / x2 |
|
|
|
x1 |
|
/ |
|
x2 |
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Эти свойства легко обосновать с помощью (1) – (4).
§ 3. Функция, способы задания
Пусть x – переменная величина, M – множество ее значений, y – другая переменная величина и N – множество её значений.
Функцией называется правило, по которому каждому значению x из множества M ставится в соответствие определённое значение y из множества N при условии, что каждое значение y из множества N отвечает хотя бы одно-
му x из M . Переменная x называется независимой переменной или аргумен-
том, а зависимая переменная y – функцией. Множество M называется обла-
стью определения функции, а N – областью значений функции. Введённая функция обозначается y f (x) (здесь f означает не переменную, а вышеуказанное правило, устанавливающее соответствие между x и y ). Говорят, что функция y f (x) отображает множество M на множество N . Вместо f при-
меняются и другие буквы, например, y F(x) , y (x), y y(x) |
и т. д. В част- |
|||
ности, если для функции y f (x) |
конкретному значению x x0 |
отвечает кон- |
||
кретное значение y y0 , то пишут |
y0 f x0 или y |
|
x x0 y0 . |
|
|
|
|||
|
|
|||
Табличный способ задания функции. Задают ряд значений аргумента x
и указывают соответствующие им значения функции y . Примерами такого способа задания функции являются известные таблицы логарифмов и тригонометрических функций.
Графический способ задания функции – это способ задания функции y f (x) с помощью её графика.
Графиком функции y f (x) называется множество точек на плоскости Oxy, для каждой из которых абсцисса x равна значению аргумента, а ордината равна соответствующему значению функции y f (x) .
75
5354.ru
Как правило, будем рассматривать функции, графики которых представляют собой сплошные линии или линии, состоящие из нескольких сплошных кривых. Ясно, что соотношение y f (x) является уравнением этой линии.
Аналитический способ задания функции. Здесь функция задаётся фор-
мулой, например, y x2. Однако функция может задаваться одновременно несколькими формулами для различных интервалов изменения x. Например,
x |
|
при |
x 0, |
y |
2 |
при |
x 0. |
x |
Но если функция задана одной формулой, без дополнительного указания области определения, то под последней понимается совокупность всех значений x, для которых эта формула имеет смысл и по которым можно вычислить соответствующие значения функции. Например, для функции y 1/(x 2) областью определения является множество всех x, отличных от 2, т. е. множество x 2 и x 2 или совокупность интервалов ( ,2) и (2, ) . При x 2 имеем x 2 0 , и формула теряет смысл.
Основные элементарные функции:
постоянная функция y C const ;
степенная функция y xn , n – любое действительное число;
|
показательная функция y ax |
|
|
|
|
|
|
|
|
|
|
a |
0, |
a |
1 ; |
|
|
|
|||
|
логарифмическая функция y loga x |
a 0, a 1 ; |
|
|
||||||
|
тригонометрические функции y sin x, |
y cos x, |
y tg x, |
y ctg x ; |
||||||
|
обратные |
тригонометрические |
функции |
y arcsin x, |
y arccos x, |
|||||
y = arctg x , y arcctg x. |
|
|
|
|
|
|
|
|
||
Определение сложной функции. Дана функция |
y f (U ) , |
причём аргу- |
||||||||
мент U |
является функцией от x , т. е. |
|
U (x) |
и область значений функции |
||||||
U (x) |
является частью области определения функции |
y f (U ) . Следова- |
||||||||
тельно, |
каждому x |
из области определения (x) отвечает определённое зна- |
||||||||
чение U (x) , а этому значению U отвечает определённое значение y f (U ) . Таким образом, каждому указанному x отвечает определённое значение y . Это означает, что y есть функция от x . Она называется сложной функцией от x и записывается в виде y f (x) , где – внутренняя функция, f –
76
5354.ru

внешняя |
функция, U (x) – промежуточный аргумент. Например, пусть |
y sinU, |
где U lg x , тогда получим сложную функцию y sin lg x . |
Ясно, что, рассуждая аналогично, можно ввести сложную функцию, состоящую из трёх и большего числа функций.
Элементарной называется функция, определяемая одной формулой, составленной из основных элементарных функций, с помощью конечного числа четырёх арифметических действий , , /, и с помощью конечного числа
операций взятия функции от функции.
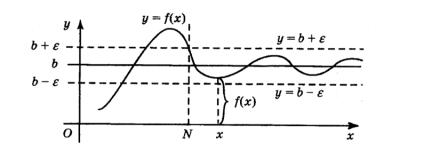
§ 4. Предел функции при x и его геометрический смысл
Пусть x – переменная величина, которая принимает положительные значения и неограниченно увеличивается. В этом случае будем говорить, что x
стремится к плюс бесконечности и писать x . Пусть при этом заданная функция y f (x) принимает значения, всё более и более близкие к некоторому числу b , в том смысле, что величина f (x) b уменьшается и приближает-
ся к нулю. В этом случае будем говорить, что число b есть предел функции y f (x) при x .
Определение. Число b называется пределом функции y f (x) при x ,
если для любого положительного числа , каким бы малым оно ни было, найдётся такое положительное число N , что для всех x N выполняется неравенство | f (x) b | , т. е. символически 0 N x N | f (x) b | . В
этом случае будем писать lim f (x) b.
x
Подчеркнём, что – любое положительное число, сколь угодно малое. Другими словами, если число b есть предел функции f (x) приx , то для всех сколь угодно больших x значения функции f (x) сколь угодно мало отличаются от b . Ясно, что число N зависит от выбора числа : чем меньше ,
тем больше N . Иначе говоря, N N( ), |
т. е. N есть функция от . |
|||||||
|
Покажем, что функция f (x) 5 1/ x |
имеет предел при x , равный 5. В |
||||||
самом деле, |
f (x) 5 1/ x . Так как x |
– |
величина положительная, то условие |
|||||
| f (x) 5| |
примет вид 1/ x |
или |
x . |
Таким образом, для всех x |
||||
имеем | f (x) 5 | , каким бы малым число |
|
ни было. |
Это означает, что |
|||||
функция f x 5 1/ x имеет предел, |
равный 5, |
при x . |
В качестве числа |
|||||
N , |
фигурирующего в определении предела, можем взять N 1/ . Отсюда вид- |
|||||||
но, |
что с |
уменьшением |
число |
N увеличивается. |
В этом примере |
|||
77
5354.ru
f (x) 5 1/ x 5 всегда, так как x 0 . Поэтому функция стремится к пределу 5, оставаясь больше своего предела, когда x . Аналогично можно показать,
что функция 2 1/ x |
имеет предел, |
равный 2, и при x эта функция |
2 1/ x 2 для всех x, |
так как x 0 . |
Таким образом, функция стремится к 2, |
оставаясь при этом меньше своего предела. Нетрудно проверить, что функция 1 (sin x) / x при x имеет предел, равный 1. Здесь x – угол, измеряемый в радианах. Ясно, что эта функция при x может принимать значения как большие, так и меньшие 1 в зависимости от знака sin x. Эта функция стремится к своему пределу, принимая значения и меньшие, и большие, и равные
этому пределу. |
Но функция |
f (x) |
при |
x может и не иметь предела. |
||||||||||||||||||
Например, |
пусть |
f (x) sin x. |
Если x , то sin x изменяется, |
принимая лю- |
||||||||||||||||||
бые значения в интервале [ 1,1], и ни к какому пределу не стремится. |
|
|||||||||||||||||||||
Выясним геометрический смысл предела lim f (x) b. Неравенство |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| f (x) b | |
|
|
|
(1) |
|
равносильно неравенствам f (x) b |
или |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b f (x) b . . |
|
|
|
(2) |
|
Если |
lim |
|
f (x) b |
и для любого числа 0 найдётся такое число |
|
N , |
что для |
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
всех x N имеет место (1), сле- |
|
|
|
|
|
|
|
|
||||||||||||||
довательно, и (2), то геометри- |
|
|
|
|
|
|
|
|
||||||||||||||
чески это означает, что для всех |
|
|
|
|
|
|
|
|
||||||||||||||
точек графика |
y f (x) , |
абсцис- |
|
|
|
|
|
|
|
|
||||||||||||
сы x |
которых |
удовлетворяют |
|
|
|
|
|
|
|
|
||||||||||||
неравенству |
x N , |
|
ординаты |
|
|
|
|
|
|
|
|
|||||||||||
f (x) лежат в интервале (2). Это |
|
|
|
|
|
|
|
|
||||||||||||||
означает, что указанные точки, |
|
|
|
Рис. 40 |
|
|
|
|
||||||||||||||
образующие |
соответствующий |
|
|
|
|
|
|
|
|
|||||||||||||
участок графика, |
лежат между прямыми с уравнениями y b |
и |
y b |
|||||||||||||||||||
(см. рис. 40). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть переменная x принимает отрицательные значения, |
и абсолютная |
|||||||||||||||||||||
величина | |
x | |
неограниченно возрастает. |
В этом случае говорят, что |
x . |
||||||||||||||||||
Запишем определение предела функции |
y f (x) при |
x символически. |
||||||||||||||||||||
Число |
|
b |
|
называется |
пределом |
функцииy f (x) |
при |
x , если |
||||||||||||||
|
0 |
|
|
|
0 |
|
|
M |
|
| f (x) |
|
|
|
|
|
lim f (x) b |
. |
|
|
|||
|
M |
|
x |
|
|
|
b | |
|
. В этом случае пишут x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
5354.ru |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Пусть x изменяется, принимая как положительные, так и отрицательные значения, абсолютная величина | x | неограниченно увеличивается. Тогда говорят, что x стремится к бесконечности, и пишут x . Число b называет-
ся пределом функции y f (x) |
при x , если для любого положительного |
|
числа |
найдётся такое число N 0 , что для всех x , абсолютная величина ко- |
|
торых | |
x | N , имеет место неравенство | f (x) b | , т. е. |
|
|
0 N 0 | x | N | f (x) b | . |
|
В этом случае пишут x |
. |
|
|
lim f (x) b |
|
Можно показать, что если существует последний предел, то существуют предыдущие два предела и все три равны между собой. И наоборот, если существуют предыдущие два предела и они равны, то существует третий, равный двум предыдущим.
§ 5. Предел функции при x x0 и его геометрический смысл.
Односторонние пределы
Пусть |
x0 – |
заданное число. Рассмотрим предел функции y f (x) , когда |
|
x x0 и |
x x0 . |
Число b называется пределом слева функции |
y f (x) при |
x x0 , если для любого числа 0 найдётся такое число 0, |
что для всех |
||
точек интервала x0 x x0 выполняется неравенство f x b , каким бы малым ни было. Сказанное можно записать символически в виде
0 0 (x0 x x0 ) | f (x) b | .
В этом случае пишут lim f (x) b. Так же, как для N в § 4, фигурирующая в
x x0 0
определении величина зависит от , т. е. является функцией от ( ( )) ,
и чем меньше , тем меньше . |
|
|
|
По аналогии дадим определение предела функции |
y f (x) |
справа при |
|
x x0 . Число b называется пределом функции y f (x) при x x0 |
справа, если |
||
0 0 (x0 x x0 ) | f (x) b | . |
|
||
В этом случае пишут |
lim f (x) b. |
|
|
x x0 0 |
|
|
|
Эти два предела |
называются односторонними |
пределами функции |
|
y f (x) . Теперь дадим определение двустороннего (обычного) предела функ-
79
5354.ru
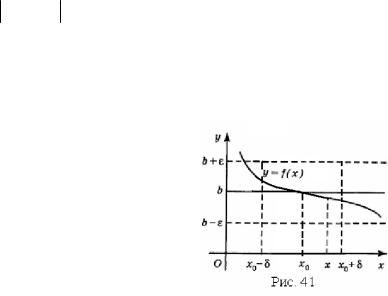
ции при x x0 (далее всегда под пределом функции при x x0 будем иметь ввиду именно этот двусторонний предел).
Число b называется (двусторонним) пределом функции y f (x) при x x0 , если для любого числа , каким бы малым оно ни было, найдётся такое число 0, что для всех точек интервала x0 x x0 , отличных от x0 , выполняется неравенство f x b , т. е.
0 0 (x0 x x0 ), x x0 | f (x) b | .
В этом случае пишут lim f (x) b.
x x0
Можно проверить, что если су-ществует последний предел, то существуют оба предыдущих одно- сто-ронних предела и все три предела равны между собой. И наоборот, если существуют оба односторонних предела и они равны друг другу, то существует двусторонний предел функции при x x0 , рав-
ный односторонним.
Выясним геометрический смысл двустороннего предела функции. Согласно определению, для всех точек интервала (x0 , x0 ), отличных от x0 , выполняется соотношение (2). Геометрически это означает, что если абсцисса x точки графика y f (x) лежит в интервале x0 , x0 , x x0 , то ордината f (x) этой точки лежит в интервале (2) (см. рис. 41). Следовательно, указанная точка лежит между прямыми y b и y b . Это относится к любой точке кривой y f (x) , абсцисса которой лежит в интервале (x0 , x0 ) и x x0 . Поэтому соответствующий участок графика лежит между вышеуказанными прямыми.
§ 6. Теоремы о пределах. Ограниченные функции
Все теоремы о пределах функции y f (x) будем доказывать для случая, когда x . В остальных случаях стремления x доказательства аналогичны.
Теорема 1. Если функция имеет предел при x , то этот предел будет единственным.
80
5354.ru
