
Мет.моделирования и прогнозирования эк-ки
.PDFИгровые модели |
|
|
|
|
|
|
|
|
81 |
Помимо двух записанных уравнений относительно a1* |
и a*2 до- |
||||||||
бавим уравнение, связывающее частоты a1* |
и a*2 : |
a1* a*2 1. |
|
||||||
Решая полученную систему трех уравнений с тремя неизвест- |
|||||||||
ными, находим a1* = 0.4; a*2 |
= 0.6; |
= 22/5. |
|
|
|
|
|
||
Найдем теперь оптимальную стратегию для игрока В. |
|
||||||||
Пусть |
стратегия |
для данного |
игрока |
задается |
вектором |
||||
B b1; b2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
* |
4.4, |
|
|
|
|
|
2b |
5b |
|
|||
|
|
|
|
|
1 |
|
2 |
|
|
Тогда имеем систему уравнений |
|
* |
|
* |
4.4, |
|
|||
6b1 |
4b2 |
|
|||||||
|
|
|
|
* |
|
|
* |
|
|
|
|
|
|
b1 |
b2 1. |
|
|||
|
|
|
|
|
|
|
|
|
|
Решая эту систему уравнений, состоящую из каких-нибудь двух |
|||||||||
уравнений, взятых из последней системы, получим b1* = 0.2; |
b2* = 0.8. |
||||||||
Следовательно, |
решением |
игры |
являются |
|
смешанные стратегии |
||||
A* 0.4; 0.6 |
и B* 0.2; |
0.8 , а цена игры |
= 4.4. |
|
|
||||
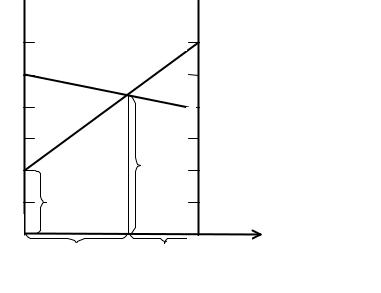
Дадим теперь геометрическую интерпретацию решения дан-
ной игры. Для этого на плоскости введем систему координат и на оси абсцисс отложим отрезок единичной длины A1A2 , каждой точке которого поставим в соответствие некоторую смешанную стратегию A a1; a2 a1; 1 a1 (рис.3.1). В частности, точке A1 0; 0 отвечает стратегия A1 и т. д.
В точках A1 и A2 восставим перпендикуляры и на полученных прямых будем откладывать выигрыш игрока А. На первом перпендикуляре (в данном случае он совпадает с осью ординат) отложим выигрыш игрока А при стратегии A1, а на втором – при стратегии A2 .
Если игрок A применяет стратегию A1 , то его выигрыш при
стратегии B1 игрока В равен 2, а при стратегии B2 |
он равен 5. Числам 2 |
|
и 5 на оси ординат соответствуют точки B1 и B2 . |
|
|
Если же игрок А применяет стратегию |
A2 , |
то его выигрыш при |
стратегии B1 игрока В равен 6, а при стратегии |
B2 |
он равен 4. Эти два |
числа определяют две точки B1' и B'2 на перпендикуляре, восстановлен-
ном в точке A2 .
82 |
Глава 3 |
Соединяя между собой точки B1, и B1' , B2 и B'2 , получим две
прямые, расстояние до которых от оси абсцисс определяет средний выигрыш при любом сочетании соответствующих стратегий.
Например, расстояние от любой точки отрезка B1 B1' до оси абсцисс определяет средний выигрыш 1 при конкретном cочетании стратегий A1 и A2 (с частотами a1 и a2 ) и стратегии B1 игрока B.
Это расстояние равно 2a1 6a2 1. Аналогично, средний вы-
игрыш при применении стратегии B2 определяется ординатами точек,
принадлежащих отрезку B2 B'2 .
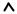 Выигрыш игрока А
Выигрыш игрока А
|
|
6 |
B1 |
` |
B2 |
|
M |
|
|
5 |
|
|
|
|
|
|
4 |
B2 |
` |
B1 |
|
|
|
|
Выигрыш |
|
|
|
|
2 |
|
|
|
|
|
при А1 |
|
A2 |
|
A1 |
|
|
|
|
|
|
|
|
|
0 |
a2 |
1-a2 |
1 |
Частота использования |
|
|
|
|
стратегии a2 |
Рис.3.1. Графическое решение задачи 2
Таким образом, ординаты точек, принадлежащих ломаной
B1M B'2 , определяют минимальный выигрыш игрока А при применении
им любых смешанных стратегий.
Эта минимальная величина является максимальной в точке M; следовательно, этой точке соответствует оптимальная стратегия
A* a1* ,a*2 , а ее ордината равна цене игры .
Координаты точки М находим как координаты точки пересече-
ния прямых B1 B1' и B2 B'2 . Соответствующие три уравнения имеют вид
Игровые модели |
|
83 |
||
2a* |
6a* |
, |
|
|
|
1 |
2 |
|
|
|
* |
* |
, |
|
5a1 |
4a2 |
|
||
* |
|
* |
|
|
a1 |
a2 1. |
|
||
|
|
|
|
|
Решая эту систему уравнений, получаем |
|
|||
a1* = 2/5; a*2 |
= 3/5; = 22/5 = 4,4. |
|
||
Аналогично находится оптимальная стратегия для игрока B. |
||||
Для ее определения имеем уравнения |
|
|||
2b* |
5b* |
4.4, |
|
|
|
1 |
2 |
|
|
* |
|
* |
|
|
b |
b 1. |
|
||
1 |
|
2 |
|
|
Решение этой системы: b1* 0.2, b*2 |
0.8 . |
|||
Следовательно, решением игры являются смешанные стратегии
A* 0.4;0.6 и B* 0.2;0.8 , а цена игры 4.4 .
Обобщая изложенные выше результаты нахождения решения игры 2 2, можно указать основные этапы нахождения геометрического решения игры 2 n или n 2.
1.Строят прямые, соответствующие стратегиям второго (первого) игрока.
2.Определяют нижнюю (верхнюю) границу выигрыша.
3.Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой.
4.Определяют цену игры и оптимальные стратегии.
|
|
Пример 3.3. Найти |
решение |
игры, заданной матрицей |
|||
|
7 |
9 |
8 |
|
|
|
|
C |
|
|
|
|
|
|
|
|
6 |
9 |
. |
|
|
|
|
|
10 |
|
|
|
|
||
|
|
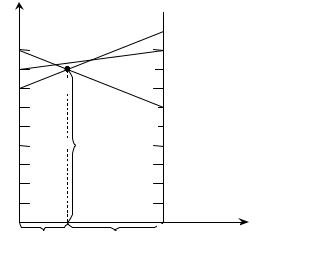
Решение. На рис.3.2 прямые B1B1' , B2B2' и B3B3' соответству- |
|||||
ют стратегиям, а ломаная B1KB2' |
– нижней границе выигрыша игрока В. |
||||||
|
|
Игра имеет решение |
|
|
|||
|
|
A* 2/ 3; 1/ 3 , |
B* 1/ 2; 1/ 2; |
0 , 8. |
|||
84 |
|
|
|
|
Глава 3 |
|
|
Выигрыш |
B1` |
||
|
|
игрока А |
|||
|
|
|
|
|
10 |
|
9 |
|
|||
B2 |
9 |
||||
B3 |
|
|
B3` |
||
B1 7 K
B2` 6

0 |
* |
* |
1 |
Частота использования |
a |
2 |
a 1 |
|
стратегии a2
Рис.3.2. Графическое решение задачи 3
3.4. СВЕДЕНИЕ ИГРОВЫХ МОДЕЛЕЙ К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим игру m n, определяемую матрицей
c |
c |
|
c |
|
||
11 |
12 |
|
1n |
|
||
c |
21 |
c |
c |
2n |
|
|
C |
22 |
|
|
. |
||
cm1 cm1 cmn
Для оптимальной стратегии первого игрока A* a1*,a*2, ,a*m и
|
m |
|
|
|
|
|
цены игры |
выполняется неравенство cija*i |
; |
j |
1,n . |
||
|
i 1 |
|
|
|
|
|
Предположим для определенности, что 0. Это всегда может быть достигнуто благодаря тому, что прибавление ко всем элементам матрицы С одного и того же постоянного числа K не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на K.
Разделив теперь обе части последнего неравенства на , полу-
чим:
m |
* |
|
|
|
|
cij |
ai |
1; |
j 1,n . |
||
|
|||||
i 1 |
|
|
|
|
|
Игровые модели |
|
|
|
|
|
|
|
85 |
||
|
a*i |
|
* |
|
|
|
|
|
|
|
Положим |
|
x |
. Tогда |
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
j 1,n |
; |
|
i |
|
. |
|
m |
|
|
|
|
|
|
||||
cijx*i |
1; |
x*i 0; |
1,m |
|||||||
i 1
m
Используя введенное обозначение, перепишем условие a*i 1
i 1
в виде
x*i 1 .
i1m
Так как первый игрок стремится получить максимальный выиг-
рыш, то он должен обеспечить минимум величине 1 . С учетом этого,
определение оптимальной стратегии первого игрока сводится к нахожде-
m
нию минимального значения функции F1 xi при условиях
|
|
|
|
|
|
i 1 |
m |
j |
|
; xi 0; |
i |
|
. |
cij xi 1; |
1,n |
1,m |
||||
i 1 |
|
|
|
|
|
|
Аналогичные рассуждения показывают, что определение оптимальной стратегии второго игрока сводится к нахождению макси-
|
|
|
|
|
|
|
|
|
|
n |
|
|
мального |
значения |
функции |
F2 yj |
при |
условиях |
|||||||
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
n |
|
|
i |
|
|
; yj 0; j 1,n |
. |
|
|
|||
cij yj |
1; |
|
1,m |
|
|
|||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
yj |
bj |
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, чтобы найти решение данной игры, определяемой матрицей С, нужно составить пару двойственных задач и найти их решение:
m
1. Найти минимальное значение функции F1 xi при условиях:
|
|
|
|
i 1 |
||
m |
j |
|
; xi 0; |
i |
|
. |
cij xi 1; |
1,n |
1,m |
||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
2. Найти максимальное значение функции F2 yj при условиях
j 1

86 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 3 |
n |
|
|
|
|
i |
|
|
; yj 0; j 1,n |
. |
|||||||||
cij yj |
1; |
1,m |
||||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя решение пары двойственных задач, получаем фор- |
||||||||||||||||||
мулы для определения стратегий и цены игры: |
|
|
|
|
|
|||||||||||||
* |
|
|
x* |
|
* |
|
|
* |
|
|
y*j |
|
* |
|
||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
||||||
ai |
|
|
|
|
xi |
; |
bj |
|
|
|
|
yj ; |
||||||
|
m |
* |
n |
* |
||||||||||||||
|
|
|
xi |
|
|
|
|
|
|
xj |
|
|
|
|
||||
|
|
i 1 |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
||
|
|
1 |
|
|
|
1 |
|
; |
i |
|
|
|
|
. |
||||
|
|
|
|
|
1,m; |
j 1,n |
||||||||||||
|
|
* |
|
m * |
|
|||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
yj |
|
xi |
|
|
|
|
|
|
|
|
|
|
|
||||
|
j 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
||
Итак, процесс нахождения решения игры с использованием методов линейного программирования включает следующие этапы:
1.Составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
2.Определяют оптимальные планы пары двойственных задач.
3.Используя соотношение между планами пары двойственных задач и оптимальными стратегиями и ценой игры, находят решение игры.
Пример 3.4. Два игрока А и В одновременно и не сговариваясь показывают один, два или три пальца. Выигрыш решает общее количество пальцев: если оно четное, то выигрывает А и получит у В сумму, равную этому числу; если нечетное, то, наоборот, А платит В сумму, равную этому числу. Определить стратегии поведения игроков.
Решение. Составим матрицу игры. В каждой партии у каждого игрока три стратегии: показать 1, 2 или 3 пальца. Поэтому имеем матрицу игры в виде:
|
В1 = 1 |
В2 = 2 |
В3 = 3 |
i |
А1 = 1 |
2 |
-3 |
4 |
-3 |
А2 = 2 |
-3 |
4 |
-5 |
-5 |
А3 = 3 |
4 |
-5 |
6 |
-5 |
j |
4 |
4 |
6 |
|
Здесь αi minсij ; |
βj maxсij . |
|
|
|
|
j |
i |
|
|
|
|
|
|
|
|
|
3 |
Нижняя цена игры игрока А равна величине. min maxс |
|||||
|
i |
|
j |
|
|
|
|
|
|
||
Это означает, что при разумном, осторожном поведении мы гарнируем, что не проиграем больше, чем 3. Нижняя цена игры игрока В
(верхняя цена игры для игрока А) |
|
|
|
|
4 |
. Оптимальные |
max minc |
|
|||||
|
j |
i |
ij |
|
|
|

Игровые модели |
87 |
стратегии игроков возможны в смешанных стратегиях A* a1*,a*2,a*3 и
B* b1*,b*2,b3* . Для оптимальных стратегий имеем соотношения:
m |
|
|
|
|
|
m |
|
cija*i |
; |
j 1,n ; |
a*i |
1; |
|||
i 1 |
|
|
|
|
|
i 1 |
|
n |
|
|
|
|
|
n |
|
cijb*j ; |
i 1,m ; |
b*j 1 |
|||||
j 1 |
|
|
|
|
|
j 1 |
|
Для того, чтобы выполнялось условие > 0, прибавим ко всем элементам матрицы С число K =10, что не изменит оптимальных стратегий, а лишь увеличит цену игры на K =10, и сделаем замены переменных
xi a*i .
Имеем задачу линейного программирования для стратегий пер-
|
|
|
|
m |
|
|
m |
|
|
|
|
|
|
|
вого |
игрока: |
F1 xi min |
при |
стратегиях |
cij xi 1; |
|
j 1,n; |
|||||||
|
|
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|
xi 0; |
i |
1,m |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для второго игрока, сделав замену переменных yj |
bj |
полу- |
||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
чаем |
|
задачу |
F2 yj max |
при |
условиях |
cij y j |
1;i 1,m; |
|||||||
|
|
|
|
j 1 |
|
|
j 1 |
|
|
|
|
|
|
|
yj 0; j 1,n.
Оптимальные стратегии игроков определяются соотношениями:
* |
|
x*i |
|
* |
|
* |
|
y*j |
|
* |
|
1 |
|
|
1 |
|
. |
ai |
|
|
|
xi |
; |
bj |
|
|
|
y j ; |
|
|
|
|
|
|
|
m |
* |
n |
* |
n |
* |
m |
* |
||||||||||
|
|
xi |
|
|
|
|
y j |
|
|
yj |
|
xi |
|||||
|
|
i 1 |
|
|
|
|
|
j 1 |
|
|
|
j 1 |
|
|
i 1 |
|
|
В нашем случае имеем задачи линейного программирования, симметричные для обоих игроков.
Для первого игрока имеем следующую модель:
3
F1 xi min; i 1
x |
|
|
|
|
|
|
0; |
i 1,3 |
|||||
i |
|
|
|
14x 1 |
||
12x 7x |
2 |
|||||
|
1 |
|
3 |
|||
7x1 14x2 5x3 1 |
||||||
|
|
|
|
16x3 1 |
||
14x1 5x2 |
||||||
88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 3 |
Решение этой задачи: |
|
|
|
|
|
|
||||||||
* |
|
1 |
* |
1 |
|
|
* |
1 |
|
|
|
|||
x1 |
|
|
; x2 |
|
|
|
; |
x3 |
|
|
; |
|
|
|
40 |
20 |
40 |
|
|
||||||||||
|
|
3 |
1 |
|
1 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
10. |
|
|
|
||
|
xi |
|
|
|
|
|
||||||||
|
i 1 |
|
|
10 |
|
|
|
|
|
|
||||
Тогда A* 0.25; |
0.5; |
0.25 , |
B* 0.25; 0.5; |
0.25 . |
||||||||||
КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 3
1.Дайте понятие игры и поясните ее экономикоматематическую постановку. Приведите примеры.
2.Приведите классификацию игр и поясните их особенности.
3.Что такое минимаксная и максиминная стратегии игроков?
4.Что такое чистая и смешанная стратегии игроков?
5.В чем заключается геометрическое решение игровых задач?
6.Покажите способ сведения игровых задач к задачам линейного программирования.
ЗАДАНИЕ К ГЛАВЕ 3
Исследовать решение трех игровых задач. Требуется:
1.Найти графическое решение игры № 1 (табл.3.1).
2.Найти решение игры № 2.
3.Составить двойственную пару задач линейного программирования (прямую и обратную) для игры № 3. Указать возможные пути решения этих задач, их содержательный смысл.
4.Проанализировать результаты. Дать содержательную трактовку (физическую интерпретацию) имеющихся данных и полученных решений.
Варианты заданий приведены в табл.3.1.
Таблица 3.1
Варианты исходных данных (матрицы платежей)
№ |
|
Игра № 1 |
|
|
|
Игра № 2 |
|
|
|
Игра № 3 |
|||||
вар. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
1 |
7 |
3 |
3 |
9 |
2 |
12 |
3 |
19 13 |
||||
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
12 |
6 |
8 14 |
7 |
16 8 14 |
||||
|
6 |
7 |
4 |
3 |
|
||||||||||
|
|
|
|
5 |
2 |
4 |
8 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
19 |
5 11 |
|||||
|
9 |
2 |
1 |
4 |
|
3 |
7 |
9 2 |
|
8 |
3 |
9 12 |
|||
2 |
|
|
|
|
|
|
|
6 |
|
||||||
|
|
|
|
|
|
|
5 |
6 8 14 |
|
7 |
8 14 |
||||
|
|
|
5 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
10 |
|
2 5 8 |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
4 |
|
|
9 |
5 1 |
|||
Игровые модели |
89 |
№ |
|
Игра № 1 |
|
|
Игра № 2 |
|
Игра № 3 |
|
|||||||
вар. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
9 |
8 |
7 |
10 |
13 |
19 |
22 |
3 |
7 |
9 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
17 |
16 |
18 |
19 |
5 |
6 |
8 |
14 |
|
|
6 |
5 |
4 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
2 5 8 |
|
||||||
|
|
|
|
|
|
|
9 |
12 25 11 |
4 |
|
|||||
|
4 |
6 |
1 |
7 |
3 |
3 |
9 2 |
2 |
3 9 13 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
11 6 |
8 14 |
7 |
16 8 4 |
|||||
|
6 |
5 |
4 |
3 |
|
||||||||||
|
|
|
|
2 |
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
4 |
0 8 |
6 |
2 11 |
|||||
|
8 |
2 |
8 |
7 |
102 |
13 |
111 |
212 |
8 |
3 |
9 |
12 |
|||
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
|
|
|
|
|
137 |
126 |
120 |
129 |
7 |
6 |
8 |
14 |
|
|
6 |
5 |
1 |
2 |
|
||||||||||
|
|
|
|
92 |
115 |
|
|
2 |
5 |
1 |
|
||||
|
|
|
|
|
|
|
49 |
151 |
9 |
|
|||||
|
9 |
12 |
1 |
4 |
90 |
83 |
119 |
212 |
1 |
7 |
28 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
||||||
6 |
|
|
|
|
|
|
107 |
106 |
108 |
149 |
7 |
12 |
8 |
|
21 |
|
|
5 |
8 |
|
|
|
|||||||||
|
3 |
10 |
|
102 |
35 |
|
|
31 |
0 |
|
|
||||
|
|
|
|
|
|
|
129 |
211 |
0 |
|
1 |
||||
|
2 |
1 |
8 |
7 |
3 |
7 |
9 |
2 |
31 |
37 |
29 |
12 |
|||
|
|
|
|
|
|
|
|
|
|
||||||
7 |
|
|
|
|
|
|
5 |
6 8 14 |
7 |
62 8 14 |
|||||
|
6 |
5 |
4 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
4 |
2 5 8 |
9 |
2 51 1 |
|||||
|
2 |
1 |
2 |
|
7 |
190 |
83 |
119 |
212 |
2 |
3 |
19 |
13 |
||
8 |
|
|
106 |
108 |
|
|
16 |
8 |
|
|
|||||
|
|
|
|
|
|
107 |
149 |
7 |
4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 5 |
1 3 |
102 |
35 |
2 |
52 |
|
||||||||
|
|
|
|
|
|
|
129 |
211 |
9 |
11 |
|||||
|
9 |
12 |
1 |
4 |
2 |
9 |
6 |
9 |
12 |
3 |
19 |
13 |
|||
|
|
|
|
|
|
|
|
|
|
||||||
9 |
|
|
|
|
|
|
15 |
12 8 14 |
8 |
16 8 4 |
|||||
|
|
5 |
8 |
|
|
||||||||||
|
3 |
10 |
|
9 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
7 |
5 8 |
19 |
2 5 11 |
|||||
|
2 |
1 |
8 |
7 |
2 |
7 |
6 9 |
0 |
8 9 3 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
10 |
|
|
|
|
|
|
15 |
26 |
8 |
14 |
15 |
6 |
8 |
14 |
|
|
|
|
|
|
|
||||||||||
|
0 5 |
4 3 |
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
4 |
7 8 |
4 |
12 5 8 |
|||||
|
2 |
1 |
8 |
7 |
1 |
7 6 2 |
2 |
3 19 3 |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
11 |
|
|
|
|
|
|
5 |
6 8 14 |
7 |
1 8 |
|
4 |
|||
|
6 |
5 |
4 |
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 |
2 5 0 |
9 |
2 0 11 |
|||||
90 |
Глава 3 |
№ |
|
Игра № 1 |
|
|
|
Игра № 2 |
|
|
|
Игра № 3 |
|
|||||||
вар. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
1 |
7 |
|
5 3 |
9 2 |
|
2 |
3 9 13 |
||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
11 6 |
8 14 |
|
7 |
16 8 4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 7 4 3 |
|
|
|
|
|
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
4 2 |
0 8 |
|
6 |
2 11 |
||||||
|
2 |
1 |
8 |
9 |
3 3 |
9 |
2 |
1 |
3 5 12 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13 |
|
|
|
|
|
|
12 6 |
8 14 |
7 |
0 8 14 |
||||||||
|
7 |
5 |
4 |
3 |
|
|||||||||||||
|
|
|
|
5 2 |
4 |
8 |
|
|
2 51 1 |
|
||||||||
|
|
|
|
|
|
|
|
|
9 |
|
||||||||
|
4 |
2 |
6 |
7 |
|
1 7 |
6 2 |
|
1 7 2 |
12 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
14 |
|
|
|
|
|
|
|
5 6 |
8 14 |
|
7 |
0 8 8 |
||||||
|
6 |
5 |
4 |
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 3 1 |
|
||||||
|
|
|
|
|
|
|
|
3 2 |
5 0 |
|
9 |
|
||||||
|
9 |
2 |
7 |
4 |
|
3 7 |
9 2 |
|
2 |
3 19 3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
15 |
|
|
|
|
|
|
|
5 6 |
8 9 |
|
7 |
1 8 |
4 |
|||||
|
|
5 |
8 |
|
|
|
|
|||||||||||
|
3 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
4 2 |
5 8 |
|
9 |
2 0 11 |
||||||
|
9 |
12 |
1 |
4 |
3 3 |
9 |
2 |
1 |
3 5 |
12 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16 |
|
|
|
|
|
|
12 6 |
8 14 |
7 |
0 |
8 |
|
4 |
|||||
|
|
15 |
8 |
|
|
|
||||||||||||
|
3 |
10 |
|
5 |
|
2 |
4 |
8 |
|
|
2 23 |
|
||||||
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|||||||
|
4 |
9 |
1 |
7 |
3 |
|
3 |
9 |
2 |
12 |
3 |
19 |
13 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
17 |
|
|
|
|
|
|
12 |
|
6 |
8 |
14 |
7 |
16 |
8 |
14 |
|||
|
6 |
5 |
4 |
3 |
|
|
||||||||||||
|
|
|
|
5 2 |
4 |
8 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
19 |
2 5 11 |
||||||||
|
9 |
12 |
1 |
4 |
90 |
|
83 |
79 |
22 |
8 |
3 |
9 |
12 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
18 |
|
|
|
|
|
|
197 |
106 |
108 |
149 |
7 |
6 |
8 |
14 |
||||
|
|
5 |
8 |
|
|
|||||||||||||
|
3 |
10 |
|
|
|
72 |
35 |
|
|
|
2 |
5 |
|
|||||
|
|
|
|
|
|
|
129 |
|
211 |
9 |
1 |
|||||||
|
2 |
1 |
8 |
7 |
10 |
|
13 |
19 |
22 |
3 |
7 |
9 |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
19 |
|
|
|
|
|
|
17 |
|
16 |
18 |
19 |
5 |
6 |
8 |
14 |
|||
|
6 |
5 |
4 |
3 |
|
|
||||||||||||
|
|
|
|
9 12 |
25 11 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
4 |
2 5 8 |
||||||||
|
4 |
2 |
1 |
7 |
|
3 |
3 |
9 2 |
|
0 |
8 9 3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
20 |
|
|
|
|
|
|
|
11 |
6 |
8 14 |
|
15 |
6 |
8 |
14 |
|||
|
6 |
5 |
4 |
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 5 8 |
|
||||||
|
|
|
|
|
|
|
|
4 2 |
0 8 |
|
4 |
|
||||||
