
Мет.моделирования и прогнозирования эк-ки
.PDF
Оптимизационные модели в торговой и коммерческой деятельности |
31 |
|
||||||||||||
Если |
|
для |
|
|
некоторого |
опорного |
плана |
|||||||
X* ( x*ij ); (i 1,m |
; |
|
|
|
|
транспортной |
задачи существуют |
такие |
||||||
j 1,n) |
||||||||||||||
числа 1, 2, …, m, 1, 2, …, n, что |
|
|
|
|||||||||||
|
j |
i |
cij |
|
при |
xij > 0 |
|
(2.10) |
||||||
|
j |
i |
cij |
|
при |
xij = 0 |
|
(2.11) |
||||||
для всех |
|
|
|
и j |
|
|
то X* (x*ij ) – оптимальный план |
|||||||
i 1,m |
|
1,n, |
||||||||||||
транспортной задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Числа i и j (i 1,m; j 1,n) называются потенциалами со-
ответственно пунктов отправления и пунктов потребления. Сформулированные условия позволяет построить алгоритм на-
хождения решения транспортной задачи. Он состоит в следующем. Пусть найден опорный план транспортной задачи. Для каждого
из пунктов отправленной назначения определяют потенциалы i и
j |
(i 1,m; j 1,n). Эти числа находят из системы уравнений |
|
|
j i cij |
(2.12) |
где cij – тарифы, стоящие в заполненных клетках опорного плана таблицы условий задачи.
Так как число заполненных клеток опорного плана равно n + m – 1 то система (2.12) с n + m неизвестными содержит n + m – l уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например 1 = 0, и найти последовательно из уравнений (2.12) значения остальных неизвестных.
После того как все потенциалы найдены, для каждой из свободных клеток определяют числа ij j i cij .
Если среди чисел ij нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клеткиij > 0, то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых ij > 0, и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.
Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых клеток и связанных с заполненной так называемым циклом.
Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках табли-
32 |
Глава 2 |
цы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце.
Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных с данной свободной клеткой. Это перемещение производят по следующим правилам:
1)каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке – знак плюс, а всем остальным клеткам – поочередно знаки минус и плюс (будем называть эти клетки минусовыми и плюсовыми);
2)в данную свободную клетку переносят меньшее из чисел xij, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел xij, считается свободной.
В результате указанных выше перемещений грузов в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи.
Описанный выше переход от одного опорного плана транспортной задачи к другому ее опорному плану называется сдвигом по циклу пересчета.
При сдвиге по циклу пересчета число занятых клеток остается неизменным и равным n + m – 1. При этом если в минусовых клетках имеется два (или более) одинаковых числа xij, то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками).
Полученный новый опорный план транспортной задачи проверяют на оптимальность. Для этого определяют потенциалы пунктов от-
правления и назначения и находят числа ij j i cij для всех сво-
бодных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.
Оптимизационные модели в торговой и коммерческой деятельности |
33 |
Из изложенного выше следует, что процесс нахождения решения транспортной задачи методом потенциалов включает следующие
этапы:
1.Находят опорный план. При этом число заполненных клеток должно быть равным n + m – 1.
2.Находят потенциалы j и i соответственно пунктов назначения и отправления.
3.Для каждой свободной клетки определяют число ij. Если среди чисел ij нет положительных, то получен оптимальный план транспортной задачи; если же они имеются, то переходят к новому опорному плану.
4.Среди положительных чисел ij выбирают максимальное, строят для свободной клетки, которой оно соответствует, цикл пересчета
ипроизводят сдвиг по циклу пересчета.
5.Полученный опорный план проверяют на оптимальность, т.е. снова повторят все действия начиная с этапа 2.
Примечание. При определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать в этом случае зацикливания, следует соответствующие нулевые элементы опорного плана заменить сколь угодно малым положи-
тельным числом и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать равным нулю.
Пример 2.3. Для транспортной задачи, исходные данные которой приведены в табл.2.4, найти оптимальный план.
|
Исходные данные задачи |
|
Таблица 2.4 |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Пункты |
|
|
Пункты назначения |
|
Запасы |
|||
отправления |
B1 |
|
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|||||
A1 |
1 |
2 |
|
4 |
|
1 |
|
50 |
30 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A2 |
2 |
3 |
10 |
1 |
10 |
5 |
10 |
30 |
|
|
|
|
|
||||
|
|
|
|
|
|
|||
A3 |
3 |
2 |
|
4 |
|
4 |
10 |
10 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Потребности |
30 |
|
30 |
|
10 |
|
20 |
90 |
Решение. Сначала, используя метод северо-западного угла, находим опорный план задачи. Этот план записан в табл.2.4.
Найденный опорный план проверяем на оптимальность. В связи с этим находим потенциалы пунктов отправления и назначения.
Для определения потенциалов получаем систему, содержащую шесть уравнений с семью неизвестными
1 1 1, |
2 1 2, |
2 2 3, |
3 2 1, |
4 2 4, |
4 3 4. |
34 |
|
|
|
|
|
Глава 2 |
Полагая 1 = 0, находим 1=1, 2=2, 2= -1, 3=0, 4=4, 3=0. |
||||||
Для |
каждой |
свободной |
клетки |
вычисляем |
число |
|
ij j i cij : |
|
|
|
|
|
|
13 4, 14 3, 21 32 0, |
31 2, 33 4. |
|
||||
Найденные числа записываем их в каждую из свободных клеток табл. 2.5.
Так как среди чисел ij имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел ij являются14 = 3, поэтому для данной свободной клетки строим цикл пересчета (табл.2.5) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках равно 10. Клетка, в которой находится это число, становится свободной в новой табл. 2.5.
Таблица 2.5
Промежуточные результаты решения транспортной задачи
Пункты |
|
Пункты назначения |
|
|
Запасы |
|
отправления |
B1 |
B2 |
B3 |
B4 |
|
|
|
|
|||||
A1 |
1 |
2 |
4 |
1 |
|
50 |
30 |
-20 |
-4 |
|
+3 |
||
|
|
|
||||
A2 |
2 |
3 |
1 |
5 |
|
30 |
0 |
+10 |
10 |
|
-10 |
||
|
|
|
||||
A3 |
3 |
2 |
4 |
4 |
|
10 |
-2 |
0 |
-4 |
|
10 |
||
|
|
|
||||
Потребности |
30 |
30 |
10 |
20 |
|
90 |
Другие числа в табл. 2.5 получаются так: к числу 10, стоящему в плюсовой клетке табл.2.5, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл.2.5. Клетка на пересечении строки A2 и столбца B4 становится свободной.
После этих преобразований получаем новый опорный план
(табл. 2.6).
Таблица 2.6
Новый опорный план решения транспортной задачи
Пункты |
|
Пункты назначения |
|
|
Запасы |
|
отправления |
B1 |
B2 |
B3 |
B4 |
|
|
|
|
|||||
A1 |
1 |
2 |
2 |
1 |
|
50 |
30 |
-20 |
-2 |
|
+10 |
||
|
|
|
||||
A2 |
2 |
3 |
1 |
5 |
|
30 |
0 |
10 |
10 |
|
-3 |
||
|
|
|
||||
A3 |
3 |
2 |
4 |
4 |
|
10 |
+1 |
+3 |
-1 |
|
-10 |
||
|
|
|
||||
Потребности |
30 |
30 |
10 |
20 |
|
90 |
Оптимизационные модели в торговой и коммерческой деятельности |
35 |
Этот план проверяем на оптимальность. Снова находим потенциалы пунктов отправления и назначения. Для этого составляем следующую систему уравнений:
1 1 1, |
2 1 2, |
4 1 1, |
2 2 3, |
3 2 1, |
4 3 4. |
Полагаем 1 = 0, получаем 1 = 4 = 1, 2 = 2, 3 = 0, 3 = -3, 2 = - 1. Для каждой свободной клетки вычисляем число ij.
Имеем: 13 |
2, 21 0, 24 |
3, 31 |
1, 32 |
3, 33 |
1. |
||||||
Видим, что данный план перевозок не является оптимальным. |
|||||||||||
Поэтому переходим к новому опорному плану (табл. 2.7). |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Таблица 2.7 |
||
Улучшенный опорный план решения транспортной задачи |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
Пункты |
|
|
Пункты назначения |
|
|
|
Запасы |
||||
отправления |
|
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
A1 |
1 |
|
2 |
|
4 |
|
1 |
|
|
50 |
|
|
30 |
0 |
|
-4 |
|
|
20 |
|
|
||
|
|
|
|
|
|
|
|
||||
A2 |
2 |
|
3 |
|
1 |
|
5 |
|
|
30 |
|
|
0 |
20 |
|
10 |
|
|
-3 |
|
|
||
|
|
|
|
|
|
|
|
||||
A3 |
3 |
|
2 |
|
4 |
|
4 |
|
|
10 |
|
|
-2 |
10 |
|
-4 |
|
|
-3 |
|
|
||
|
|
|
|
|
|
|
|
||||
Потребности |
|
30 |
30 |
|
10 |
|
20 |
|
|
90 |
|
Сравнивая разности j i новых потенциалов, отвечающих
свободным клеткам табл. 2.10, с соответствующими числами cij, видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующих чисел cij.
Следовательно, получен оптимальный план:
|
30 |
0 |
0 |
20 |
|
|
X* |
|
|
20 |
10 |
0 |
|
0 |
. |
|||||
|
|
0 |
10 |
0 |
0 |
|
|
|
|
||||
При данном плане стоимость перевозок составляет величину
S = 1 30 + 2 0 + 1 20 + 3 20 + 1 10 + 2 10 = 140.
Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке
1. При некоторых реальных условиях перевозки груза из определенного пункта отправления Ai в пункт назначения Bj не могут быть осуществлены.
Для определения оптимальных планов таких задач предполагают, что тариф перевозки единицы груза из пункта Ai в пункт Вj является
36 |
Глава 2 |
сколь угодно большой величиной М, и при этом условии известными методами находят решение новой транспортной задачи.
При таком предположении исключается возможность (при оптимальном плане транспортной задачи) перевозить груз из пункта Ai в пункт Вj. Такой подход называют запрещением перевозок или блокированием соответствующей клетки таблицы данных транспортной задачи.
2. В отдельных транспортных задачах дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза.
Пусть, например, из пункта отправления Ai в пункт назначения Вj требуется обязательно перевести dij единиц груза. Тогда в клетку таблицы данных транспортной задачи, находящуюся на пересечении строки Ai и столбца Вj, записывает указанное число ij и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом перевозок М.
Для полученной таким образом новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи.
3. Иногда требуется найти решение транспортной задачи, при котором из пункта отправления Ai в пункт назначения Вj должно быть завезено не менее заданного количества груза ij.
Для определения оптимального плана такой задачи считают, что запасы пункта Ai и потребности пункта Вj меньше фактических на ij единиц.
После этого находят оптимальный план новой транспортной задачи, на основании которого и определяют решение исходной задачи.
4. В некоторых транспортных задачах требуется найти оптимальный план перевозок при условии, что из пункта отправления Ai в пункт назначения Вj перевозится не более чем ij единиц груза, т.е.
xij ij . |
(2.13) |
Сформулированную задачу можно решить так.
Втаблице исходных данных задачи для каждого j-го ограничения (2.13) предусматривают дополнительный столбец, т.е. вводят дополнительный пункт назначения.
Вданном столбце записывают те же тарифы, что и в столбце Вj, за исключением тарифа, находящегося в i-й строке.
Вдополнительном столбце в этой строке тариф считают равным некоторому сколь угодно большому числу М. При этом потребности
пункта Вj считают равными ij, а потребности вновь введенного пункта назначения полагают равными bj – ij.
Оптимизационные модели в торговой и коммерческой деятельности |
37 |
Решение полученной транспортной задачи может быть найдено методом потенциалов, и тем самым будет определен оптимальный план или установлена неразрешимость исходной задачи. Заметим, что исходная транспортная задача разрешима лишь в том случае, когда для нее существует хотя бы один опорный план.
Если в результате составления плана поставок все имеющиеся запасы пунктов отправления распределены и потребности в пунктах назначения удовлетворены, то получен опорный план транспортной задачи.
Если в какой-то строке (а следовательно, и в столбце) остался нераспределенный остаток, равный d, то вводят дополнительный пункт назначения и дополнительный пункт отправления с потребностями и запасами, равными d.
В клетке, находящейся на пересечении столбца дополнительного пункта назначения и строки дополнительного пункта отправления, тариф считают равным нулю.
Во всех остальных клетках данной строки и столбца тарифы полагают равными некоторому сколь угодно большому числу М.
Полученную в результате этого транспортную задачу решают методом потенциалов. После конечного числа шагов либо устанавливают, что исходная задача не имеет опорного плана, либо находят ее оптимальный план.
При этом ( x*ij ) – оптимальный план исходной задачи, если
|
при |
* |
j i cij 0 |
xij 0, |
|
|
при |
x*ij ij , |
j i cij 0 |
||
|
при |
* |
j i cij 0 |
0 xij ij . |
|
|
|
|
2.4. СИМПЛЕКСНЫЙ МЕТОД
Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какойнибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть требуется найти максимальное значение функции
F c1x1 c2x2 cnxn
при условиях
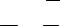
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 2 |
x1 a1m 1xm 1 a1nxn b1, |
|||||||||||||||
x |
2 |
a |
2m 1 |
x |
m 1 |
a |
|
x |
n |
b , |
|||||
|
|
|
|
|
|
2n |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
m |
a |
mm 1 |
x |
m 1 |
a |
|
x b |
|||||||
|
|
|
|
|
|
|
mn n |
m, |
|||||||
xj 0 j 1,n .
Здесь aij ,bi и cj i 1,m;j 1,n – заданные постоянные числа
m n; bi 0 .
Векторная форма данной задачи имеет следующий вид: найти максимум функции
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F cjxj max |
|
|
|
|
|
|
(2.13) |
||||||
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
при условиях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x1A1 x2A2 |
xmAm xnAn B, |
|
|
(2.14) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xj 0 |
j |
|
, |
|
|
(2.15) |
|||
|
|
|
|
|
|
|
|
|
|
|
1,n |
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
0 |
a1m 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
0 |
|
1 |
|
0 |
a2m 1 |
||||||||||||
|
|
|
; A2 |
; ; Am ; Am 1 |
|
|
; ; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
amm 1 |
|
||||||
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1n |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
A |
a2n ; B b2 . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
mn |
|
m |
|
|
|
|
|
|
|
|
||||
|
План |
X x1;x2; ;xn |
называется опорным планом задачи |
|||||||||||||||||
линейного программирования, если система векторов |
A1,A2, ,An, вхо- |
|||||||||||||||||||
дящих |
в |
|
разложение |
|
|
(2.14) |
с |
|
|
положительными величинами |
||||||||||
xj 0 |
j |
|
|
, линейно независима. |
Опорный план называется невы- |
|||||||||||||||
1,n |
||||||||||||||||||||
рожденным, если он содержит ровно m положительных компонент, иначе – вырожденным.
Так как b1A1 b2A2 bmAm B, то вектор X b1;b2; ;bm;0; ;0 является опорным планом данной задачи (последние n-m компонент вектора Х равны нулю).

Оптимизационные модели в торговой и коммерческой деятельности |
39 |
Этот план определяется системой единичных |
векторов |
A1,A2, ,Am, которые образуют базис m-мерного пространства. По-
этому каждый из векторов A1,A2, ,An, а также вектор B могут быть представлены в виде линейной комбинации векторов данного базиса.
m |
|
|
Пусть Aj xij Ai j 1,n . |
|
|
i 1 |
j 1,n ; |
|
m |
j zj cj |
|
Положим zj cixij |
||
i 1
Так как векторы A1,A2, ,Am – единичные, то xij aij и
m
j ciaij cj. i 1
j 1,n .
m
zj ciaij , а i 1
|
Опорный план |
X* x1* , x2* , ;xm*; 0; 0; ; 0 |
задачи |
|||
(6.13) – (6.15) является |
оптимальным, если |
j 0 для |
любого |
|||
j j 1,n |
. |
|
|
|
|
|
|
Если k 0 для некоторого j = k и среди чисел aik i 1,m |
нет |
||||
положительных aik 0 , |
то целевая функция |
(2.13) |
задачи (2.13) – |
|||
(2.15) не ограничена на множестве ее планов. |
|
|
|
|
||
|
Если опорный план Х задачи (2.13) – |
(2.15) |
не вырожден и |
|||
k 0, но среди чисел aik есть положительные (не все aik 0 ), то су-
ществует опорный план X' такой, что F( X ) F( X ).
Сформулированные положения позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать в виде табл.6.8.
В столбце Сб этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса. В столбце B записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов Aj
представляют собой коэффициенты разложения этих векторов по векторам данного базиса.

40 |
Глава 2 |
В табл.2.8 первые m строк определяются исходными данными задачи, а показатели (m+1)-й строки вычисляют. В этой строке в столбце вектора B записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора Aj – значение
j zj cj.
Значение zj находится как скалярное произведение вектора
|
|
|
m |
|
|
Aj j |
1,m |
на вектор Cб c1;c2; ;cm : |
zj ciaij j 1,n . |
||
|
|
|
i 1 |
||
Значение F0 равно произведению вектора B на вектор Сб :
m
F0 cibi . i 1
После заполнения табл.2.8 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m + 1)-й строки таблицы. В результате может иметь место один из следующих трех случаев:
1) j 0 для j = m+1, m+2, ..., n (при j 1,m , zj = cj). Поэтому в данном случае числа j 0 для всех j от 1 до n;
2)j < 0 для некоторого j, и все соответствующие этому индексу величины aij 0 (i 1,m );
3)j < 0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел аij положительно.
В первом случае исходный опорный план является оптималь-
ным.
Во втором случае целевая функция не ограничена сверху на множестве планов.
В третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится.
Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов Aj, имеющий индекс j, для которогоj 0. Пусть, например, k < 0 и решено ввести в базис вектор Ak.
Для определения вектора, подлежащего исключению из базиса, находят min bi / aik для всех aik 0 . Пусть этот минимум достигается
при i = r. Тогда из базиса исключают вектор Ar, а число ark называют разрешающим элементом. Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.
