
Мет.моделирования и прогнозирования эк-ки
.PDFОптимизационные модели в торговой и коммерческой деятельности |
51 |
Следовательно, план выпуска продукции, включающий изготовление 8 изделий В и 20 изделий С, является оптимальным.
При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
Оптимальным планом производства продукции не предусматривается изготовление изделий А. Введение в план выпуска продукции изделий вида А привело бы к уменьшению указанной общей стоимости.
Это видно из 4-й строки столбца вектора A1 , где число 5 пока-
зывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 руб.
Решение данного примера симплексным методом можно было бы проводить, используя лишь одну таблицу (табл.2.14). В этой таблице последовательно записаны одна за другой все три итерации вычислительного процесса.
Таблица 2.14
Решение задачи симплекс-методом
i |
Базис |
Сб |
B |
9 |
10 |
|
16 |
0 |
0 |
0 |
x1 |
x2 |
|
x3 |
x4 |
x5 |
x |
||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
Первая итерация |
|
|
|
|
|||
1 |
x4 |
0 |
360 |
18 |
15 |
|
12 |
1 |
0 |
0 |
2 |
x5 |
0 |
192 |
6 |
4 |
|
8 |
0 |
1 |
0 |
3 |
x6 |
0 |
180 |
5 |
3 |
|
3 |
0 |
0 |
1 |
4 |
|
|
F0 0 |
-9 |
-10 |
|
-16 |
0 |
0 |
0 |
|
|
|
Вторая итерация |
|
|
|
|
|||
1 |
x4 |
0 |
72 |
9 |
9 |
|
0 |
1 |
-3/2 |
0 |
2 |
x3 |
16 |
24 |
3/4 |
1/2 |
|
1 |
0 |
1/8 |
0 |
3 |
x6 |
0 |
108 |
11/4 |
3/2 |
|
0 |
0 |
-3/8 |
1 |
4 |
|
|
384 |
3 |
-2 |
|
0 |
0 |
2 |
0 |
|
|
|
Третья итерация |
|
|
|
|
|||
1 |
x2 |
10 |
8 |
1 |
1 |
|
0 |
1/9 |
-1/6 |
0 |
2 |
x3 |
16 |
20 |
1/4 |
0 |
|
1 |
-1/18 |
5/24 |
0 |
3 |
x6 |
0 |
96 |
5/4 |
0 |
|
0 |
-1/6 |
-1/8 |
1 |
4 |
|
|
400 |
5 |
0 |
|
0 |
2/9 |
5/3 |
0 |
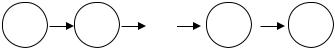
52 |
Глава 2 |
2.5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Динамическое программирование – это вычислительный метод для решения задач определённой структуры, в которых процесс принятия решений может быть разбит на этапы или шаги.
Нахождение решения конкретной задачи распадается на несколько шагов, на каждом из которых определяется решение некоторой частной задачи, обусловленной исходной задачей. Рассмотрим общую постановку задачи. Пусть имеется некоторый экономический процесс (система) S, который с течением времени может менять своё состояние. Состояние заключает в себе предысторию процесса и оно описывается с помощью того или иного количества переменных, называемых переменными состояния.
Предполагается, что можно управлять этим процессом, т.е. сознательно менять его состояние. Способ воздействия на процесс называется управлением. В качестве управления выступает некоторая величина X, численные значения которой влияют на изменение процесса. Например, процесс пополнения запасов товара на складе характеризуется текущим количеством товара, а объём завозимого товара на склад с некоторым интервалом поставок является управлением.
Пусть в результате воздействия управления X процесс переходит из некоторого начального состояния S0 в конечное состояние Sf . Предполагается, что управление X можно разбить на n шагов (например, по годам) и решение принимается последовательно на каждом шаге. Обозначим через Xk (k=1, 2…) управление на k-м шаге. Тогда совокупность X=(x1, x2, …xn) представляет управление процессом S, переводя его из состояния S0 в состояние Sf. Переменные xk не являются произвольными и должны удовлетворять некоторым ограничениям, вытекающим из специфики процесса.
Аналогично, обозначая через Sk – состояние процесса после k-го шага управления, получим последовательность состояний процесса
S0, S1,...Sk ...Sn 1,Sn Sf
Это можно представить в виде следующей графической схемы:
X1 |
S1 |
X2 |
… |
Xn-1 S |
Xn |
Sn |
S0 |
|
n- |
|
Рис. 2.1
Управление процессом производится с целью добиться лучшего значения некоторого показателя эффективности процесса, который представлен в виде целевой функции:
Z F(S0,x)
Сделаем два важных предположения:
Оптимизационные модели в торговой и коммерческой деятельности |
53 |
1. Будем считать, что состояние Sk процесса в конце k-го шага зависит только от предшествующего состояния Sk-1 и управления на k-м шаге xk и не зависит от того, каким образом процесс пришёл в состояние Sk-1, т.е. не зависит от предшествующих состояний S0, S1… и управлений x1, x2…xk-1. Это условие называют условием отсутствия последействия. Сформулированное требование можно записать в виде уравнений:
Sk =φk (Sk-1 , xk ),
которые называют уравнениями состояний процесса.
2.Если качество каждого из реализуемых управлений xk на k-
мшаге характеризовать значениями функции: Zk Фk(Sk 1,xk ), то
общий выигрыш за n шагов составит сумму показателей за каждый шаг:
n
Z Фk(Sk 1,xk ). k 1
Таким образом, целевая функция Z обладает свойством аддитивности.
Задача состоит в том, чтобы из множества возможных управле-
ний X ( X1,X2,...Xn ) найти такое управление |
X* ( X1* ,X*2 ,...X*n ) |
при котором целевая функция Z принимает экстремальное (максимальное или минимальное) значение, а процесс S переходит из начального состояния S0 в конечное состояние Sn=Sf.
Принцип оптимальности Беллмана.
Решение задачи методом динамического программирования
Вычислительная схема метода динамического программирования связана с принципом оптимальности, сформулированным американским математиком Беллманом. Этот принцип справедлив при выполнении условия отсутствия последействия и формулируется так: каково бы ни было состояние процесса перед очередным шагом, нужно выбрать управления на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был бы также оптимальным.
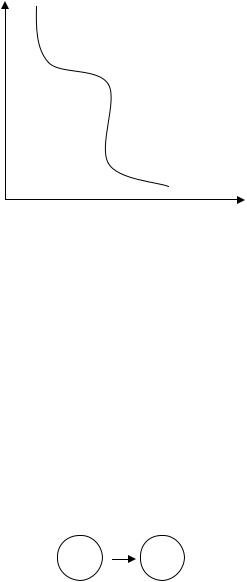
Дадим геометрическую интерпретацию принципа оптимальности. Пусть состояние процесса характеризуется точкой S на плоскости S1OS2.Эта точка под влиянием управления X её движением перемещается вдоль линии (траектории) из начального состояния S0 в конечное состояние.
54 |
Глава 2 |
S2
S0
1
Sk
Sn
O |
S1 |
Рис. 2.2
Принцип оптимальности утверждает, что если вся траектория оптимальна, то любой участок (напр. 2) также оптимален. Это означает, что если движение начинается из состояния Sk, то независимо от того, по какой траектории он попал в эту точку, его дальнейшее движение будет проходить по участку 2.
Из принципа оптимальности следует, что оптимальное управле-
ние X* ( X1* ,X*2 ,...X*n ) можно получить, если сначала найти опти-
мальное управление Xn* на последнем участке (на n-м шаге), затем на 2-
х последних шагах, на 3-х последних шагах и т.д. до первого шага. Поэтому решение любой задачи динамического программирова-
ния начинается от конца к началу, раньше всех определяется оптимальное управление на n-м шаге. Однако, неизвестно, чем закончится предпоследний (n-1)-й шаг. Очевидно, необходимо сделать какие-то предположения о состоянии Sn-1, и для этого предположения найти на n-ом шаге управления Xn, обеспечивающее максимум (или минимум) функции Фn(Sn-1, Xn). Такое управление называется условием оптимальности управления:
Sn-1 Xn Sn
Рис.2.3
Процесс из состояния Sn-1 под действием управления Xn переводится в конечное состояние Sn и выигрыш характеризуется значением

Оптимизационные модели в торговой и коммерческой деятельности |
55 |
функции Фn(Sn-1, Xn). Обозначим (для определённости) через Z*n(Sn 1 )
максимальное значение эффективности n-го шага при условии, что к его началу процесс находится в некотором состоянии Sn-1, а управление Xn
было оптимальным, т.е. Z*(Sn 1 ) maxФn(Sn 1,Xn ), Z* – условный
X n
максимальный выигрыш на n-м шаге.
Оптимальное управление Xn также зависит от состояния Sn-1. Будем обозначать условное оптимальное управление на n-м шаге:
X*n(Sn 1 ). Таким образом на последнем шаге мы найдём две функции
состояния Sn 1,Z*n(Sn 1 ): X*n(Sn 1 ).
Исследуем теперь два последних шага:
Sn-1 Xn-1 Sn-1 Xn Sn
Рис. 2.4
Для любых состояний Sn-2 к началу предпоследнего шага и управления на нём Xn-1 значение выигрыша на двух последних шагах
равно: Фn 1(Sn 2 ,Xn 1 ) Z*n(Sn 1 ). Согласно принципу оптимальности
Xn-1 следует выбирать так, чтобы суммарный выигрыш на 2-х последних шагах был бы также оптимальным. Тогда на предпоследнем шаге мы
получим оптимальный выигрыш Z*n 1(Sn 2 ), соответствующее опти-
мальное управление обозначается X*n 1(Sn 2 ). Итак:
Z*n 1(Sn 2 ) max Фn 1(Sn 1,Xn 1 ) Z*n(Sn 1 ) .
|
|
|
|
|
xn 1 |
|
|
|
|
|
|
Sn-1 |
можно |
найти |
из |
уравнения |
состояния: |
||
Sn 1 |
|
|
(Sn 2,Xn 1 ). |
Тогда |
Z*n 1(Sn 2 )зависит |
только |
от |
||
|
n 1 |
|
|
|
|
|
|
|
|
Sn 2 ,Xn 1. Рассуждая аналогично можно теперь получить функциональные уравнения Беллмана:
Z*k(Sk 1 ) max Фk (Sk 1,Xk ) Z*k 1(Sk ) , k=1, 2,…n-1. xk
Sk k(Sk 1,Xk )- уравнение состояния.
Функциональные уравнения Беллмана позволяют определить функции
Z*k(Sk 1 ), если известна следующая за ней функция Z*k 1(Sk ).
В результате решения задачи определяются две последовательности функций:
условные оптимальные выигрыши:
56 |
Глава 2 |
Z*n(Sn 1 ),Z*n 1(Sn 2 )...Z*2(S1 ),Z1*(S0 ).
условные оптимальные управления:
X*n(Sn 1 ),X*n 1(S*n 2 )...X*2(S1 ),X1*(S0 ). Начальное состояние S0 всегда известно. Решение задач происходит в следующем порядке:
1.Условные оптимальные выигрыши находятся по функцио-
нальным уравнениям Беллмана и уравнениям состояния от конца к началу. Получается ряд соотношений, где от
Z*n(Sn 1 ) переходят постепенно по шагам к состоянию
Z1*(S0 )- это и будет максимальный выигрыш задачи.
2.Условные оптимальные управления находятся в обратном порядке (от начала к концу). На первом шаге находили X1*(S0 ), на втором шаге по найденному X1* определим из уравнения
состояния: |
S* |
(S |
0 |
,X |
* |
) . |
Далее |
из |
S* |
найдём |
|
1 |
1 |
|
1 |
|
|
|
1 |
|
X*2 X*2 ,(S1* ) и т.д.
3.Планируется деятельность двух предприятий на 4 года. Имеется начальное количество ресурсов S0=10000 ед. Средства X, вложенные в предприятие №1 в начале года, в конце года дают прибыль f1=0,6 x. Вложенные средства x в течение года уменьшаются и возвращаются в конце года в размере q1(x)=0,7 x<x. Аналогично для предприятия №2 функция прибыли равна f2 =0,5 y, а возврата q2(y)=0,8 y<y.
4.В конце года все возращённые средства заново перераспределяются между двумя предприятиями, прибыль в производство не вкладывается и новые средства не поступают. Требуется распределить имеющиеся средства S0 между двумя предпри-
ятиями на 4 года так, чтобы суммарная прибыль за это время была максимальной.
Решение.
Пусть xk – количество средств, выделяемых первому предприятию в начале k-го года, тогда yk = Sk-1-xk – количество средств, вкладываемых во 2-е предприятие.
Используя конкретные данные примера, запишем для него уравнения состояния:
Sk q1( xk ) q2(Sk 1 xk ) 0,7xk 0,8(Sk 1 xk ) 0,85k 1 0,1xk .

Оптимизационные модели в торговой и коммерческой деятельности |
57 |
|
Целевая функция k-го шага запишется |
|
|
Фk(Sk 1,xk ) f1( xk ) f2(Sk 1 xk ) |
. |
|
0,6xk 0,5(Sk 1 xk ) 0,6xk 0,5Sk 1 0,5xk 0,5Sk 1 0,1xk |
||
|
Функциональные уравнения Беллмана сведутся к следующим:
Zk*(Sk 1 ) |
max 0,5Sk 1 0,1xk Zk* 1(Sk ) . |
|
0 xk Sk 1 |
Начнём расчёт с последнего шага(k=4).
Z4*(S3 ) |
max |
0,5S3 0.1x4 Z5*(S4 ) . |
|
|
|
0 x4 S3 |
|
Но на 5-й год средства не планируются, т.е. Z5*(S4 ) 0. Таким |
|||
образом: Z4*(S3 ) |
max |
0,5S3 0,1x4 . |
|
|
0 x4 S3 |
|
|
Обозначим |
функцию, |
стоящую в фигурных скобках через |
|
W4(x4). |
|
|
|
W4(x4)=0,5S3 0,1x4 – |
это линейная возрастающая функция: |
||
максимальное значение при x4=S3. W4(x4)
0,5 S3
S3
Рис. 2.5
Z*4(S3 ) 0,5S3 0,1S3 0,6S3 .
Переходим к следующему шагу 3-ему шагу (k=3).
Z3*(S2 ) |
max 0,5S2 0,1x3 Z*4(S3 ) |
max 0,5S2 0,1x3 0,6S3 . |
|
0 x3 S2 |
0 x3 S2 |
Используем уравнение состояния и выразим S3 через S2:
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 2 |
|
S3 0,8S2 0,1x3 , тогда |
|
|
|
|
|
|
|
|
||||||||||
|
Z3*(S2 ) |
|
max |
0,5S2 |
0,1x3 |
0,6(0,8S2 |
0,1x3 ) |
||||||||||||
|
|
|
|
|
|
0 x3 S2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
max |
|
0,5S2 0,1x3 |
0,48S2 0,06x3 |
max |
0,98S2 0,04x3 . |
|||||||||||||
|
0 x3 S2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 x3 S2 |
|
|
|||
|
Функция в фигурной скобке линейная и достигает максимума |
||||||||||||||||||
при x3=S2: Z3*(S2 ) 0,98S2 0,04S2 1,02S2 . |
|
|
|
|
|
||||||||||||||
|
Переходим к следующему шагу(k=2): |
|
|
|
|
||||||||||||||
Z2*(S1 ) |
max |
|
0,5S1 0,1x2 |
Z3*(S2 ) |
max |
0,5S1 |
0,1x2 1,02S2 . |
||||||||||||
|
0 x2 S1 |
|
|
|
|
|
|
|
0 x2 S1 |
|
|
|
|||||||
|
Используем теперь уравнение состояния для связи между S2 и |
||||||||||||||||||
S1: S2 0,8S1 0,1x2 , тогда |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Z |
* |
(S |
) |
|
max |
0,5S |
0,1x |
2 |
1,02(0,8S |
0,1x |
2 |
) |
||||||
|
|
2 |
|
1 |
|
|
0 x2 S1 |
1 |
|
|
|
1 |
|
|
|||||
|
max 0,5S1 0,1x2 0,816S1 0,102x2 |
max |
1,316S1 0,002x2 . |
||||||||||||||||
0 x2 S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x2 S1 |
|
|
|||
|
Функция в фигурных скобках линейная и достигает максимума |
||||||||||||||||||
при x2=0, т.е. Z* |
(S |
|
) 1,316S . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
Переходим к следующему шагу(k=1): |
|
|
|
|
||||||||||||||
Z1*(S0 ) |
|
max |
|
0,5S0 0,1x1 |
Z*2(S1 ) |
max |
0,5S0 |
0,1x1 1,316S1 |
|||||||||||
|
0 x1 S0 |
|
|
|
|
|
|
|
0 x1 S0 |
|
|
|
|
||||||
|
Используя уравнение состояния, получим связь между S1 и S0: |
||||||||||||||||||
S1 0,8S0 0,1x1 |
или |
0,5S |
|
|
|
|
|
|
|
0,1x |
|||||||||
|
Z |
* |
(S |
0 |
) |
|
max |
0 |
0,1x |
|
1,316(0,8S |
0 |
|||||||
|
|
1 |
|
|
|
0 x1 S0 |
1 |
|
|
|
|
1 |
|
||||||
max 0,5S0 0,1x1 1,0528S0 0,1316x1 |
max |
1,5528S0 0,0316x1 . |
|||||||||||||||||
0 x1 S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x1 S0 |
|
|
|
||
Эта функция достигает максимума при x1=0. Таким образом:
Z1*(S0 ) 1,5528S0 .
Мы получили оптимальную условную прибыль за 4 года:
Z |
* |
(S |
0 |
) 1,5528S |
0 |
1,5528 10000 15228 ед. Эту прибыль по- |
|
1 |
|
|
|
лучат оба предприятия.
Найдём теперь оптимальное условное управление, позволяющее добиться такой прибыли. В первый год для предприятия 1 средства вы-
деляются в количестве x1* 0. Таким образом, в первый год все средства S0=10000 вкладываются во 2-е предприятие.
Оптимизационные модели в торговой и коммерческой деятельности |
59 |
Состояние в конце года характеризуется величиной, получаемой из уравнения состояния: S1 0,8S0 0,1x1 0,8 10000 0 8000 ед.
Вначале второго года 1-е предприятие опять получает средства
вколичестве x2=0. Следовательно, опять все средства S1=8000 ед. получает 2-е предприятие. Состояние S2 в конце второго года получим из
уравнения состояния: S2 0,8S1 0,1x2 0,8 8000 0 6400 ед.
В начале 3-го года предприятие №1 получает средства x3=S2=6400 ед., а второе предприятие ничего не получает. Состояние процесса в конце 3-го года получается из уравнения состояния: S3 0,8S2 0,1x3 0,8 6400 0,1 6400 0,7 6400 4480 ед.
Вначале 4-го года предприятие №1 получает средства x4=S3=4480 ед., а второе предприятие не получает ничего. Таким образом, получаем следующее распределение средств между предприятиями
по годам:
для 1-го предприятия x*=(0;0;6400;4480); для 2-го предприятия x*=(10000;8000;0;0).
Суммарная максимальная прибыль составляет при этом 15528
ед.
2.6.НЕЛИНЕЙНОЕ И ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
Взадачах нелинейного программирования могут входить зависимости любого вида. Поэтому в общем виде задача нелинейного программирования состоит в определении максимального (минимального)
значения функции: Z f( x1,x2...) при условии, что её переменные удовлетворяют соотношениям:
g |
i |
(x |
,x |
2 |
...) b , |
(2.23.) |
|
или |
g |
1 |
,x |
i |
|||
|
i |
(x |
2 |
...) b . |
|
||
|
1 |
|
i |
|
|||
При этом предполагается, что известны функции переменных x1,x2..., а bi – заданные числа.
Класс задач нелинейного программирования шире класса задач линейного программирования. Например, производственные затраты в большинстве случаев не пропорциональны объёму выпуска, доход от реализации продуктов производства оказывается нелинейной функцией цен и т.д. Критериями в задачах оптимального планирования часто служит минимум прибыли, минимум себестоимости, минимум капитальных затрат и т.д.
60 |
Глава 2 |
Графическое решение задач нелинейного программирования
В отличие от задач линейного программирования с помощью нелинейного программирования можно найти точку локального оптимума, но нельзя установить, является ли она точкой глобального (абсолютного) оптимума или нет.
Процесс графического решения включает следующие этапы:
1.Находят область допустимых решений задачи, определяемую соотношением (2.23.).
2.Строят поверхность f( x1,x2...)=h – линии уровня (для пло-
ской задачи).
3.Определяют область наивысшего уровня (для случая max), или низшего уровня (для случая min).
4.Находят точку области допустимых решений, через которую проходит линия наивысшего (наинизшего) уровня и определяют в ней значение функции.
Для плоской задачи все эти процедуры сводятся к нахождению точки касания наинизшей или наивысшей линии уровня целевой функции (как функции 2-х переменных) и области допустимых решений.
Пример 1:
В области D, определяемой системой неравенств:
2x1 5x2 7, |
|
|
|
|
||||
|
|
x2 |
15, |
|
|
|
|
|
3x1 |
(2.24.) |
|
|
|
||||
4x |
7x |
2 |
71, |
|
|
|
||
|
1 |
|
|
|
|
|
|
|
x |
0;x |
2 |
0. |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Найти |
|
точку |
A( x10,x20 ), |
в |
которой |
функция |
||
f ( x1,x2 ) x12 ( x2 5)2 принимает наименьшее значение.
Решение:
1. Построим область D, заданную системой неравенств (2.24.) для чего из системы неравенств перейдём к равенствам и построим границы области допустимых решений.
2x1 5x2 7,3x1 x2 15,
4x1 7x2 71.
