Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4613 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Тульский Государственный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Мет.моделирования и прогнозирования эк-ки

.PDF
Скачиваний:
56
Добавлен:
10.05.2015
Размер:
2.61 Mб
Скачать
☆

Вероятностно-статистические модели

121

Второй определитель получается из первого вычеркиванием первой строки и последнего столбца.

7. Частные (парциальные) коэффициенты корреляции ис-

пользуются для оценки тесноты связи между двумя показателями из нескольких при элиминированном (исключенном) влиянии других показателей.

Пусть мы имеем три показателя X, Y, V. Частный коэффициент корреляции между X и Y при исключении V определяется через парные коэффициенты корреляции соотношением:

rxy|v

 

ryx ryvrxv

 

 

 

.

 

 

 

 

 

 

(1 r2

)(1 r

2

)

 

 

yv

xv

 

 

 

Абсолютные величины частных (парциальных) коэффициентов корреляции не могут быть больше величины коэффициента множественной корреляции.

8. Ранговые коэффициенты Спирмена и Кендалла оценивают степень тесноты связи между двумя ранговыми (качественными, порядковыми) показателями. Качественные показатели – это показатели, которые нельзя измерить точно, но с помощью которых можно сравнивать объекты между собой по степени улучшения или ухудшения этого показателя, т. е. ранжировать (упорядочивать) объекты.

Пусть имеем n объектов, которые характеризуются двумя качественными показателями А и В. Проранжируем объекты в порядке ухудшения качества по показателю А и присвоим объектам ранги xi, равные их порядковому номеру в этом ряду, т.е. xi = i. Затем при данном расположении объектов припишем ранг yi по признаку В. Тогда ранговый коэффициент корреляции Спирмена вычисляется по формуле

6

n

rc 1

 

( xi yi )2 .

n3 n

 

i 1

Допустим, что справа от y1 имеется k1 рангов больше чем y1, а

справа от y2 – k2 рангов больше чем y2 , ... , справа от yn 1 – kn 1

рангов больше, чем yn 1. Тогда ранговый коэффициент корреляции Кендалла вычисляется по формуле

 

4

n 1

 

 

r

 

k

 

1.

 

 

k

n(n 1) i 1

i

 

Оба коэффициента по модулю меньше единицы и при больших n между значениями rc и rk наблюдается определенное соотношение rk/rc

2/3.

122

Глава 4

Пример 4.3. На конкурсе инвестиционных проектов 10 участников получили следующие оценки (по шестибальной системе) за экологичность (экологическую безопасность) и экономическую обоснованность расчетов:

Номер

1

2

3

4

5

6

7

8

9

10

участника

 

 

 

 

 

 

 

 

 

 

Оценка за

5.6

5.5

5.9

5.45

5.75

5.85

5.3

5.2

5.35

5.4

экологичность

Оценка за

5.7

5.35

5.85

5.45

5.8

5.9

5.5

5.6

5.65

5.3

экон. обосносн.

Связаны ли между собой экологичность и экономическая обоснованность расчетов?

Решение. Тесноту связи между экологичностью и экономической обоснованностью расчетов определим с помощью ранговых коэффициентов корреляции. Ранжируем участников конкурса :

Номер

3

6

5

1

2

4

10

9

7

8

участника

 

 

 

 

 

 

 

 

 

 

Ранг за

1

2

3

4

5

6

7

8

9

10

экологичность x

i

 

 

 

 

 

 

 

 

 

 

Ранг за

2

1

3

4

9

8

10

5

7

6

экон. обосносн. y

i

 

 

 

 

 

 

 

 

 

 

Вычислим ранговые коэффициенты Спирмена и Кендалла.

 

r 1

6(1 1 0 0 16 4 9 9 4 16)

0.64,

 

 

 

 

 

 

 

c

 

 

990

 

 

 

 

 

 

 

 

 

 

 

 

 

k1 8,

k2 8 , k3 7,

k4 6,

k5 1,

k6 1,

k7 0, k8 2,

k9 0,

 

 

 

r

4 33

1 0.47.

 

 

 

 

 

 

 

 

 

 

 

 

 

k

90

 

 

 

 

 

Оценим значимость полученных коэффициентов корреляции Кендалла и Спирмена.

Проверка гипотезы о значимости выборочного коэффициента ранговой корреляции Спирмена ( H0 : rc 0 ) осуществляется с использованием Т-критерия Стъюдента. Имеем

~

n 2

 

10 2

 

 

TH rc

 

0,64

 

 

= 2,36.

~2

1 (0,64)

2

 

1 rc

 

 

 

Для различных уровней значимости ( = 0,1; = 0,05; = 0,01) по таблицам квантилей Т – распределения найдем критические точки. Получим

Вероятностно-статистические модели

123

Tкр T(1 ;n 2); Tкр Т(0,95; 8) 1,860;

2

Tкр Т(0,975; 8) 2,306; Tкр Т(0,995;8) 3,355.

Ранговая корреляция по Спирмену оказывается значимой при уровнях значимости = 0,1 и = 0,05 и не значимой для = 0,01.

Проверим значимость коэффициента корреляции Кендалла.

Имеем

~

9n(n 1)

 

90(10 1)

 

ZH rк

 

0,47

 

1,89.

2(2n 5)

2(20 5)

Критические точки определим с помощью табличной функции

Лапласа

 

1 α

 

1 0,1

 

 

 

Zкр argΦ

 

;

 

Zкр argΦ

 

 

 

1,65;

2

 

 

 

 

 

 

 

2

 

 

 

 

1 0,05

 

 

1 0,01

 

Zкр argΦ

 

 

 

1,96;

Zкр argΦ

 

 

 

 

2,59.

2

 

2

 

 

 

 

 

 

 

 

 

 

 

Ранговая корреляция по Кендаллу оказывается значимой при уровне значимости = 0,1 и не значимой для = 0,05 и = 0,01.

4.7. РЕГРЕССИОННЫЙ АНАЛИЗ

Между двумя переменными может существовать функциональная связь, когда каждому значению величины Х соответствует определенное значение величины Y : Y ( X ).

Стохастическая связь состоит в том, что одна СВ реагирует на изменение другой СВ изменением своего закона распределения. Частный случай стохастической связи – статистическая связь, когда условное математическое ожидание одной величины реагирует на изменение другой.

Чтобы найти функцию условного математического ожидания необходимо знать двухмерный закон распределения:

 

 

 

 

 

 

 

 

Yx M(Y

X x)

yf( y

x)dy;

где f( y

x) f( x,y )/ f ( x).

 

 

 

 

 

 

 

 

На практике обычно по имеющимся наблюдениям пытаются получить соответствующее уравнение связи между Х и Y. Эту зависимость и определяет регрессионный анализ.

Регрессионный анализ занимается решением следующих задач. 1. Выбор формы связи между переменными, т.е. модели регрес-

сии.

2. Оценка неизвестных параметров модели.

124

Глава 4

3. Проверка соответствующих статистических гипотез о регрес-

сии.

Форма связи между переменными, т.е. вид уравнения регрессии, выбирается исследователем либо из каких-то теоретических предпосылок, либо из соображений удобства работы с этой формулой (зависимостью), либо из вида и анализа графического изображения имеющихся статистических данных, либо из совокупности возможных математических моделей, выбрав подходящую с помощью соответствующего критерия приближения к имеющимся данным, либо из других какихлибо соображений (предпочтений).

Параметры в уравнении регрессии обычно выбираются по ме-

тоду наименьших квадратов (МНК). Основной принцип этого метода заключается в том, чтобы так определить неизвестные параметры модели, чтобы сумма квадратов отклонений имеющихся данных от выбранной кривой (уравнения) регрессии была бы минимальной:

n

)2 min,

 

 

 

Z ( yi

 

xi

где

 

xi = (xi ).

y

y

i 1

 

 

 

 

Метод наименьших квадратов удобен тем, что производная от этого критерия дает линейное уравнение.

В случае системы двух нормальных случайных величин и линейной связи между ними Y = a + bX метод наименьших квадратов дает следующее решение

 

 

~ ~ ~y

~

 

 

Yx my rxy

~

( x mx ),

 

 

 

x

 

~

1

n

~

1

n

где mx

 

xi ,

my

 

yi ,

 

 

 

n i 1

 

n i 1

 

 

 

 

 

 

 

~

 

~

1

 

~

 

 

~

n

2

 

Rxy

x

 

(xi mx )

 

,

rxy

 

.

1 n

 

~ ~

 

i 1

 

 

 

 

 

 

 

 

 

 

 

x y

 

 

 

~ ~

~x

~

 

 

Аналогично,

X y mx rxy

~

( y my ).

 

 

 

 

y

 

В случае поиска уравнения регрессии в виде полинома k-й степени исходя из основного принципа МНК

n

 

n

 

Z ( yi

 

xi

)2

( yi a0 a1xi a2xi2 ... akxik

)2 min,

y

i 1

 

i 1

 

вычисляя и приравнивая частные производные критерия Z по каждому неизвестному параметру к нулю ( Z 0), получим систему уравнений

aj

Вероятностно-статистические модели

125

 

 

n

 

n

 

... ak

n

n

a0n a1 xi a2 xi2

xik

yi ,

 

 

i 1

 

i 1

i 1

i 1

 

 

.

.

 

.

.

.

.

. .

 

 

n

 

n

1

 

n

 

n

 

k

 

k

 

k 2

 

2k

a0

xi

a1 xi

 

a2 xi

... ak xi

 

i 1

 

i 1

 

 

i 1

 

i 1

n

yixik . i 1

 

Решая

эту

систему,

найдем

неизвестные

параметры

aj ,

j

0,k

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

 

Yx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m y

 

 

rxy

cos

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X

 

 

 

 

 

 

 

 

 

m x

 

 

 

 

 

 

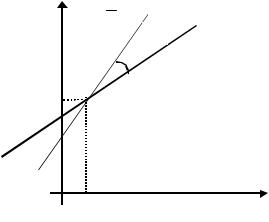
Рис.4.3. Графическое представление уравнений регрессии

 

Многомерный регрессионный анализ

 

 

B многомерном (множественном) регрессионном анализе пыта-

ются

найти

зависимость

одной переменной от

нескольких

Y ( X1,X2,...,Xm ).

 

 

 

 

 

 

 

 

 

Для линейного случая имеем уравнение множественной линей-

ной регрессии Y a0

a1X1 a2X2

... amXm . Неизвестные параметры

определяются с помощью метода наименьших квадратов.

 

 

Для

 

имеющихся

 

исходных

данных

( xij ;

yi; i

 

;

j

 

 

критерий МНК выглядит следующим об-

1,n

1,m; )

разом:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

m

 

 

 

 

 

 

 

 

 

 

 

Z ( yi (a0 ajxij ))2 min .

 

 

 

 

 

 

 

 

 

i 1

j 1

 

 

 

 

Для нахождения коэффициентов методом наименьших квадратов решаем систему, которую получаем приравниванием частных производных к нулю.

126

Глава 4

Пример 4.4. Распределение еженедельных расходов на рекламу Х и продаж Y (денежных единиц) фирмы представлены в следующей таблице:

yj

1200-1300

1300-1400

1400-1500

1500-1600

1600-1700

xi

 

 

 

 

 

40-45

1

-

-

-

-

45-50

3

2

3

-

-

50-55

2

4

4

3

-

55-60

-

4

5

6

2

60-65

-

-

3

4

2

65-70

-

-

-

-

2

Необходимо:

1)вычислить групповые средние и построить эмпирические линии регрессии;

2)предполагая, что между переменными X и Y существует линейная корреляционная зависимость: найти уравнения прямых регрессии; вычислить коэффициент корреляции; используя соответствующие линии регрессии, получить величину еженедельных продаж фирмы, если расходы на рекламу составят 80 денежных единиц.

Решение. Пусть k и m – количество интервалов группировки исходных показателей Х и Y, соответственно: k = 6, m = 5.

Вычислим групповые средние по формулам (взяв за xi и yj соответствующие середины интервалов):

 

 

 

1

 

m

 

 

 

 

 

1

 

k

 

 

y

 

 

y

n

(i = 1, , k);

x

yj

 

 

x n

(j = 1, , m),

 

 

xi n .

j 1

j ij

 

 

 

n

 

i ij

 

 

 

 

i

 

 

 

 

 

 

j i 1

 

 

 

 

 

 

m

– количество наблюдений события xi ;

где

ni nij

 

 

 

 

j 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

n j nij

– количество наблюдений события yj.

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

k

m

 

 

 

 

 

 

 

 

 

 

 

n nij 50 – общее количество наблюдений.

 

 

 

i 1j 1

 

 

 

 

 

 

 

 

 

Получим:

Вероятностно-статистические модели

 

 

 

 

 

 

127

 

 

 

x

 

1250 ;

 

 

 

 

 

 

x

 

1350 ;

 

 

 

 

 

x

1411,54 ;

 

y

 

y

 

 

 

y

1

 

 

 

 

 

 

 

 

2

3

 

 

 

 

x

 

1485,29;

 

 

 

 

 

x

 

1538,89 ;

 

 

 

 

x

1650 ;

 

y

 

 

 

y

 

 

y

 

 

 

 

4

 

 

 

 

 

 

 

5

 

6

 

 

 

y

 

48,33 ;

 

 

 

y

 

53,50;

 

 

 

y

55,17;

 

x

 

x

 

 

x

 

 

 

 

1

 

 

 

 

 

 

 

2

3

 

 

y

 

57,88;

 

 

 

y

62,50 .

 

 

 

 

 

 

 

 

x

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

Рассчитаем общие средние величины

 

 

 

 

 

 

1

k m

 

 

1 k

 

 

 

 

 

 

 

 

 

 

 

 

 

my y

 

 

yjnij

 

 

 

y

x

ni.

 

 

 

 

 

 

 

 

 

 

 

n i 1j 1

 

 

n i 1 i

 

 

 

 

1

 

k m

1

m

 

 

 

 

 

 

 

 

 

 

m

 

x

 

 

x n

 

 

x

 

n

 

 

 

n

 

 

x

 

 

 

 

 

n i 1j 1 i ij

 

j 1

yj

.j

1456;

55,6.

Уравнение прямых регрессий будем искать в виде

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

yx my rxy

( x mx );

xy mx rxy

( y my

).

 

 

 

 

x

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Величины x , y , rxy вычислим по следующим формулам

2

 

1

k m

 

2

 

 

2

1 k m

2

 

 

 

Rxy

x

 

 

 

( xi mx )

 

nij ; y

 

( yj my )

 

nij ; rxy

 

 

,

 

 

 

 

 

 

 

 

n i 1 j 1

 

 

 

 

 

n i 1 j 1

 

 

 

x y

 

 

 

 

 

 

 

 

1 k

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Rxy

 

 

( xi mx )( yj my )nij .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n i 1

j 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получим х2= 31,89; y2= 14164; Rxy = 441,4;

rxy = 0,6568 .

 

 

 

 

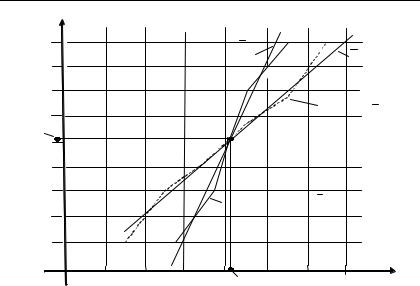
Тогда уравнения регрессий примут вид (рис.3.4)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

x 13,84x 686,42;

 

x

y 0,0312y 10,226.

 

 

 

Прогнозную величину еженедельных продаж фирмы, если расходы на рекламу составят 80 денежных единиц, определим по уравнению регрессии

y (80) = 13,84 80 + 686,42 = 1793,62 ден.ед.

128

 

 

 

 

 

Глава 4

Y

 

 

 

 

 

 

1650

 

 

 

x y

 

 

 

 

 

 

 

y x

1600

 

 

 

 

 

 

 

 

 

 

 

1550

 

 

 

 

Эмпирическая

 

 

 

 

 

1500

 

 

 

 

линия

y x i

m y

 

 

 

 

 

 

1450

 

 

 

 

 

 

1400

 

 

 

 

 

 

1350

 

 

 

Эмпирическая линия x y j

 

 

 

 

 

 

1300

 

 

 

 

 

 

1250

 

 

 

 

 

Х

 

 

 

 

55 ,6

 

 

 

 

 

 

 

40

45

50

55

m x 60

65

70

Рис.4.4. Зависимость между еженедельными расходами на рекламу

 

и объемом продаж фирмы

 

 

4.8. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ

Производственная функция – функция, устанавливающая количественную связь между результатом (эффектом) некоторого процесса и условиями его получения, по крайней мере часть из которых является управляемыми, хотя и не обязательно в рамках изучаемого процесса. Под результатом чаще всего понимается выпуск продукции (фактический или максимально возможный) некоторой производственной единицы – предприятия, отрасли, региона, народного хозяйства в целом в натуральном или денежном выражении, а под условиями – ресурсы (затраченные, использованные или наличные).

В рамках производственной функции ресурсы обычно называют факторами производства. Для отдельного предприятия или отрасли, выпускающей однородный продукт, производственные функции часто связывают объем выпуска в натуральных единицах с затратами рабочего времени по видам трудовой деятельности, различным видам сырья, энергии и т.д. (измеренными, как и выпуск, в натуральных единицах). Они отражают реально действующую технологию или спектр возможных технологий.

Производственные функции на уровне крупных отраслей, регионов или народного хозяйства в целом обычно используют агрегиро-

Вероятностно-статистические модели

129

ванные стоимостные измерители и отражают не только (и не столько) технологические, но и экономические закономерности. Концепция производственных функций базируется в первую очередь на идее замещения между факторами, т.е. на гипотезе о том, что один и тот же выпуск может быть получен при разных комбинациях используемых ресурсов. При этом речь идет о замещении как между различными ресурсами в рамках одной и той же технологии, так и между различными технологиями производства одного и того же продукта или между различными продуктами, имеющими разную ресурсоемкость.

Формально производственная функция записывается в виде:

Y F( x1, ,x2 ), где Y – объем выпуска, xi – объем i-го фактора произ-

водства.

Вид функции F и значения ее параметров определяются из теоретических представлений и имеющейся конкретной информации о моделируемом объекте.

Оценка параметров производится методами регрессионного анализа, поэтому любая оцененная производственная функция представляет собой уравнение регрессии.

Производственные функции народнохозяйственного уровня чаще всего имеют вид: Y = F(K,L) или Y = F(K,L,t), где K и L характеризуют ресурсы (затраты) основных фондов и живого труда, а t – время, вводимое для описания воздействия прочих факторов (неучтенных в K и L), среди которых главную роль играет научно-технический прогресс. Наиболее часто используются производственная функция Кобба-Дугласа, производственная функция с постоянной эластичностью замещения (CES-функция), а также производственная функция леонтьевского типа и линейная производственная функция. В теоретических работах в некоторых случаях используются производственные функции, записанные в неявном виде, иногда многофакторные.

Производственные функции позволяют рассчитать ряд характеристик, описывающих различные стороны производственного процесса. Наиболее часто используются следующие харктеристики.

1) Предельная производительность (предельный продукт) i-го

фактора – Y . Показывает, на сколько увеличится выпуск при увеличе-

xi

нии затрат i-го фактора на одну (малую) единицу и при неизменном количестве остальных факторов. Обычно предельная производительность

меньше средней: Y Y .

xi xi

130

Глава 4

2) Частная эластичность выпуска по i-му фактору (частная

факторная эластичность) – Y xi . Показывает, на сколько процентов

xi Y

увеличится выпуск при увеличении затрат i-го фактора на 1% при неизменном количестве остальных факторов. Представляет собой отношение предельной и средней производительностей.

3) Предельная норма замены (замещения) i-го фактора j-м.

Показывает количество j-го фактора, которое требуется для замены одной единицы i-го фактора при сохранении неизменного объема выпуска и неизменного количества остальных факторов. Обозначается обычно

через Rji и по определению

равна: Rji

xj

при Y const ,

xi

 

 

 

 

 

 

 

xk const,k i, j

Y

 

Y

 

 

 

 

 

 

Легко видеть, что Rji

 

/

 

 

.

 

 

x

x

 

 

 

 

i

 

 

j

 

 

4)Эластичность замены (замещения) i-го фактора j-м. Наряду

спредельной нормой замены характеризует возможности замещения одного фактора другим. В простейшем случае определяется как

 

 

 

R

ji

 

x

j

/ x

 

1

 

 

 

 

ji

 

 

 

 

 

 

 

 

i

 

при Y const, x

k

const,

k i, j .

x

 

/ x

 

R

 

 

 

 

j

 

 

ji

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

Имеются и другие определения эластичности замещения для многофакторных производственных функций. Все существующие определения эквивалентны только для двухфакторных линейно однородных производственных функций. В этом случае все они приводят к формуле

 

 

Y

 

Y

 

 

 

12 21

 

x1

x2

.

 

 

 

 

 

 

 

Y

 

2Y

 

 

 

 

 

 

 

x1 x2

Производственная функция Кобба-Дугласа – наиболее часто используемая производственная функция, которая имеет следующий вид

Y Ax1a1 xnan , где A,a1, ,an – параметры.

Частная эластичность выпуска по каждому ресурсу в рамках производственной функции Кобба-Дугласа постоянна и равна соответствующему показателю степени, а эластичность замены между любыми двумя ресурсами равна единице.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности