
Мет.моделирования и прогнозирования эк-ки
.PDF
Системы и модели массового обслуживания |
161 |
мало влияет на характеристики пропускной способности системы. Формулами Эрланга можно приближенно пользоваться и в случае,
когда СМО допускает ожидание заявки в очереди, но когда срок ожидания мал по сравнению со средним временем обслуживания одной заявки.
5.2.2.ОДНОКАНАЛЬНАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
СОТКАЗАМИ
Из общих формул СМО с отказами при n 1 имеем следующие со-
отношения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вероятность отказа в обслуживании: P |
|
P |
|
|
; |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
отк |
|
|
1 |
|
1 |
|
|
||||||||||
относительная пропускная способность СМО: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
q P |
1 P |
|
|
|
1 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
обс |
отк |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
среднее число занятых каналов: |
N |
з |
P |
|
|
|
|
|
|
|
|
|
; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
отк |
|
1 |
|
|
|
|
||||||||||||||
абсолютная пропускная способность: A q |
|
|
|
|
|
; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
среднее время занятости канала: tзан tобс 1 ;
вероятность простоя канала: P |
|
. |
|
||
0 |
|
|
5.2.3.СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С БЕСКОНЕЧНЫМ
ЧИСЛОМ КАНАЛОВ ОБСЛУЖИВАНИЯ
Вэтом случае можно считать, что при любой интенсивности входящего потока все требования, поступающие в систему, начинают немедленно обслуживаться, поскольку в рассматриваемой системе всегда имеются незанятые каналы. В такой системе имеем бесконечное число состояний.
Стационарное решение можно получить из общих формул при
n .
Врезультате имеем:
|
|
|
|
k |
|
|
ke |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
k 0,1,2,...; |
|
. |
|
P |
lim P |
t lim |
|
k! |
; |
|||||||||
|
|
|
k! |
|
||||||||||
k |
t k |
n n |
|
k |
|
|
|
|
|
|||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|||
|
|
k! |
|
|
|
|
|
|
|
|||||
Аналогично можно получить и другие характеристики СМО с бесконечным числом приборов.
162 |
Глава 5 |
5.2.4.СХЕМА ГИБЕЛИ И РАЗМНОЖЕНИЯ
Имея в распоряжении размеченный граф состояний, можно легко записать уравнения Колмогорова для вероятностей состояний (а также записать и решить алгебраические уравнения для предельных вероятностей) пользуясь следующим простым правилом.
В левой части каждого уравнения стоит производная dPk(t ) , а dt
в правой части – столько членов, сколько стрелок связано непосредственно с данным состоянием; если стрелка ведет в данное состояние, член имеет знак плюс, если ведет из данного состояния, член имеет знак минус.
Каждый член равен плотности потока событий, переводящего систему по данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Начальные условия для интегрирования отражают состояние системы в начальный момент.
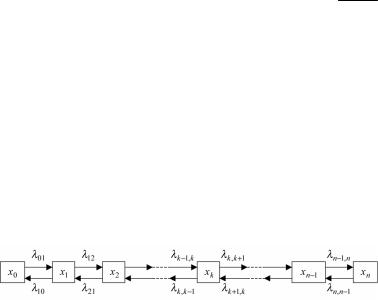
Системы массового обслуживания часто изображаются в виде состояний, вытянутых в одну цепочку. В этой цепочке каждое из сред-
них состояний x1,x2,...,xn 1 связано прямой и обратной стрелкой с каждым из соседних состояний – правым и левым, а крайние состоянияx0,xn – только с одним соседним состоянием (рис.5.5).
Рис.5.5. Схема “гибели и размножения”
Такая схема называется схемой «гибели и размножения». Этот термин возник в биологических задачах, где подобной схемой описывается изменение численности популяции. Для таких систем легко записать и решить алгебраические уравнения. Существование предельных вероятностей вытекает из того, что из каждого состояния можно перейти в каждое другое, и число состояний конечно.
Предположим, что все потоки событий, переводящие систему по стрелкам графа, – простейшие. В этом случае можно записать системы уравнений как для переходного, так и для установившегося режимов. Для переходного режима имеем системы уравнений Колмогорова:

Системы и модели массового обслуживания |
163 |
|
|
||||||||||||
|
dP0(t ) |
P (t ) |
01 |
P ; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
dt |
|
10 |
1 |
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dP1(t ) |
|
01 |
P (t ) |
21 |
P (t ) ( |
)P (t ); |
||||||||
|
|||||||||||||||
|
dt |
|
0 |
2 |
10 |
12 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP (t ) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
k |
k 1,k Pk 1(t ) k 1,k Pk 1(t ) ( k,k 1 k,k 1 )Pk (t ); k 1,n 1; |
||||||||||||
|
dt |
||||||||||||||
...
dPn(t )
n 1,nPn 1(t ) n,n 1Pn(t )
dt
Для установившегося режима имеем:
01P0 10P1; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
P |
|
P ; |
|
|
|
|
|
||||||
|
|
01 |
21 |
|
|
|
|
|
||||||||||||
|
12 |
|
10 |
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
P |
|
|
P |
; k 1,n 1; |
|||||||
|
k,k 1 |
k,k 1 |
k 1,k |
k 1,k |
||||||||||||||||
|
|
|
|
|
|
k |
|
k 1 |
|
k 1 |
|
|
||||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
P |
. |
|
|
|
|
|
|
|
|
|||
|
|
|
n 1,n |
|
|
|
|
|
|
|
|
|||||||||
|
n,n 1 |
n |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
||||||
Выражая последовательно предельные вероятности друг через друга, имеем:
01P0 10P1; |
12P1 |
21P2 |
; ... |
k 1,k Pk k,r 1Pk ; |
... n |
1,nPn 1 n,n 1Pn . |
|
Выражая все вероятности через P0 , будем иметь:
P |
01 |
P ; P |
12 |
P |
12 01 |
P ; P |
23 12 01 |
P ; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
0 |
|
2 |
|
|
21 |
|
1 |
|
|
21 |
|
0 |
3 |
|
32 |
|
21 |
|
0 |
|||||
|
10 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
10 |
|
|||||||||
P |
|
k 1,k |
... 12 01 |
P ; |
|
k |
|
. |
|
|
|
|
|
|
|
|
|||||||||||
|
1,n |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k |
|
|
|
k,k 1 |
... |
21 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В числителе полученной формулы стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данного состояния xk ), а в знаменателе – произведение всех интенсив-
ностей, стоящих у стрелок, ведущих справа налево (с начала и до xk ).
Вероятность P0 можно получить из нормировочного уравнения
n
Pi 1.
i0
164 |
|
|
|
|
|
|
|
|
Глава 5 |
|
Подставляя полученные вероятности и выражая P0 , имеем: |
||||||||||
|
01 |
|
12 01 |
|
n 1,n... 12 01 |
1 |
||||
P 1 |
|
... |
. |
|||||||
|
|
|
||||||||
0 |
|
|
|
|
|
|
... |
|
|
|
|
|
|
n,n 1 |
|
||||||
10 |
21 10 |
|
|
|
|
|||||
|
|
|
|
21 10 |
||||||
С помощью полученных соотношений удобно сразу получать вероятности состояний систем, описываемых схемой гибели и размножения, в установившемся режиме.
Пример 5.2. Рыбколхоз вылавливает в сутки в среднем 20 тонн рыбы. Улов – случайная величина, распределенная по пуассоновскому закону. Часть рыбы перерабатывается на месте. Здесь имеется два цеха производительностью каждого 4 тонны в сутки. Остальной улов перевозится на консервный завод. При цехах имеется холодильник на четыре тонны, где она может храниться не более суток, а затем ее везут на копчение. Сколько в среднем надо автомашин для перевозки рыбы, если грузоподъемность каждой 2,8 тонны и машина в сутки может сделать на завод два рейса, до пункта копчения – один рейс.
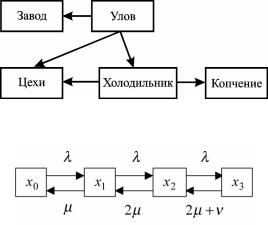
Решение. Имеем следующую схему работы СМО.
Систему можно рассматривать как СМО с отказами, если считать отказ-отвоз рыбы на завод. В этом случае граф состояний системы имеет следующую структуру:
Здесь указаны следующие состояния системы:
x0 – рыбы нет; x1 – работает 1 цех; x2 – работает 2 цеха; x3 – работают 2 цеха и холодильник.
Имеем характеристики системы 20; |
4; |
4; |
|
|
5. |
|
|||||
|
|
|
|
|
|
Тогда вероятности состояний системы определяются следующим образом:
Системы и модели массового обслуживания |
|
|
|
|
|
|
|
|
|
|
|
165 |
|||||||||||||
|
|
n |
k 1 |
|
|
|
|
25 |
|
125 |
1 |
|
|
6 |
|
|
|
|
|
|
|
||||
|
P0 |
|
|
1 5 |
|
|
|
|
|
|
|
|
|
|
0,025; |
|
|
|
|||||||
|
2 |
6 |
|
|
|
|
|
|
|
||||||||||||||||
|
k 0 |
k! |
|
|
|
|
|
|
236 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P P 0,125; |
P |
|
2 |
|
P |
0,312; |
P |
|
|
3 |
P |
0,52. |
||||||||||||
1 |
|
0 |
|
|
2 |
2! |
|
0 |
|
|
|
|
|
3 |
|
|
2 2 2 |
|
0 |
|
|||||
|
Определим среднее количество работающих цехов. |
|
|
|
|||||||||||||||||||||
|
Имеем распределение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Цеха |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|||||
|
Pi |
|
|
P0 |
|
|
|
|
P1 |
|
|
|
|
|
|
P2 |
|
|
|
P3 |
|||||
|
Тогда N3 0,125 2 0,312 2 0,52 0,125 0,624 1,04 1,79. |
||||||||||||||||||||||||
В среднем |
цеха переработают |
за |
сутки |
|
1,79 4 7,16т |
(т.е. |
|||||||||||||||||||
|
A N3 7,16т ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Остальная рыба увозится: 20 7,16 12,84 т . |
|
|
|
|
|
|||||||||||||||||||
|
На завод увозится 20 т/сутки Pотк , где Pотк Pз 0.52. |
|
|
||||||||||||||||||||||
То есть, завод перерабатывает 20 0,52 = 10,4 т/сутки, а на копчение ежесуточно отправляется 12,04 – 10,4 = 2,44 т/сутки.
Следовательно, нужны три машины, из них одна будет отвозить рыбу на копчение, две другие – на завод.
Пример 5.3. На поточной линии работают 2 контролера, которые проверяют качество выпускаемой продукции. Время, затрачиваемое на проверку одного изделия, составляет примерно одну минуту. Изделия поступают с интенсивностью 2 изд./мин. Изделие не проверяется, если в момент прохождения контролеров они оба заняты проверкой других изделий. Определить вероятности состояний СМО.
Решение. Имеем СМО с отказами с характеристиками n 2, 1, 2. Система дифференциальных уравнений для этой сис-
темы имеет вид:
|
dP0 t |
2P |
t P t ; |
|
||||
|
|
|
|
|||||
|
dt |
0 |
1 |
|
||||
|
|
|
|
|||||
|
dP1 |
t |
2P t 3P t 2P t ; |
|||||
|
|
|
||||||
|
dt |
0 |
1 |
2 |
||||
|
|
|
|
|||||
|
dP |
|
|
|
|
t 2P t , |
|
|
2 |
2P |
|
||||||
|
|
|||||||
|
dt |
1 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
где Pi t – вероятность занятости в момент времени t работой i – каналов.
166 Глава 5
Из нормировочного уравнения имеем P2 t 1 P0 t P1 t . Ис-
ключив из второго уравнения системы функцию P2 t и отбросив третье уравнение, получим:
|
dP0 t |
2P t P t ; |
|||
dt |
|||||
|
0 |
1 |
|||
dP t |
5P1 t 2. |
||||
|
1 |
|
|||
dt |
|||||
|
|
|
|||
Решение этой системы имеет вид
|
P t |
1 |
|
|
2 |
e 2t |
|
|
2 |
e 5t , |
||||||||
|
|
|
|
|
|
|||||||||||||
|
0 |
|
5 |
3 |
|
|
|
|
15 |
|
||||||||
|
|
P t |
2 |
|
2 |
|
e 5t. |
|||||||||||
|
|
|
||||||||||||||||
|
1 |
|
5 |
|
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Кроме того: P t |
2 |
|
2 |
e 2t |
|
|
4 |
e 5t . |
||||||||||
|
|
|
||||||||||||||||
2 |
5 |
|
|
3 |
|
|
|
|
|
|
|
15 |
|
|
||||
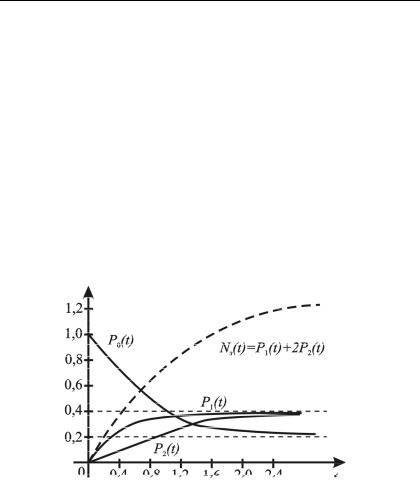
На рис.5.6. функция |
Nз t P1 t 2P2 t равна среднему числу |
|||||||||||||||||
занятых обслуживанием приборов (каналов).
Рис.5.6. Динамика изменения вероятностей состояний
Из рисунка видно, что начиная с момента времени t 2.0 , практически устанавливается стационарный режим, определяемый соотношениями:
P0 lim P0 t 0,2; |
P1 lim P1 t 0,4; |
P2 lim P2 t 0,4 . |
t 0 |
t |
t |
Пример 5.4. Клиенты, обращающиеся в мастерскую бытового обслуживания, образуют простейший поток с параметром . Каждый клиент обслуживается одним мастером в течение случайного времени с

Системы и модели массового обслуживания |
167 |
параметром . В случае отсутствия свободных мастеров клиент не
ждет, а отказывается от обслуживания. Определить, сколько надо иметь мастеров, чтобы вероятность отказа клиенту в немедленном обслуживании не превосходила 0.025, если .
Решение. Для СМО с отказами имеем зависимость вероятности
|
|
n n |
k 1 |
||
отказа от величин n, : |
Pотк |
|
|
|
. |
n! |
|
||||
|
|
k 0 |
k! |
||
|
|
|
|
|
|
При параметре 1 для различных n имеем вероятности отка-
зов:
n 2: P |
|
1 |
0,2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
отк |
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
n 3: P |
|
|
|
|
|
|
|
|
|
|
|
|
0,06; |
|
|
||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|||||||||||
отк |
|
|
|
|
16 |
|
|
|
|
|
|||||||||||
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
1 |
|
|
||||||
n 4: Pотк |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
1 |
0,015. |
||||||
|
24 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
6 |
|
|
|
65 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
||||||||
Следовательно, достаточно иметь 4 мастеров. |
|||||||||||||||||||||
5.3. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
Здесь рассмотрим системы с бесконечным (чистым) ожиданием и смешанные системы, в которых накладывают ограничения на время ожидания в очереди или в системе, на длину очереди, или смешанные ограничения на время ожидания и длину очереди.
5.3.1.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕНИЕМ НА ВРЕМЯ ОЖИДАНИЯ В ОЧЕРЕДИ
В этих системах заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания. Время ожидания ограничено некоторым сроком Tож . Если до истечения этого срока заявка не будет
принята к обслуживанию, то она покидает очередь и остается необслуженной.
Срок ожидания Tож будем считать случайным и распределен-
ным по показательному закону h t e t t 0 , где параметр – ве-
личина, обратная среднему сроку ожидания 1 .
tож
168 |
Глава 5 |
Параметр полностью аналогичен параметрам и потока
заявок и “потока освобождений”. Его можно интерпретировать как плотность “потока уходов” заявки, стоящей в очереди. Очевидно, присистема смешанного типа превращается в чистую систему с отказами; при 0 она превращается в чистую систему с ожиданием.
Заметим, что при показательном законе распределения срока ожидания пропускная способность системы не зависит от того, обслуживаются ли заявки в порядке очереди или в случайном порядке: для каждой заявки закон распределения оставшегося времени ожидания не зависит от того, сколько времени заявка уже стояла в очереди.
Благодаря допущению о пуассоновском характере всех потоков событий, приводящих к изменениям состояний системы, процесс, протекающий в ней, будет марковским. Напишем дифференциальные уравнения для вероятностей состояний системы. Возможные состояния системы:
xk k |
|
– занято ровно k |
каналов, очереди нет; |
|
0,n |
||||
xn s s 1,2,3... – заняты все n каналов, |
s заявок стоят в оче- |
|||
реди. |
|
|
||
Имеем бесконечное (хотя и |
счетное) |
множество состояний |
||
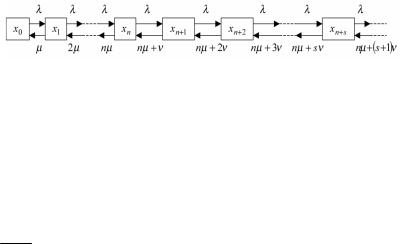
(рис.5.7). |
|
|
||
Рис.5.7. Граф переходов СМО с ограничением на время ожидания в очереди
Имеем систему бесконечного числа дифференциальных уравне-
ний:
|
dP0 t |
|
P t P t ; |
|
|
|
|
|
|||
dt |
|
|
|
|
|
||||||
|
0 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
dP1 t |
|
|
|
|
|
|
|
|
|
||
|
|
P t P t 2 P t ; ... |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
dt |
0 |
1 |
2 |
|
|
|
|
|||
|
dPk t |
|
|
|
|
|
|
|
|||
|
P |
t k P t k 1 P |
t ; |
k |
|
|
|||||
1,n 1; ... |
|||||||||||
|
|||||||||||
|
dt |
|
k 1 |
k |
k 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
dPn t Pn 1 t n Pn t n Pn 1 t ; ...
|
dPn s t |
|
P |
t n s P |
t n s 1 P |
t ;s 1,2,3,... |
|
||||||
|
dt |
n s 1 |
n s |
n s 1 |
|
|
|
|
|
|
|
||
Системы и модели массового обслуживания |
169 |
При интегрировании этой системы нужно учитывать, что хотя теоретически число возможных состояний системы бесконечно, но на практике вероятности Pn s t при возрастании sстановятся пренебре-
жимо малым, и соответствующие уравнения могут быть отброшены. Определим предельные вероятности системы в установившемся
режиме (при t ). Имеем систему алгебраических уравнений:
P0 t P1 t 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
t P t 2 P t 0; ... |
|
|
|
|
|
|
|
|
|
||||||||||||||
P |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk 1 t k Pk t k 1 Pk 1 t 0; ... |
|
|
|
|
|
||||||||||||||||||||
|
|
|
t n |
P |
|
t n |
P |
t 0; ... |
|
|
|
|
|
||||||||||||
P |
1 |
|
|
|
|
|
|
||||||||||||||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
t 0; ... |
|
|||
P |
s 1 |
t n s P |
t n s 1 P |
|
|
||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
n s |
|
|
|
|
|
|
|
n s 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь Pk |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 . |
|
|
Выразим последовательно предельные вероятности через |
|||||||||||||||||||||||
Как |
и |
в |
случае |
системы |
|
с |
отказами |
для |
любого k n имеем |
||||||||||||||||
P |
k |
|
|
P . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n 1P |
|
|
|
|
|
|
|
|
n 2P |
|
||||
Далее получаем: P |
|
|
|
|
|
|
0 |
|
; |
P |
|
|
|
|
|
|
0 |
; |
|||||||
|
|
|
|
|
n 1 |
|
|
|
n! n n |
n 2 |
|
n! n n n 2 |
|
||||||||||||
и вообще при любом s 1 имеем: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n sP |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Pn s |
|
|
|
0 |
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! n n |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
чим |
|
Подставляя в нормировочное уравнение эти зависимости полу- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
k |
|
|
|
|
|
|
n s |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
P0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
s |
|
|
|
|
|
|||||||
|
|
|
|
|
k 0 k! |
|
s 1n! n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
n j |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда

170 |
|
|
|
|
|
|
|
|
|
|
|
|
Глава 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
k |
|
|
|
|
|
n s |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P0 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
k |
|
|
s |
|
|||||||
|
k 0 k! |
|
|
s 1n! n |
n j |
||||||||
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если вместо плотностей |
и |
ввести параметры |
|||||||||||
|
|
|
|
|
tобс; |
|
|
|
tобс , |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
где , – приведенные плотности, т.е. параметры , выражают соот-
ветственно среднее число заявок и среднее число уходов заявки, стоящей в очереди, приходящиеся на среднее время обслуживания одной заявки, то вероятности состояний системы рассматриваемого типа выражаются тогда зависимостями:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
k |
n |
s |
|
|
|
|
|
|
|
|||||
|
|
|
n |
|
|
|
|
|
|
|
|||||||||
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
k 0 k! |
n! s 1 |
|
|
|
|
|
|
|
|||||||||||
|
0 |
|
|
s |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n j |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
k |
P ; k 1,n |
; |
|
|
n |
|
|
s |
||||||||
P |
P |
|
|
|
|||||||||||||||
|
|
|
|
s |
|||||||||||||||
|
k |
|
k! |
0 |
|
|
|
|
|
n s |
|
n! |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
n j |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.8)
P0 s 1.
Зная вероятности всех состояний системы, можно легко определить другие интересующие нас характеристики, в частности, вероятность Pотк того, что заявка покинет систему необслуженной.
В установившемся режиме эта вероятность есть отношение среднего числа заявок, уходящих из очереди в единицу времени, к среднему числу заявок, поступающих в единицу времени.
Вначале вычислим математическое ожидание Nоч числа заявок, находящихся в очереди:
|
|
|
|
|
|
|
|
|
s s |
|
|
|
n |
|
|
||
Nоч sPs n |
|
|
P0 |
|
. |
n! |
s |
||||
s 1 |
|
s 1 n j |
|||
|
|
|
j 1 |
|
|
|
|
|
|
||
Вероятность того, что заявка покинет систему необслуженной,
определяется формулой P |
|
|
N |
оч |
|
|
N |
оч |
. |
|
|
||||||||
отк |
|
|
|
|
|
||||
