
Мет.моделирования и прогнозирования эк-ки
.PDF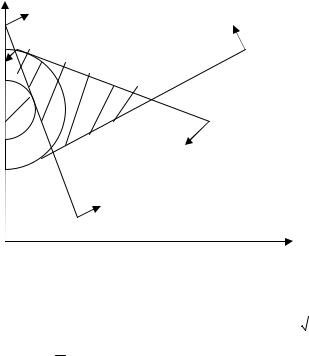
Оптимизационные модели в торговой и коммерческой деятельности |
61 |
|
X2 |
D |
|
C |
|
|
A1
A
Q
5
X2
B
X1
Рис. 2.6.
Заметим, что линия уровня поверхности
f ( x |
,x |
2 |
) x2 |
( x |
2 |
5)2 |
=C – есть окружность с радиусом |
C |
и цен- |
1 |
|
1 |
|
|
|
|
|
тром (0,5). Линия уровня определяет семейство окружностей с центром
(0,5) и радиусом 
 C . Т.к. C – произвольно, то можно найти две окружности с данным центром и касающимися области допустимых решений ВСД. Точки касания A и A1. Рассмотрим точку A1, т.к. она соответствует меньшему радиусу касания и, следовательно – меньшему значению радиуса. Линия уровня с наименьшим значением C – будет окружность, касающаяся BC в точке A.
C . Т.к. C – произвольно, то можно найти две окружности с данным центром и касающимися области допустимых решений ВСД. Точки касания A и A1. Рассмотрим точку A1, т.к. она соответствует меньшему радиусу касания и, следовательно – меньшему значению радиуса. Линия уровня с наименьшим значением C – будет окружность, касающаяся BC в точке A.
Найдём координаты точки A.
|
a) |
|
|
уравнение QA: |
|
|
|
|||||
|
x xQ k( y yQ );x k( y 5). |
|
||||||||||
|
Из |
|
уравнения |
стороны |
|
BC:3x1 x2 |
15 k1 3. Тогда |
|||||
kQA |
1 |
|
|
1 |
; |
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
|
|
||||
|
Уравнение прямой QA: |
|
|
|
||||||||
|
x |
2 |
5 |
1 |
( x 0); x 3x |
2 |
15; |
|
||||
|
|
|
||||||||||
|
|
3 |
1 |
1 |
|
|
||||||
Решаем совместно систему уравнений:
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 2 |
|
|
|
|
3x1 x2 |
15, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
3x |
2 |
15; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Решение: ( x0 3;x0 |
6). |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||
|
|
Найдём |
|
fmin f (3;6) 32 (6 5)2 10; |
|||||||||||||||
|
|
Если нужно было бы найти максимум, то требуется найти коор- |
|||||||||||||||||
динаты точки A1, |
k |
|
4 |
;k |
QA |
|
1 |
|
7 |
. Уравнение прямой QA1: |
|||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
7 |
|
|
|
k1 |
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
2 |
5 |
( x 0) 4x |
2 |
20 7x . |
|
|
|
|||||||||||
|
|
|
|
||||||||||||||||
|
4 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
Точку пересечения OA1 и CD находится из решения системы: |
|||||||||||||||||
|
|
|
7x1 4x2 20 0, |
|
|
|
|
|
|
|
|||||||||
|
|
|
4x 7x |
2 |
71 0; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Решение ( x0 2,22;x0 |
8,88); |
Найдём |
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
fmax f(2,22;8,88) |
2,222 |
(8,88 5)2 4,928 15,05 19,98 20. |
|||||||||||||||
Итак найдены экстремальные значения целевой функции:
fmin 10; fmax 20.
Метод множителей Лагранжа для решения задач нелинейного программирования
Графические методы решения задач нелинейного программирования пригодны только, когда число переменных в задаче не более двух ( x1,x2 ). Уже в трёхмерной задаче теряется наглядность и появляются
значительные вычислительные трудности. В то же время большинство экономических оптимизационных задач имеет большое число неизвестных переменных. Поэтому здесь применяются аналитические методы. Одним из самых распространённых методов является метод множителей Лагранжа, основанный на понятии условного экстремума функции нескольких переменных.
Существо метода заключается в следующем:
1.Из целевой функции Z f( x1,x2...)и системы нелиней-
ных ограничений (2.23.) формируется |
функция Лагранжа: |
|
n |
i |
|
L f ( x1,x2...) i(gi(x1,x2...) bi ) , где |
неизвестные множители |
|
i 1 |
|
|
Лагранжа.
2. Функция Лагранжа исследуется на условный экстремум, для чего используются необходимые и достаточные условия его существования:

Оптимизационные модели в торговой и коммерческой деятельности |
63 |
||||||||||||||
a) |
|
|
Необходимые условия – равенство нулю частных про- |
||||||||||||
изводных по xi |
и j: |
|
|
|
|
|
|
|
|||||||
|
L |
|
|
0, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
xi |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
i=1,2…n; j=1,2…m. |
|
|||||||
|
|
L |
|
|
|
|
|
|
|
||||||
|
|
|
|
0; |
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
|
|
|||||||
|
j |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
f |
|
|
|
|
|
m |
|
|
g j |
|
|
|
|||
|
|
|
|
|
|
|
j |
|
|
0, |
|
||||
|
|
|
|
|
xi |
|
(2.25.) |
||||||||
Т.е. xi |
|
|
|
|
j 1 |
|
|
|
|||||||
g |
j |
( x |
,x |
2 |
...) b |
j |
; |
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
||||||
Система (2.25.) содержит n+m уравнений с n+m неизвестными. Обычно эти уравнения нелинейны и точное решение их невозможно. Поэтому ограничиваются приближённым решением (с помощью численных методов и соответствующих программ на ПК).
В качестве примера рассмотрим простой случай, когда система уравнений (2.25.) имеет точное решение.
Пример 2:
Обработка статистических данных показала, что производственная функция, связывающая выпуск готовой продукции с численностью рабочих x1 и производственными фондами x2 имеет вид Z 3x1x2 . Об-
щие затраты предприятия на заработную плату и оборудование определяются соотношением 2x1 x2 60.
Нужно определить затраты предприятия на покупку оборудования и на заработную плату, при которых выпуск продукции будет максимальным:
Решение:
Составим функцию Лагранжа:
F( x1,x2, ) 3x1x2 (2x1 x2 60).
Из необходимых условий существования экстремума имеем:
F |
|
3x2 |
2 0, |
|
|
|
|
||
x |
||||
|
1 |
|
|
|
F |
|
3x1 |
0, |
|
|
|
|
||
x2 |
|
|||
|
|
|
|
|
F
2x1 x2 60 0;
64 |
|
|
|
|
|
|
|
|
|
|
|
|
Глава 2 |
Отсюда, x |
|
|
;x |
2 |
|
2 |
и тогда |
||||||
|
|
||||||||||||
|
|
1 |
3 |
|
3 |
|
|
|
|||||
|
2 |
|
2 |
60; 45;x 15;x |
2 |
30. |
|||||||
|
|
||||||||||||
3 |
3 |
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Убедимся, что в точке M(15,30) функция F достигает max (Здесь мы имеем функцию 3-х переменных: x1,x2, ). Составим полное прира-
щение функции F:
F F( x1 x,x2 x2, ) F( x1,x2, ) 3( x1 x1 )( x2 x2 )( )(2x1 2 x1 x2 x2 60) 3x1x2 (2x1 x2 60);
Так как 2x1 x2 60 0,то
F 3(x1 x1 )( x2 x2 ) ( )(2 x1 x2 ) 3x1x2 ;F 3( x1x2 x1 x2 x1 x2 ) ( )(2 x1 x2 );
Поставим в F значения x1 15;x2 30; 45;
F 3(30 x1 15 x2 x1 x2 ) ( 45 )(2 x1 x2 );
По условию 2 x1 x2 0 тогда x2 2 x1;
F 3(30 x1 15 2 x1 x1 x2 ) 3 x12 x2 6( x1 )2 0.
Следовательно F имеет максимум в точке M(15,30).
Метод множителей Лагранжа можно применять и в том случае, когда условия связи (2.24.) представляют собой неравенства. Так, если требуется найти экстремум функции Z=f(x) при условии g( x1,x2...) bi ,
то сначала |
надо найти точки |
безусловного экстремума функции |
||
Z f( x ,x |
2 |
...) из уравнений |
F |
0, затем среди этих точек отобрать |
|
||||
1 |
|
xi |
|
|
|
|
|
|
|
те, координаты которых удовлетворяют системе неравенств (2.24.) и определить точки, удовлетворяющие системе уравнений:
f |
|
|
g |
0, |
|
|
|
|
|
||
xj |
|
xj |
|||
|
|
|
|
||
g(x |
i |
) b ; |
|
||
|
|
|
i |
|
|
Точки, найденные в результате решения этой системы, вместе с точками, найденными на 1-м этапе, подлежат дальнейшему исследованию по знаку полного приращения f. Если в данных точках f <0, то мы имеем max целевой функции, если f >0, то в этих точках имеется минимум.
Оптимизационные модели в торговой и коммерческой деятельности |
65 |
Графическое решение задачи выпуклого программирования
Рассмотрим пример графического метода решения задач выпуклого программирования. Применяемость этого метода ограничена случаем 2-х искомых переменных x1 и x2, которые образуют оптимальный
план задачи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Постановка задачи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Требуется |
|
|
|
|
найти |
|
|
максимум |
|
|
целевой |
функции |
||||||||||
f 2x 0,2x2 3x |
2 |
0,2x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При ограничениях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2x 3x |
|
13, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x1 x2 |
10, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
0;x |
2 |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Преобразуем целевую функцию: |
|
|
|
|
|
|
|
|||||||||||||||
f 0,2( x2 |
|
10x 100) 20 0,2( x |
2 |
15x |
2 |
225) 45 |
||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0,2(x2 |
10x |
|
25) 5 0,2(x |
2 15x |
2 |
56,25) 11,25 |
|
|||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
0,2( x |
5)2 0,2( x |
2 |
7,5)2 |
16,25; |
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Построим линию уровня этой функции: |
|
|
|
|||||||||||||||||||
f( x1,x2 ) C; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0,2( x 5)2 0,2( x |
2 |
7,5)2 16,25 C; |
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x 5)2 |
( x |
2 |
7,5)2 |
16,25 C |
R2; |
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получим уравнение семейства окружностей радиусом R с цен-
тром x10 5;x20 7,5 . Это – выпуклая функция. Построение области до-
пустимых решений показывает, что это тоже выпуклая область (см. рис.). Таким образом, мы имеем задачу выпуклого программирования.
Опустим из центра окружности O1(5;7,5) перпендикуляр на прямую AB. Точка K – касания окружности и прямой AB определяет оптимальное решение задачи.
66 |
Глава 2 |
X2
2X1+X2=10
O1
A R
B
K
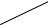 2X1+3X2=13
2X1+3X2=13
0 |
C |
X1 |
Рис. 2.7.
Найдём угловой коэффициент прямой AB: k1 2. Тогда угло- 3
вой коэффициент прямой O1K равен: k2 3 . Уравнение прямой O1K: 2
3
x2 7,5 2( x1 5).
Решая совместно уравнения:
|
|
|
3 |
|
x |
|
7,5 |
|
( x 5), |
|
2 |
|||
|
2 |
|
1 |
|
|
|
|
13; |
|
2x1 3x2 |
||||
получим координаты точки K: x1k 2;x2k 3. Максимум целе-
вой функции fmax 2 2 0,2 4 3 3 0,2 9 10,4.
В заключение отметим, что существуют другие методы решения задач выпуклого программирования – градиентные методы, и барьерных функций и др. Все эти методы реализуются на ПК.
Оптимизационные модели в торговой и коммерческой деятельности |
67 |
КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 2
1.Назовите и поясните основные классы задач и моделей математического программирования.
2.Какие приемы используются для приведения задачи линейного программирования к каноническому виду?
3.Каким образом задача максимизации может быть сведена к задаче минимизации и наоборот?
4.Приведите примеры целевой функции и ограничений модели размещения розничной торговой сети.
5.Приведите примеры целевой функции и ограничений модели планирования деятельности торгового или коммерческого предприятия.
6.Охарактеризуйте особенности постановки и решения транспортной задачи.
7.Укажите пути нахождения оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке.
8.Поясните механизм использования метода северо-западного
угла.
9.Поясните методику использования метода потенциалов.
10.В чём заключается существо метода динамического программирования?
11.Дайте определения совокупности состояний процесса и управлений этими состояниями
12.Сформулируйте принцип оптимальности Беллмана.
13.Почему расчёт по схеме динамического программирования начинается с последнего шага?
14.Дайте определение условного оптимального выигрыша и условного оптимального управления.
15.В чём заключается принципиальное различие задач нелинейного и выпуклого программирования от задачи линейного программирования?
16.Как составляется функция Лагранжа для решения задач нелинейного программирования?
17.В чём состоит существо графических методов решения нелинейных оптимизационных задач?
18.В чём состоит отличие задач нелинейного программирования от задач выпуклого программирования?
19.Дайте определение выпуклой области допустимых решений
ивыпуклой целевой функции.
68 |
Глава 2 |
ЗАДАНИЕ К ГЛАВЕ 2
Задача 1. Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Известны потребности в сырье каждого из предприятий (см. варианты задания). Сырье сосредоточено в трех местах его получения, запасы которых известны. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются соответствующей матрицей (см. варианты задания). Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
Варианты заданий Вариант 1.
Пункты |
|
Пункты назначения |
|
Запасы |
|||
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|||||
A1 |
7 |
4 |
|
17 |
|
5 |
120 |
A2 |
4 |
2 |
|
12 |
|
8 |
280 |
A3 |
3 |
8 |
|
18 |
|
2 |
160 |
Потребности |
130 |
220 |
|
60 |
|
70 |
|
|
|
Вариант 2. |
|
|
|
|
|
|
|
|
|
|
|||
Пункты |
|
Пункты назначения |
|
Запасы |
|||
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|||||
A1 |
4 |
8 |
|
4 |
|
5 |
420 |
A2 |
6 |
2 |
|
6 |
|
8 |
230 |
A3 |
3 |
11 |
|
5 |
|
12 |
560 |
Потребности |
230 |
320 |
|
160 |
|
170 |
|
|
|
Вариант 3. |
|
|
|
|
|
|
|
|
|
|
|||
Пункты |
|
Пункты назначения |
|
Запасы |
|||
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|||||
A1 |
8 |
57 |
|
35 |
|
27 |
200 |
A2 |
12 |
62 |
|
34 |
|
32 |
280 |
A3 |
11 |
68 |
|
33 |
|
11 |
320 |
Потребности |
300 |
220 |
|
130 |
|
200 |
|
|
|
Вариант 4. |
|
|
|
|
|
|
|
|
|
|
|||
Пункты |
|
Пункты назначения |
|
Запасы |
|||
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|||||
A1 |
24 |
8 |
|
34 |
|
5 |
520 |
A2 |
36 |
22 |
|
16 |
|
8 |
300 |
A3 |
43 |
11 |
|
25 |
|
12 |
600 |
Потребности |
200 |
320 |
|
400 |
|
170 |
|
Оптимизационные модели в торговой и коммерческой деятельности |
69 |
||||||||
|
|
|
Вариант 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пункты |
|
Пункты назначения |
|
|
Запасы |
|||
|
|
|
|
|
|
|
|
||
|
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
2 |
4 |
|
7 |
|
3 |
|
510 |
|
A2 |
5 |
6 |
|
8 |
|
9 |
|
90 |
|
A3 |
7 |
2 |
|
4 |
|
8 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
270 |
140 |
|
200 |
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пункты |
|
Пункты назначения |
|
|
Запасы |
|||
|
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
4 |
8 |
|
4 |
|
15 |
|
420 |
|
A2 |
6 |
22 |
|
6 |
|
17 |
|
400 |
|
A3 |
3 |
11 |
|
5 |
|
12 |
|
560 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
230 |
350 |
|
160 |
|
270 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пункты |
|
Пункты назначения |
|
|
Запасы |
|||
|
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
8 |
14 |
|
17 |
|
27 |
|
220 |
|
A2 |
12 |
16 |
|
12 |
|
32 |
|
280 |
|
A3 |
11 |
13 |
|
18 |
|
11 |
|
320 |
|
Потребности |
300 |
180 |
|
130 |
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пункты |
|
Пункты назначения |
|
|
Запасы |
|||
|
отправления |
B1 |
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
6 |
4 |
|
7 |
|
9 |
|
200 |
|
A2 |
5 |
1 |
|
8 |
|
12 |
|
270 |
|
A3 |
11 |
6 |
|
4 |
|
3 |
|
130 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
120 |
80 |
|
240 |
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
Глава 2 |
|
|
|
|
|
Вариант 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пункты |
|
|
Пункты назначения |
|
Запасы |
|||
|
отправления |
B1 |
|
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
31 |
|
7 |
|
29 |
|
5 |
120 |
|
A2 |
34 |
|
2 |
|
26 |
|
8 |
280 |
|
A3 |
43 |
|
8 |
|
17 |
|
2 |
160 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
130 |
|
220 |
|
60 |
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 10. |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
Пункты |
|
|
Пункты назначения |
|
Запасы |
|||
|
отправления |
B1 |
|
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
14 |
|
8 |
|
17 |
|
35 |
420 |
|
A2 |
16 |
|
2 |
|
12 |
|
38 |
230 |
|
A3 |
13 |
|
11 |
|
18 |
|
12 |
560 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
230 |
|
320 |
|
160 |
|
170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 11. |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
Пункты |
|
|
Пункты назначения |
|
Запасы |
|||
|
отправления |
B1 |
|
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
12 |
|
4 |
|
7 |
|
13 |
510 |
|
A2 |
5 |
|
16 |
|
8 |
|
9 |
90 |
|
A3 |
7 |
|
2 |
|
14 |
|
18 |
120 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
270 |
|
140 |
|
200 |
|
110 |
720 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 12. |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
Пункты |
|
|
Пункты назначения |
|
Запасы |
|||
|
|
|
|
|
|
|
|
||
|
отправления |
B1 |
|
B2 |
|
B3 |
|
B4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
14 |
|
8 |
|
34 |
|
15 |
500 |
|
A2 |
6 |
|
22 |
|
16 |
|
18 |
400 |
|
A3 |
13 |
|
15 |
|
25 |
|
12 |
550 |
|
|
|
|
|
|
|
|
|
|
|
Потребности |
200 |
|
390 |
|
400 |
|
170 |
|
|
|
|
|
|
|
|
|
|
|
