
Мет.моделирования и прогнозирования эк-ки
.PDF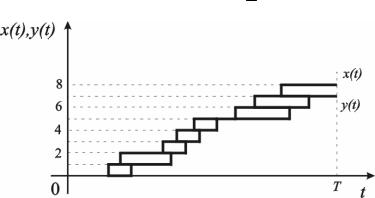
Системы и модели массового обслуживания |
151 |
очередью) и связанные с ней два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО.
Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба ее потока имеют одну и ту же интенсивность .
Обозначим:
X t – число заявок, прибывших в СМО до момента t,
Y t – число заявок, покинувших СМО до момента t.
И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов и уходов заявок соответственно (рис.5.3).
Очевидно, что для любого момента t разность Z t X t Y t есть число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z t на этом промежутке, деленному на длину интервала T :
|
1 |
T |
|
Nc |
Z t dt . |
||
T |
|||
|
0 |
||
|
|
Этот интеграл представляет собой площадь фигуры, заштрихованной на рис.5.3. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т.д.). Обозначим эти времена через t1, t2 , ...
T
Тогда Z t dt ti , где сумма распространяется на все заявки,
0 i
пришедшие за время T . Следовательно, Nc 1 ti .
T i
Рис.5.3. Динамика числа заявок в СМО

152 |
Глава 5 |
Разделим и умножим правую часть последней формулы на ин-
1
тенсивность : Nc T i ti .
Величина T есть среднее число заявок, пришедших за время T . Если разделим сумму всех времен ti на среднее число заявок, то по-
лучим среднее время пребывания заявки в системе tc .
Получаем Nc |
1 |
ti |
ti |
tc . |
Отсюда tc |
Nc |
. |
|
T |
|
|
||||||
|
i |
i T |
|
|
|
|||
Это и есть первая формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Точно таким же образом выводится вторая формула Литтла,
связывающая среднее время пребывания заявки в очереди tоч и среднее число заявок в очереди Nоч :
tоч Nоч .
Для вывода достаточно вместо нижней линии на рис.5.3 взять функцию u t – количество заявок, ушедших до момента t не из систе-
мы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет на обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время).
5.1.5.ОМАТЕМАТИЧЕСКОМ АППАРАТЕ ИССЛЕДОВАНИЯ
СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
1. При исследовании СМО часто пользуются понятием произ-
водящей функции.
Рассмотрим случайную переменную, принимающую одно из значений j 0,1, 2 ... с вероятностью Pij . Производящей функцией
данного распределения является соотношение
( z ) z jPj ,
j 0
где переменная z удовлетворяет условию 1 z 1 и не имеет опреде-
ленной |
интерпретации. |
Заметим, |
что |
1 1; 0 P0; |
||
|
d |
|
|
|
|
|
|
|
jz j 1Pj . |
|
|
|
|
|
|
|
|
|
||
|
dz |
j 0 |
|
|
|
|
Системы и модели массового обслуживания |
|
|
153 |
|
||||||
|
|
d |
|
|
|
M j . |
|
|
|
|
При z 1 имеем |
|
jP |
|
(5.1) |
||||||
|
|
|
|
|||||||
|
|
dz |
|
j |
|
|
|
|
||
|
|
j 0 |
|
|
|
|
||||
Нетрудно убедиться, |
что |
dn |
n!P при |
z 0. |
(5.2) |
|||||
|
||||||||||
|
|
|
dzn |
n |
|
|
|
|||
Таким образом, зная z , |
можно вычислить математическое |
|||||||||
ожидание рассматриваемой случайной переменной (5.1), а также, ис-
пользуя (5.2), вычислить Pj |
для любого значения |
j 0,1, 2 ... |
|
||||||||||||||||||||
|
С помощью элементарных алгебраических выкладок можно по- |
||||||||||||||||||||||
казать, |
что |
если |
Pj |
1 j |
(геометрическое |
распределение; |
|||||||||||||||||
1 0), то z |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 z |
|
|
|
|
|
|
|
|
|
je |
|
|
|
|
|||||
|
Нетрудно убедиться, что при Pj |
|
|
(пуассоновское рас- |
|||||||||||||||||||
|
|
|
|
j! |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пределение) |
будем иметь z e z ; |
при |
Pj |
Cnj p j 1 p n j |
(би- |
||||||||||||||||||
номиальное распределение; |
1 p 0) получим z 1 p pz n , а |
||||||||||||||||||||||
при Pj |
Cjj m 1p j 1 p m |
(отрицательное биномиальное распределе- |
|||||||||||||||||||||
ние; |
1 p 0) |
|
производящая |
|
функция |
будет |
иметь |
вид |
|||||||||||||||
|
1 p |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 pz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производящая функция для двух переменных имеет вид: |
|
|||||||||||||||||||||
|
|
|
|
|
|
x,y |
|
|
|
|
|
|
|
|
|
|
|
|
(5.3) |
||||
|
|
|
|
|
|
|
P xi y j |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
i 0j 0 |
|
|
|
|
|
|
|
|
|
|
|
|
Основные свойства такой производящей функции: |
|
|||||||||||||||||||||
|
1,1 |
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
||||||
|
|
P 1; |
|
|
|
|
|
|
|
P 0i0j P ; |
|
||||||||||||
|
|
|
ij |
|
|
|
|
|
|
|
|
ij |
00 |
|
|||||||||
|
|
|
i 0j 0 |
|
|
|
|
|
|
|
|
|
|
i 0j 0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
i j |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
P |
|
|
|
|
|
x,y |
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
y j |
|
|
|
|||||||||||
|
|
|
|
ij |
i! j! xi |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y 0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Наиболее часто применяется дифференциальный метод исследования СМО (составление дифференциальных уравнений Колмогорова и нахождение соответствующих вероятностей). Именно этот метод исследования СМО и применяется нами (в основном) в дальнейшем.

154 |
Глава 5 |
3. Иногда при исследовании СМО применяют преобразования
Лапласа-Стилтьеса.
Рассмотрим неотрицательную случайную переменную X и обозначим соответствующую функцию распределения через F t P X t .
Преобразованием Лапласа-Стилтьеса функции F t называ-
|
|
ется соотношение G s e stdF t , |
(5.4) |
0 |
|
где s – вещественное число, принадлежащее ограниченному интервалу в окрестности нуля, скажем, интервалу S s S .
При этом s также не имеет конкретной физической интерпре-
тации. |
|
|
|
|
|
Функцию G(s) |
|
иногда называют производящей функцией мо- |
|||
ментов, поскольку 1 n |
dnG |
|
M tn при s 0. |
||
|
dsn |
|
|||
|
|
|
|
|
t |
Рассмотрим для |
примера F t e zdz (экспоненциальное |
||||
|
|
|
0 |
||
распределение). Тогда G s |
|
|
. |
||
|
|
||||
|
|
|
|
s |
|
Если X и Y представляют собой независимые случайные переменные, то изображение по Лапласу-Стилтьесу функции распределения суммы этих переменных равняется произведению соответствующих изображений, найденных для распределений вероятностей, упомянутых случайных величин в отдельности.
Так, например, если рассмотреть зависимость
t z M 1e |
z |
||
F t |
|
|
dz (гамма-распределение), (5.5) |
M 1! |
|
||
o |
|
|
|
|
|
|
|
представляющую собой функцию распределения суммы M независимых и идентично распределенных (по экспоненциальному закону) слу-
M
чайных переменных, то G s .
s
Если же в (5.5) произвести подстановку M , то это приво-
дит к распределению Эрланга:
t |
M 1 |
e |
Mz |
|
|
F t |
M Mz |
|
dz, |
(5.6) |
|
M 1! |
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
Системы и модели массового обслуживания |
155 |
|||||||||||
для которого M t |
1 |
|
;Var t |
1 |
. |
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2M |
|
|
|||
|
|
M |
M |
|
|
s |
M |
|
||||
Тогда |
G(s) |
|
1 |
. |
|
|||||||
|
|
|
|
|
|
|||||||
|
|
M |
|
|
|
|
|
M |
|
|
||
|
|
s |
|
|
|
|
||||||
Функцию распределения при фиксированном времени обслуживания можно рассматривать как предельный случай (5.6) при M .
Вэтом случае G( s) e sM .
5.2.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ
5.2.1.МНОГОКАНАЛЬНАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
СОТКАЗАМИ
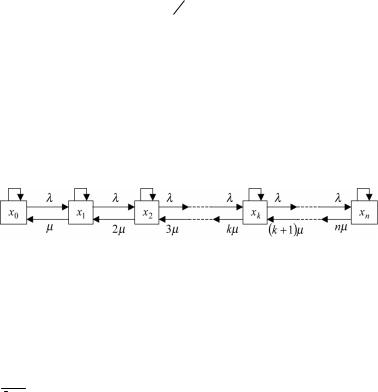
Вэтих СМО заявка, поступившая в момент, когда все каналы обслуживания были заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует. Схема возможных переходов n-канальной СМО с отказами представлена на рис.5.4.
Рис. 5.4. Схема возможных переходов n-канальной СМО с отказами Здесь xk – состояние системы, когда занято ровно k каналов (k = 0, 1, 2,
3,…, n).
Поставим задачу: определить вероятности состояний системы Pk t для любого момента времени t. Задачу будем решать при следую-
щих допущениях: поток заявок – простейший, с плотностью ; время обслуживания Tобc – показательное, с параметром
1 ; g t e t ; t 0 .
tобс
n
Очевидно, для любого момента времени Pk t 1.
k 0
Составим дифференциальные уравнения для вероятностей Pk t , начиная с P0 t . Зафиксируем момент времени t и найдем вероят-
ность P0 t t того, что в момент t t система будет находиться в

156 Глава 5
состоянии x0 (все каналы свободны). Это может произойти в двух случаях:
А – в момент t система находилась в состоянии x0 , а за время
t не перешла из него в x1 (не пришло ни одной заявки);
В – в момент t система находилась в состоянии x1, а за время
t канал освободился, и система перешла в состояние x0 . Возможностью «перескока» системы через состояние (напри-
мер, из x2 в x0 ) за малый промежуток времени можно пренебречь как величиной высшего порядка малости по сравнению с P A и P B . По теореме сложения вероятностей имеем:
|
P0 t t P A P B . |
|
Найдем |
P A по теореме умножения. |
Вероятность того, что в |
момент t система была в состоянии x0 , равна |
P0 t . Вероятность того, |
|
что за время t |
не придет ни одной заявки, равна e t 1 t . |
|
Следовательно, P A P0 t 1 t . |
|
|
Найдем |
P B . Вероятность того, что в момент времени t систе- |
|
ма была в состоянии x1 , равна P1 t . Вероятность того, что за время t
канал освободится, равна 1 e t .
С точностью до малых величин высшего порядка
1 e t t .
Следовательно, P B P1 t t .
Отсюда P0 t t P0 t 1 t P1 t t .
Перенося P t |
в левую часть, деля ее на t и переходя к пре- |
|||
0 |
|
|
|
|
делу при t 0, получим дифференциальное уравнение для P0 t : |
||||
|
|
dP0 t |
P t P t . |
|
|
|
|
||
|
|
dt |
0 |
1 |
|
|
|
|
|
Аналогичные дифференциальные уравнения могут быть составлены и для других вероятностей состояний. Возьмем любое состояние k 0 k n и найдем вероятность Pk t t того, что в момент t t
система будет в состоянии xk . Эта вероятность вычисляется как вероятность суммы уже не двух, а трех событий (по числу стрелок, направленных в состояние xk ):

Системы и модели массового обслуживания |
157 |
|
А – в момент t система была в состоянии xk |
(занято k кана- |
|
лов), а за время t не перешла из него ни в xk 1, ни в xk 1 (ни одна заявка не поступила, ни один канал не освободился);
В – в момент t система была в состоянии xk 1, а за время t
перешла в xk (пришла одна заявка);
С – в момент t система была в состоянии xk 1(занято k 1 ка-
налов), а за время t один из каналов освободился.
Найдем P A . Вычислим сначала вероятность того, что за время
t не придет ни одна заявка и не освободиться ни один из каналов:
e t e t k e k t .
Пренебрегая малыми величинами высших порядков, имеем:
k t
e 1 k t .
Отсюда P A Pk t 1 k t .
Аналогично P B Pk 1 t t; P C Pk 1 t k 1 t .
Тогда Pk t t Pk t 1 k t Pk 1 t t Pk 1 t k 1 t .
Отсюда получаем дифференциальное уравнение для
Pk t , 0 k n :
dPk t Pk 1 t k Pk t k 1 Pk 1 t .
dt
Составим уравнение для последней вероятности Pn t . Имеем
Pn t t Pn t 1 n t Pn 1 t t ,
где 1 n t – вероятность того, что за время t не освободится ни
один канал;
t – вероятность того, что за время t придет одна заявка. Получаем дифференциальное уравнение для Pn t :
dPn t Pn 1 t n Pn t . dt
Таким образом, получена система дифференциальных уравнений для вероятностей Pk t :
158 |
|
|
|
|
Глава 5 |
|
dP t |
P0 t P1 t ; |
|||||
|
0 |
|
|
|||
dt |
||||||
|
|
|
||||
dP t |
|
t k Pk t k 1 Pk 1 t ; 0 k n ; |
||||
|
k |
|
Pk 1 |
|||
dt |
||||||
|
|
|
||||
|
dPn t |
P |
t n P t . |
|||
|
||||||
|
dt |
n 1 |
n |
|||
|
|
|
||||
Эти уравнения называются дифференциальными уравнения-
ми Колмогорова. Интегрирование системы уравнений при начальных условиях P0 0 1; P1 0 ... Pn 0 0 (в начальный момент все кана-
лы свободны) дает зависимость Pk t для любого k .
Вероятности Pk t характеризуют среднюю загрузку системы и ее изменение с течением времени. В частности, Pn t есть вероятность
того, что заявка, пришедшая в момент t, застанет все каналы занятыми и получит отказ:
Pотк Pn t .
Величина q t 1 Pn t называется относительной пропуск-
ной способностью системы. Для данного момента t это есть отношение среднего числа обслуженных за единицу времени заявок к среднему числу поданных.
Система линейных дифференциальных уравнений сравнительно легко может быть проинтегрирована при любом конкретном числе каналов n .
Заметим, что при выводе дифференциальных уравнений мы нигде не пользовались допущением о том, что величины и (плотности потока
заявок и потока освобождений) постоянны. Поэтому эти уравнения остаются справедливыми и для зависящих от времени t и t , лишь бы потоки
событий, переводящих систему из состояния в состояние, оставались пуассоновскими (без этого процесс не будет марковским).
Очевидно, что сразу же после включения СМО в работу, протекающий в ней процесс еще не будет стационарным (при const, const ): в
СМО, как и в любой динамической системе, возникает переходный, нестационарный процесс. Однако спустя некоторое время этот переходный процесс затухает, и система перейдет на стационарный, установившийся режим, вероятностные характеристики которого уже не будут зависеть от времени.
Во многих задачах практики нас интересуют именно характеристики предельного установившегося режима обслуживания.
Системы и модели массового обслуживания |
159 |
Можно доказать, что для любой системы с отказами такой предельный режим существует, т.е. при t все вероятности Pk t стремятся к
постоянным пределам Pk k 0,n , а все их производные к нулю.
Чтобы найти предельные вероятности Pk (вероятности сочетаний системы в установившемся режиме), заменим в полученных выше уравнениях все вероятности Pk t их пределами Pk , а все производные положим рав-
ными нулю. Получим систему уже не дифференциальных, а алгебраических уравнений:
P0 P1 0;
Pk 1 k Pk k 1 Pk 1 0;Pn 1 n Pn 0.
k 1,n 1;
n
К этим уравнениям необходимо добавить условие: Pk 1.
1
P2 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
. |
|
|
k 0 |
|
|||||
Решим эту систему относительно Pk ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
0,n |
|
|
|
|
|
||||||||||||||||||||||||||||
Из первого уравнения имеем: |
P |
|
P . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из второго: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P P |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
P |
|
P P |
|
|
|
|
|
P . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
0 |
1 |
|
2 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
2 2 0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|||||
Аналогично, P |
|
|
P |
|
|
|
|
P |
|
|
|
|
|
2 P |
|
|
P . |
||||||||||||||||
|
|
|
|
|
|
|
2 2 |
|
|
||||||||||||||||||||||||
|
3 |
3 |
|
0 |
|
|
2 2 0 |
|
|
|
|
|
0 |
|
3! 3 0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В общем случае, для любого k n: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
P |
|
|
k |
|
P |
k |
|
P |
. |
|
|
|
|
|
(5.7) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
k |
|
|
|
k! k |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||
Здесь введено обозначение . Величина называется приве-
денной плотностью потока заявок. Это среднее число заявок, приходящееся |
|||
на среднее время обслуживания одной заявки: |
|
m . |
|
|
|||
|
tобс |
||
Формула (5.7) выражает все вероятности Pk |
через P0 . Чтобы выра- |
||
зить их непосредственно через и n , воспользуемся нормировочным усло-
n |
|
n |
k |
|
вием. Подставим в него (5.7), получим: Pk |
P0 |
|
|
1. Отсюда |
|
||||
k 0 |
|
k 0 |
k! |
|

160 |
|
|
|
|
Глава 5 |
P |
|
1 |
. |
||
|
|
||||
0 |
n |
|
k |
||
|
k 0 |
|
|
|
|
|
k! |
||||
Тогда |
P |
|
k |
|
k! |
||||
|
k |
|
n |
k |
1 |
|
|
|
|
|
|
; k 0,n . |
||
|
|||||
k 0 |
k! |
|
|
|
|
|
|
|
|
|
|
Эти формулы называются формулами Эрланга.
Формулы Эрланга справедливы при любом законе распределения времени обслуживания, лишь бы выходной поток был простейшим. Формулы Эрланга дают предельный закон распределения числа занятых каналов в зависимости от характеристик потока заявок и производительности системы обслуживания.
При k n , получаем вероятность отказа (вероятность того, что поступившая заявка найдет все каналы занятыми)
P |
P |
|
n n |
j 1 |
||
|
|
|
|
. |
||
|
|
|||||
отк |
n |
|
n! j 0 |
j! |
||
|
|
|
|
|
|
|
Зная вероятности состояний Pi , i 0,n , характеристики эффектив-
ности системы определяются соответствующими зависимости (п.5.1), в частности:
1) |
вероятность отказа в обслуживании P |
P |
|
n |
P ; |
|
|||
n! |
|
||||||||
|
|
|
|
отк |
n |
|
0 |
|
|
2) |
среднее |
число |
занятых |
каналов |
(заявок |
в |
системе) |
||
n
Nз iPi 1 Pn
i 0
A
или в другом виде: Nз 1 Pn q;
3) вероятность того, что канал в произвольный момент времени занят:
P |
|
tзап |
|
Nз |
. |
tзап tпр |
|
||||
зап |
|
|
n |
||
Несмотря на то, что формулы Эрланга в точности справедливы только при простейшем потоке заявок, ими можно с известным приближением пользоваться и в случае, когда поток заявок отличается от простейшего (например, является стационарным потоком с ограниченным последействием).
Замена произвольного стационарного потока с не очень большим последействием простейшим потоком той же плотности , как правило,
