
Мет.моделирования и прогнозирования эк-ки
.PDF
Вероятностно-статистические модели |
|
|
|
|
101 |
|
||||||
Из интегральной теоремы Муавра-Лапласа следует, что вероят- |
||||||||||||
ность того, что относительная частота |
m |
события отклоняется от его |
||||||||||
|
||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
||
вероятности в отдельном испытании P по абсолютной величине не бо- |
||||||||||||
лее, чем на , определяется по формуле: |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
m |
|
|
|
n |
|
||||||
|
|
|
|
|
|
|||||||
P |
|
n |
p |
|
2Φ |
pq |
|
. |
||||
|
|
|
|
|
|
|
|
|||||
|
|
|||||||||||
Примечание. Формула Бернулли, локальная теорема МуавраЛапласа и формула закона Пуассона дают ответ на один и тот же вопрос, а именно, они определяют вероятность того, что в n независимых испытаниях некоторое событие наступит ровно m раз, если в каждом испытании это событие может наступить с постоянной вероятностью р. По формуле Бернулли получаем точное значение вероятности этого события. Однако из-за вычислительных трудностей эта формула применяется только в случаях, когда число испытаний n невелико.
Если число испытаний будет большим, то используется локальная теорема Муавра-Лапласа, а если, кроме того, вероятность поступления события в отдельном испытании мала, то – формула Пуассона
P |
|
am |
е а; |
m 0,1, 2, ...; |
a 0. |
|
|||||
m |
|
m! |
|
|
|
Вероятность искомого события, получаемая по локальной теореме Муавра-Лапласа, оказывается достаточно точной, если число npq
не меньше 20 (npq 20). Если же npq 20 и вероятность р не мала, то
для подсчета искомой вероятности нужно обратиться к формуле Бернулли.
Формула Пуассона применяется в том случае, когда при большом числе испытаний n вероятность наступления события в каждом испытании весьма мала, а число a np невелико (не больше 10).
4.3. СИСТЕМЫ СЛУЧАЙНЫХВЕЛИЧИН
Система двух случайных величин ( X, Y ) полностью описыва-
ется двумерным законом распределения, обычно задаваемым в одной из трех форм.
1. Ряд распределения. Для системы двух дискретных случайных величин закон распределения удобно задавать в виде прямоугольной таблицы, где по одной стороне откладываются возможные значения одной переменной, по другой – значения второй переменной, а в соот-

102 Глава 4
ветствующих клетках на пересечении столбцов и строк заносятся вероятности совместного появления событий (табл.3.1).
|
|
|
|
|
|
|
Таблица 4.1 |
|
|
Ряд распределения системы двух дискретных величин |
|||||
|
|
|
|
|
|
|
|
X \Y |
y1 |
y2 |
... |
yj |
... |
yn |
|
x |
P |
P |
... |
P1j |
... |
P |
|
|
1 |
11 |
12 |
|
|
|
1n |
x |
2 |
P |
P |
... |
P2 j |
... |
P |
|
21 |
22 |
|
|
|
2n |
|
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
|
|
|
|
|
xi |
Pi1 |
Pi2 |
... |
Pij |
... |
Pin |
|
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
|
|
|
|
|
xm |
Pm1 |
Pm2 |
... |
Pmj |
... |
Pmn |
|
Здесь Pij P X xi ,Y yj ; |
|
m n |
i 1, ...,m; |
j 1, ..., n; Pij 1. |
|
|
|
i 1j 1 |
2. Функция распределения системы двух случайных величин ( X, Y ) – это вероятность совместного выполнения двух неравенств
( X x) и (Y y):
F( x,y) P( X x; Y y).
Геометрически функция F( x,y) есть вероятность попадания
случайной точки ( X, Y ) в бесконечный квадрант с вершиной в точке
( x,y), лежащий левее и ниже значения ( x,y).
Аналогично, как частный случай, функция распределения одной случайной величины F1( x) есть вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой x.
Функция F2( x) есть вероятность попадания точки в полуплос-
кость, ограниченную сверху ординатой y .
Свойства функции F( x,y):
а) F( x,y) есть неубывающая функция обоих своих аргументов,
т.е. при x2 x1 F( x2,y) F( x1,y); при y2 y1 |
F( x,y2 ) F( x,y1 ). |
|
б) |
F( x, ) F( ,y ) F( , ) 0. |
|
в) |
F( x, ) F1( x), F( ,y) F2( y), |
т.е. при одном из аргу- |
ментов, равном + , функция распределения системы превращается в
Вероятностно-статистические модели |
103 |
функцию распределения одной СВ, соответствующей другому аргументу.
г) F( , ) 1.
д) Вероятность попадания случайной точки ( X, Y ) в прямоугольник R , ограниченный абсциссами a и b и ординатами c и d, определяется через F( x,y) по соотношению
P(a Х b; c Y d) F(b, d ) F(b, c) F(a, d ) F(a, c).
3. Плотность распределения системы двух СВ представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю. Она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам:
|
|
f ( x,y ) |
lim |
P(( X ,Y ) R) |
|
|||
|
|
|
||||||
|
|
|
|
x 0 |
|
x y |
||
|
|
|
|
y 0 |
|
|
|
|
|
lim |
F( x x,y y ) F( x x,y ) F( x,y y ) F( x,y) |
|
|||||
|
|
|
||||||
|
x 0 |
x y |
||||||
|
y 0 |
|
|
|
|
|
||
|
|
|
2F( x,y) |
F ( x,y) . |
||||
|
|
|
||||||
|
|
|
x y |
|
xy |
|||
|
|
|
|
|
|
|
||
|
Элементом вероятности называется выражение f( x,y)dxdy . |
|||||||
Это вероятность попадания случайной точки ( X, Y ) в элементарный |
||||||||
прямоугольник со сторонами dx , |
dy , примыкающий к точке ( x,y). Эта |
|||||||
вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью f( x,y) и опирающегося на элементарный прямоугольник dxdy .
Вероятность попадания случайной точки в произвольную область C может быть получена суммированием (интегрированием) элементов вероятности по всей области C :
P(( X,Y ) C ) f( x,y)dxdy.
(C )
Геометрически вероятность попадания в область C изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения и опирающегося на область C . В частности, вероятность попадания случайной точки ( X, Y ) в прямоугольник R , огра-
ниченный абсциссами a и b и ординатами c и d, выражается зависимостью:

104 |
Глава 4 |
bd
P(( X ,Y ) C ) f( x,y)dxdy .
a c
Функция распределения F( x,y) выражается через функцию плотности соотношением:
|
x |
y |
F( x,y ) |
f ( x,y )dxdy . |
|
|
|
|
Основные свойства |
плотности распределения системы |
|
( X, Y ): |
|
|
1.f ( x,y) 0. |
||
|
|
|
2. |
f ( x,y)dxdy 1. |
|
Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин, входящих в систему (маргинальные законы распределения).
Ранее получили: F1( x) F( x, ); F2( y) F( ,y).
x
Так как F1( x) F( x, ) f( x,y )dxdy, то, дифференцируя
последнее выражение по x, будем иметь:
|
|
|
|
d |
|
x |
|
|
|
|
|
|
|
|
f ( x,y )dxdy |
f ( x,y )dy . |
|||
f1( x) F1( x) |
F ( x, ) |
|
|
||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Аналогично, |
f2( y ) |
|
f ( x,y )dx. |
|
|
||||
|
|
|
|
|
|
|
|
||
Зная f( x,y), легко определяются f( x) и f ( y ) . Наоборот –
труднее, так как надо знать условные законы распределения.
Условным законом распределения величины X, входящей в систему ( X, Y ), называется ее закон распределения, вычисленный при
условии, что другая случайная величина Y приняла определенное значение y. Зная закон распределения одной из величин и условный закон распределения другой, можно составить закон распределения системы.
Теорема умножения законов распределения: f( x,y ) f1(x) f ( y x).
Аналогично: f( x,y ) f2( y) f (x y).
Условные законы распределения можно определить через безусловные:
Вероятностно-статистические модели |
|
|
|
|
|
|
|
105 |
|
||||||
f( y| x) |
f( x,y) |
|
f( x,y) |
|
; |
f( x| y ) |
f ( x,y ) |
|
f ( x,y ) |
. |
|||||
|
|
|
|
|
|||||||||||
|
f( x) |
|
|
|
|
|
|
|
f ( y ) |
|
|||||
|
|
|
f (x,y )dy |
|
|
|
|
|
|
|
f( x,y )dx |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Случайная величина Y |
называется независимой от случайной |
||||||||||||||
величины X , если закон распределения величины Y не зависит от того, |
|||||||||||||||
какое значение приняла величина X . |
|
|
|
|
|
|
|
|
|
|
|||||
Для непрерывных случайных величин условие независимости |
|||||||||||||||
Y от X может быть записано в виде: |
f( y |
|
x) f ( y) при любом у. |
||||||||||||
|
|||||||||||||||
Если Y зависит от X , |
то f( y |
|
x) f ( y ). Зависимость или не- |
||||||||||||
|
|||||||||||||||
зависимость случайных величин всегда взаимны: если величина Y не зависит от X , то и величина X не зависит от Y .
Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Y называются за-
висимыми.
Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид: f( x,y) f1( x)f2( y),
т.е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.
Это условие может рассматриваться как необходимое и достаточное условие независимости случайных величин.
Числовые характеристики системы двух случайных вели- |
||
чин |
|
|
Начальным моментом порядка (k, s ) системы ( X, Y ) называ- |
||
ется математическое ожидание произведения |
Xk |
на Ys : |
k,s M[ X kYs ].
Центральным моментом порядка (k, s ) системы ( X, Y ) назы-
вается математическое ожидание произведения k -й и s-й степеней соответствующих центрированных величин:
00
k,s M[ X k Ys ] M[( X mx )k(Y my )s ].
Для дискретных случайных величин начальные и центральные моменты вычисляются, соответственно, по формулам:
m n |
m n |
k,s xik ysj Pij ; |
k,s ( xi mx )k( yj my )s Pij , |
i 1j 1 |
i 1 j 1 |
106 |
Глава 4 |
где Pij P( X xi; |
Y yj )- вероятность того, что система ( X, Y ) |
примет значения ( xi , yj ), а суммирование распространяется по всем
возможным значениям случайных величин X , Y . Для непрерывных случайных величин:
|
|
|
|
|
|
|
|
|
k,s |
|
|
xk ys f ( x,y )dxdy ; |
|
|
|
|
|
|
|
|
k,s |
|
|
( x mx )k( y my )s f( x,y )dxdy , |
|||
|
|
|||||
где f( x,y)
Очевидно,
my 0,1
– плотность распределения системы ( X, Y ).
что |
mx 1,0 M[ X1Y0 ] M[ X ] ; |
M[ X 0Y1] M[Y ] . |
|
Совокупность математических ожиданий mx и my представля-
ет собой характеристику положения центра системы ( X, Y ). Геометрически это координаты средней точки на плоскости (центр тяжести), вокруг которой происходит рассеяние всех точек ( X, Y ).
Дисперсии величин Х и Y характеризуют рассеяние случайной точки в направлении осей OX и OY :
|
|
|
0 |
0 |
0 |
|
|
|
D |
2,0 |
M[ X 2 Y0 |
] M[ X 2 ] M[( X m |
x |
)2 ] D[ X ] . |
|
|
x |
|
|
|
|
||
|
|
|
0 |
0 |
0 |
|
|
|
Dy 0,2 M[ X 0 Y2 ] M[Y2 ] M[(Y my |
)2 ] D[Y ] . |
|||||
|
Особую роль как характеристики системы играет второй сме- |
||||||
шанный |
|
|
|
центральный |
|
момент |
|
|
0 |
0 |
|
|
|
|
|
1,1 |
M [ X Y ] M [( X mx )( Y my )] Rxy , |
т.е. математиче- |
|||||
ское ожидание произведения центрированных величин.
Это ковариационный момент (т.е. момент связи, корреляци-
онный момент) случайных величин X , Y . Для дискретных случайных величин корреляционный момент выражается формулой:
m n
Rxy ( xi mx )( yj my )Pij ,
i 1j 1
а для непрерывных Rxy ( x mx )( y my )f (x,y )dxdy .
Вероятностно-статистические модели |
107 |
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеяния величин X и Y , еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
Корреляционный момент характеризует не только зависимость величин, но и их рассеяние. Поэтому для характеристики степени тесноты связи между величинами ( X, Y ) в чистом виде переходят от момен-
та R |
xy |
к безразмерной характеристике r |
|
Rxy |
|
|
, где σ |
x |
, σ |
y |
– сред- |
||
|
|
, |
|||||||||||
|
xy |
|
y |
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
ние квадратические отклонения величин |
X |
и |
Y . |
Эта характеристика |
|||||||||
называется коэффициентом корреляции величин X и Y . |
|
|
|
|
|||||||||
|
|
Две независимые случайные величины всегда являются некор- |
|||||||||||
релированными. Обратное верно не всегда. Равенство нулю коэффициента корреляции (корреляционного момента) есть необходимое, но недостаточное условие независимости случайных величин.
Условие независимости случайных величин – более жесткое, чем условие некоррелированности. Коэффициент корреляции характеризует степень тесноты только линейной зависимости между случайными величинами.
Свойства коэффициента корреляции:
rxy r( X ,Y ) r(aX b, cY d ), где a, b, c, d – константы;
1 rxy 1.
Минимальное число характеристик, с помощью которых может быть охарактеризована система n случайных величин
( X1, X2, ..., Xn ), сводится к следующему: n математических ожиданий m1, m2, ...,mn , характеризующих средние значения величин; n диспер-
сий D1, D2, ..., Dn , характеризующих их рассеяние; n(n 1) корреляци-
|
0 0 |
|
(i j ), |
онных моментов Rij M X i X j ; |
|||
|
|
|
|
0 |
0 |
|
|
( Xi Xi mi , |
X j X j mj ), |
характеризующих попарную корреля- |
|
цию всех величин, входящих в систему.

108 |
|
|
|
|
|
|
|
|
|
|
|
Глава 4 |
|
||
Дисперсия каждой из случайных величин |
|
Xi |
есть |
частный |
|||||||||||
случай корреляционного момента, |
|
а именно, |
корреляционный момент |
||||||||||||
величины X |
|
и той же величины X |
|
: D R |
0 |
|
|
0 |
0 |
. |
|
||||
i |
i |
M X |
2 |
M |
|
Xi |
Xi |
|
|
||||||
|
|
i |
ii |
|
i |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Все корреляционные моменты и дисперсии удобно располагать в виде симметричной по отношению к главной диагонали квадратной корреляционной матрицы случайных величин ( X1, X2, ..., Xn ):
R11 R12...R1n

 Rij
Rij 
 ... ... ... ,
... ... ... ,
Rn1 Rn2...Rnn
где Rij Rji ; |
i 1,n; |
j 1,n. |
В целях наглядности суждения именно о коррелированности случайных величин безотносительно к их рассеиванию часто пользуются
нормированной корреляционной матрицей 
 rij
rij 
 , составленной из коэф-
, составленной из коэф-
фициентов корреляции
|
|
|
|
|
|
|
1 r12 |
r13 |
... |
r1n |
|
r |
Rij |
|
|
|
|
1 |
r23 |
... |
r2n |
|
|
|
; |
|
r |
|
|
1 |
... |
r |
. |
||
|
|
||||||||||
ij |
|
|
|
ij |
|
|
|
|
3n |
|
|
|
i |
j |
|
|
|
|
|
... ... |
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
Плотность нормального распределения двух случайных величин выражается формулой:
|
|
|
1 |
|
|
|
|
1 |
|
|
x m |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||
f( x,y) f( x)f( y| x) |
|
|
|
|
|
exp |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
1 r |
2(1 r |
2 2 |
|||||||||||
|
|
|
|
|
2 ) |
|
|
||||||||
|
|
|
|
x y |
|
|
|
|
|
|
|
x |
|
|
|
|
2r( x mx )( y my ) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( y my ) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x y |
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот закон зависит от пяти параметров: |
mx , my , x, y , r . |
|||||||||||||
Параметры mx , my представляют собой математические ожи-
дания (центры рассеивания) величин X и Y ; x, y - их средние квад-
ратические отклонения; r – коэффициент корреляции величин X и Y . Если X и Y не коррелированы, то
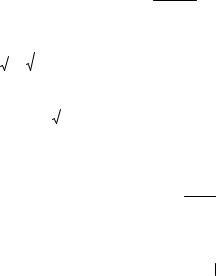
Вероятностно-статистические модели |
|
|
|
|
|
|
|
109 |
||
1 |
|
( x mx ) |
2 |
|
( y my ) |
2 |
|
|||
|
|
|
|
|
||||||
f ( x,y ) f (x )f ( y ) |
|
exp |
|
|
|
|
|
|
|
. |
2 x y |
2 |
2 |
|
2 |
2 |
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
y |
|
|
Для системы СВ, подчиненных нормальному закону, из некоррелированности величин вытекает также их независимость.
Термины "некоррелированные" и "независимые" величины для случая нормального распределения эквивалентны.
Условный закон двухмерного нормального распределения:
f( x| y ) f (x,y ) f (x)
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
exp |
|
|
|
|
|
y my r |
|
( x mx ) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 ) |
2 |
x |
|
|||||||||||||||
|
|
|
|
2 |
2(1 r |
|
||||||||||||||||||||||
|
y |
2 |
1 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
exp |
|
|
y my r |
|
|
( x mx ) |
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||
|
|
2 y|x |
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 y2|x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что последнее выражение есть плотность нормально- |
|||||||||||||||||||||||||||
го закона с центром рассеяния |
|
my|x |
my r |
y |
( x mx ) |
и средним |
||||||||||||||||||||||
|
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
квадратическим отклонением y|x y 
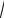 1 r2 .
1 r2 .
Из последних формул следует, что в условном законе распределения величины Y при фиксированном X x от этого значения зависит только условное математическое ожидание my x , но не дисперсия.
|
|
|
|
|
|
|
|
|
y |
( x mx ) называется линией |
||
|
Прямая my|х Yx |
yx my r |
||||||||||
|
x |
|||||||||||
регрессии |
Y |
на |
X . |
Аналогично |
прямая |
|||||||
|
||||||||||||
|
xy mx r |
x |
( y my ) есть линия регрессии X на Y . |
|||||||||
mх|y |
X |
y |
||||||||||
y |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
4.4. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ
Любое значение искомого параметра а, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайно-
сти. Такое приближенное, случайное значение ~ называют оценкой a
параметра а.
110 |
|
Глава 4 |
|
Оценка |
~ |
называется состоятельной, если с увеличением числа |
|
a |
|||
опытов n она приближается (сходится по вероятности) к искомому пара-
метру a. Если |
~ |
a , то оценка |
~ |
, удовлетворяющая такому усло- |
M a |
a |
вию, называется несмещенной.
Если выбранная нeсмещенная оценка обладает по сравнению с
другими наименьшей дисперсией, т.е. |
|
|
~ |
min, |
то она называется |
||||||||||
|
D a |
||||||||||||||
эффективной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
называется достаточной, |
если любая независимая |
|||||||||||||
Оценка a |
|||||||||||||||
оценка полученная на основе данной выборки, |
не дает какой-либо до- |
||||||||||||||
полнительной информации об оцениваемом параметре а. |
|||||||||||||||
Например, оценка дисперсии по формуле |
|
|
|
||||||||||||
|
~ |
1 n |
~ |
2 |
|
|
|
|
~ |
1 |
n |
||||
|
Dx |
|
( xi |
mx |
) , |
где |
mx |
|
xi , |
||||||
|
|
|
|||||||||||||
|
|
n i 1 |
|
|
|
|
|
|
|
|
|
n i 1 |
|||
|
|
|
|
|
~ |
|
n 1 |
|
|
|
|
|
|
||
является смещенной, так как M Dx |
|
|
|
Dx |
, поэтому лучше считать |
||||||||||
|
n |
|
|||||||||||||
|
~ |
1 |
n |
~ |
|
|
2 |
|
|
|
|
||||
дисперсию по формуле Dx |
|
(xi mx |
) |
|
. |
|
|
|
|||||||
|
|
|
|
|
|||||||||||
|
|
|
|
n 1i 1 |
|
|
|
|
|
|
|
|
|
|
|
Оценка неизвестного параметра одним числом называется
тoчечной.
Статистическая оценка, определяемая двумя числами, концами интервала, покрывающего оцениваемый параметр с некоторой вероятностью, называется интервальной.
Пусть для параметра a получена из опыта несмещенная оценка
~ . Можно оценить достоверность, надежность этой оценки, т.е. воз- a
можную ошибку при замене a на ~ . a
Назначим некоторую такую достаточно большую вероятность P (например, P = 0.9, 0.95, 0.99), что событие с вероятностью P
можно считать практически достоверным, и найдем такое значение , для которого
P( |
|
~ |
|
|
~ |
~ |
|
|
|
|
|||||
|
a a |
|
|
) P(a |
a a ) P . |
|
|
Тогда диапазон практически возможных значений ошибки, воз- |
|||||||
~ |
, будет ; большие по абсолютной вели- |
||||||
никающей при замене a на a |
|||||||
чине ошибки будут появляться только с малой вероятностью |
(1 P ) |
||||||
(рис.3.1). |
|
|
P неиз- |
||||
Последнее равенство означает, |
что с вероятностью |
||||||
вестное значение параметра a |
|
~ |
~ |
||||
попадает в интервал Ia (a ; |
a ) , |
||||||
