Мет.моделирования и прогнозирования эк-ки

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Число заявок в СМО

.PDF

Скачиваний:

Добавлен:

10.05.2015

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2718 19 20 21 22 23 24 25 26 27 > Следующая >>>

Системы и модели массового обслуживания

171

Относительная пропускная способность системы характеризуется вероятностью того, что заявка, попавшая в систему, будет обслужена

q 1 P

Nоч

оч

отк

При этом абсолютная пропускная способность A Nоч .

Зная Nз , среднее число заявок в очереди удобно вычислять по

следующей зависимости:

Nоч

Nз ,

а среднее

число

занятых

каналов можно определить по формуле Nз

n 1

kPk

n 1 Pk .

k 0

В практических расчетах бесконечные ряды, входящие в указанные выше формулы, следует заменить конечными. Эти ряды быстро сходятся, и для грубой оценки ошибки, происходящей от отбрасывания всех членов сумм, начиная с r-го, можно воспользоваться формулами:

			r


	s
	s
				e ;
	s	r!		e ;
s r	n j	r!

j 1

	s s

	s
s r	n j
	j 1


	r




		e	.
r 1!		e	.

Очевидно, что при система с ожиданием превращается в

систему с отказами: заявка мгновенно уходит из очереди. Действитель-

но, при Pn s 0 , а формулы для Pk k 0,n превращаются в формулы Эрланга для системы с отказами.

5.3.2.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

СБЕСКОНЕЧНЫМ ОЖИДАНИЕМ

Здесь заявки вообще не уходят из очереди, и поэтому Pотк 0:

каждая заявка рано или поздно дождется обслуживания. При этом в чистой системе с ожиданием не всегда имеется предельный стационарный режим при t .

Можно доказать, что такой режим существует только приn , т.е. когда среднее число заявок, приходящееся на время обслуживания одной заявки, не выходит за пределы возможностей n-канальной системы. Если же n , число заявок, стоящих в очереди, будет с течением времени неограниченно возрастать.

При n имеем предельные вероятности Pk k 0,n для чистой системы с ожиданием.

172								Глава 5
Подставляя	0 в (5.8) получаем:
n	i	n 1	1	n i	n		s 1
P0								.
P0					n!			.
i 0 i!		n! n		i 0 i!	n!	s 1ns

Так как

то	P	k
		k!
	k


	s
	s		n		;
			n
				n
n				n
s 1		1
s 1		1

n s

P0; k 1,n ; Pn s s P0 n!n

n 1	s	1 rn
r			,
r		1 r	,
s 0		1 r
s 0 .

Среднее число заявок, находящихся в очереди, определяется по формуле

n 1P

s s

Nоч

s 1 ns

n n! 1

Вероятность того, что время пребывания заявки в очереди

больше некоторой величины t

P t P

e n t ,

зп

где P

– вероятность занятости всех каналов.

зп

k n

n! 1

Среднее время ожидания tож

Pзпtобс

n 1P

Средняя длина очереди

зп

оч

n 1

n n! 1

Среднее число

свободных

от

обслуживания каналов

n 1 n k

P0 .

k 1

Среднее число занятых каналов

Nз

Среднее число заявок в системе

Nc Nоч .

Системы и модели массового обслуживания

173

5.3.3.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕНИЕМ

ПО ДЛИНЕ ОЧЕРЕДИ

В таких СМО с простейшим потоком заявок и показательным распределением времени обслуживания заявка, заставшая все каналы занятыми, становится в очередь только в том случае, если в ней находится менее m заявок. Если же число заявок в очереди равно m(больше оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.

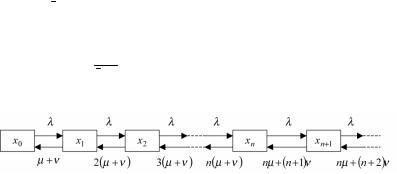
Имеем следующую схему возможных переходов:

Рис.5.8. Схема возможных переходов СМО с ограничением по длине очереди

Система (n+m+1) дифференциальных уравнений имеет вид:

dP0 t

P t P t ; ...

dPk t

Pk 1 t k Pk t k 1 Pk 1 t ; k

;

1,n 1

dPn t

t n P

t ; ...

n 1

n s

Pn s 1 t n Pn s t n Pn s 1 t ; s 1,m 1;

dPn m t

t n P

t .

n m 1

n m

При t будем иметь установившийся режим. Приравнивая все производные нулю, а все вероятности считая постоянными, получим систему алгебраических уравнений.

n m
Решая ее вместе с нормировочным уравнением Pk	1, полу-
k 0
чим предельные вероятности системы:

174

Глава 5

n k

k 0 k!


	k
P	k	P ;


k	k!	0
	k!

n	m	s 1

n!
	n
	s 1

m 1

n 1

;

n n!

k 0

		n	s
k 1,n ; P				P ; s 1,m .

		n!
	n s		n	0

Нетрудно заметить, что последние выражения получаются из формул (5.8), если положить в них 0 и ограничить суммирование по

s верхней границей m.

Вероятность отказа в обслуживании равна вероятности того, что

в очереди уже находится m заявок: P	p		n		m	P .

			n!
отк		n m		n		0

Среднее число каналов, занятых обслуживанием:

n	m			n m					A
Nз kPk n Pn k							P0			.
Nз kPk n Pn k			1	n	m	n!	P0			.
k 1	k 1			n		n!
Среднее число	каналов,	свободных						от	обслуживания:

N0 n Nз .

Среднее число заявок в очереди

m 1

n 1

1 m 1

Nоч sPn s

n n!

s 1

Складывая среднее число заявок в очереди Nоч и среднее число занятых каналов Nз , получаем среднее число заявок, связанных с системой:

Nc Nоч Nз .

Среднее время ожидания заявки в очереди tож Nоч .

Среднее время пребывания заявки в системе tc tож q .

Для одноканальной системы из общих формул нетрудно полу-

чить:

Системы и модели массового обслуживания					175
P		1		1	;
P					;
0	m 2 1			1 m 2
P		1	.
P			.
k	1 m 2
	1 m 2

Математическое ожидание числа требований в системе:

m			1					m			1
Nc kPk								k k						1 2 ... m m 1
Nc kPk		1		m 1				k k		1		m 1		1 2 ... m m 1
k 0		1						k 0		1					1 m m
	1					2			m				1		1 m m
								...									.
								...								1	.
1 m 1												1 m 1				1

	1		m		m m 1 1							m 2 m m 2
														1 1 m 2			;
	1 m 1						1 2							1 1 m 2			;

Среднее число занятых каналов Nз P1 Pk 1 P0 .

Пример 5.5. На станцию текущего ремонта автомашин поступает простейший поток заявок с интенсивностью 0,5 машины в час. Имеется одно помещение для ремонта. Во дворе станции могут одновременно находиться, ожидая в очереди, не более трех машин. Среднее время ремонта одной машины 2 часа. Для улучшения обслуживания были сделаны два предложения:

1)дополнительно построить одно помещение для ремонта;

2)дополнительно построить два помещения для ремонта. Строительство одного помещения для ремонта автомашин стоит

200 тысяч рублей. Потери от отказа в своевременном обслуживании одной машины составляют 400 руб./год. Потери от простоя одного помещения (канала) составляют 20 руб./час. Из трех возможных вариантов системы (одно, два, три помещения) необходимо выбрать лучший по критерию минимальных приведенных затрат (EH 0,2 ).

Решение. Все величины приведем к годовому периоду времени. Имеем 0,5 поступлений (заявок) в час, следовательно, за сутки их будет 24 0,5 = 12, а за год 12 365 = 4380. Имеем СМО смешанного типа с ограничением по длине очереди. Ее характеристики:

0,5; 0,5; 1; m 1; n 1.

1. Определим вероятности отказов в рассматриваемых случа-

ях:

а) n 1:

176

Глава 5

m n

n m

s 1

0,2;

отк

n m

n! n

1 1 3

б) n 2:

k 0

s 1

116

0,021;

1 1 1 2 1 4 1 8 116

отк

2 3

в) n 3:

1162

0,0022.

445

отк

3 3

1 1 1 2 1 6 1 6(1 3 1 9 1 27)

2. Определим простои системы:

а) n 1:

n k

n m

s 1

P P

0,2.

пр

n! n

k 0

s 1

Простои за год составят 8760 0,2 = 1752 ч.

б) n 2. Здесь простои помещений за год будут складываться следующим образом: Tпр (2P0 P1 )Tч.

Имеем P		16	0,34; P		P	0,34;T	365 24 8760 ч.

0	47		1	1! 0		ч

Потери за год составят 8760 (2 0,34 + 0,34) = 8760 1,02 = 8935 ч.

в) n 3. Простои за год в этом случае будут равны


	Tпр (3P0					2P1 P2 )8760 ч.
Имеем P		162	;	P			P			162		; P		2		P		81	;
0	445			1		1! 0			445			2	2!			0	445
	3 162				2 162			81			891 8760
Tпр 8760															17540.
Tпр 8760	445							445				445			17540.
	445			445				445				445

Конечные результаты расчетов сведем в табл.5.4.

Таблица 5.4

Результаты решения задачи

Кол-во	Вероят-	Простои	Количе-		Потери от	Допол-	Приве-
Кол-во	ность	Простои	Количе-	Потери от	Потери от	нитель-	Приве-
помеще-	отказа в	помеще-	ство	отказов за	простоев	ные	денные
ний для	обслу-	ний за	отказов	год, руб.	помеще-	затраты,	затраты,
ремонта	живании	год, ч.	за год		ний, руб.	руб.	руб.
1	0,20	1752	876	350400	35040	0	385440
2	0,021	8935	93	37200	178700	200000	255900
3	0,0022	17540	9,64	3856	350800	400000	434656

Вывод: целесообразно иметь два помещения для ремонта.

Системы и модели массового обслуживания

177

5.3.4.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯС ОГРАНИЧЕНИЕМ

НА ВРЕМЯ ПРЕБЫВАНИЯ ЗАЯВКИ В СИСТЕМЕ

В этом случае, если вновь прибывшая в систему заявка застанет все каналы занятыми, то она становится в очередь и ожидает обслуживания. Если время нахождения заявки в системе превысило некоторую величину tож , она покидает систему, независимо от того, принята ли

она к обслуживанию или находится в очереди. Предполагаем, что время пребывания в СМО - случайное с показательным законом распределения и параметром 1 .

tож

Имеем следующий граф состояний системы (рис.5.9).

Рис.5.9. Граф переходов с ограничением на время пребывания заявки в СМО

Система дифференциальных уравнений для вероятностей состояний:

dP0 t

P t P t ;

dP1 t

t P t 2 P

t ; ...

t k Pk t k 1 Pk 1 t ; k 1,n 1; ...

Pk 1

dPn t

t n P t n n 1 P

t ; ...

n 1

dPn s t

s 1

t n n s P

t n n s 1 P

t ;s 1;

n s

n s 1

Стационарное решение при

t определяется системой ал-

гебраических уравнений:

P0 t P1 t 0;

P t P t 2 P t 0; ...
	0		1		2
		t k P
				t k 1 P		t 0, k 1,n 1;
P				t k 1 P		t 0, k 1,n 1;
	k 1		k		k 1
		t n P		t n n 1 P			t 0; ...
P		t n P		t n n 1 P			t 0; ...
	n 1		n		n 1			t
P			t n n s P		t n n s 1 P			t
	n s 1			n s			n s 1
	n s 1			n s			n s 1

...

0;s 1.

178

Глава 5

Решение этой системы совместно с нормировочным уравнением

n m

Pk 1 дает предельные вероятности состояний.

k 0

В этом случае вероятность того, что все каналы будут свободны, определяется выражением:

							1
		n	k		s	n
		n	k		s	n
P0								,
P0			k		s	n		,
	k 0 k! 1			s 0	n n j n! 1
					j 1
					j 1

где ; .

Вероятность того, что в системе занято ровно k каналов k n , определяется зависимостью

Pk k P0 . k! 1

Вероятность того, что в очереди ровно s заявок s 1:

	n sP
Pn s		0	.
	n! 1 n	s
		n n j

j 1

Вероятность обслуживания любой заявки

n 1

n n k Pk

Pобс	k 0	.

5.3.5.СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕНИЕМ НА

ДЛИНУ ОЧЕРЕДИ И ВРЕМЯ ПРЕБЫВАНИЯ В СИСТЕМЕ

Такие системы представляют собой комбинацию из систем с ограниченным временем пребывания и систем с ограниченной длиной очереди.

Примером такой системы может служить мастерская бытового обслуживания курортного города. Отдыхающие испытывают различную потребность в ремонте фотоаппаратов, приемников, одежды и пр.

Вследствие ограниченного места хранения принятой в ремонт аппаратуры, мастерская не принимает новых заказов, если очередь на ремонт достигнет определенной величины.

Системы и модели массового обслуживания

179

С другой стороны, клиенты, как правило, ограничены временем (сроком отпуска), а поэтому по истечении срока отпуска вынуждены забирать свои вещи независимо от того, находятся ли они еще в очереди или обслуживаются.

Имеем комбинированный граф для систем с ограниченной длиной очереди и систем с ограниченным временем пребывания заявок в СМО (рис.5.10).

Рис.5.10. Комбинированный граф для систем с ограниченной длиной очереди и систем с ограниченным временем пребывания заявок в СМО

Имеем систему дифференциальных уравнений:

dP0 t

P t P t ; ...

dPk t

t k P t k 1 P

t ;

k 1,n 1; ...

k 1

dPn t

Pn 1 t

Pn t

n n 1 Pn 1 t ; ...

dPn s t

t n n s P

t n n s 1 P

t ;m s 1;

n s 1

n s

dPn m t

t n n m P

t .

n m 1

n m

Для нахождения стационарного решения этой системы при

необходимо перейти к соответствующей системе алгебраических

уравнений.

Для этих систем основные характеристики определяются сле-

дующими зависимостями.

k n

Вероятность того, что k

заявок

находится в системе:

P , где

k! 1

Вероятность того, что все каналы системы заняты, и s заявок находится в очереди 0 s m :

	n sP
Pn s		0	.
	n! 1 n	s
		n n j

j 1

180

Глава 5

Вероятность того, что в системе нет ни одной заявки, определя-

n m

ется из условия

Pk 1:

k 0

k 0 k!

n! 1

s 1

n n j

j 1

Вероятность того, что заявка будет обслужена:

						n 1
	n		n		n	n k P
	n		n			k
Pобс						k 0	.
Pобс		kPk n 1	Pk				.
	k 1		k 0

Вероятность отказа в обслуживании				Pотк 1 Pобс .

Пример 5.6. Железнодорожная касса по продаже билетов с двумя окошками представляет собой двухканальную СМО с неограниченной очередью, устанавливаемой сразу к двум окошкам (если одно окошко освобождается, ближайший в очереди пассажир его занимает). Касса продает билета в два пункта: А и B. Интенсивность потока заявок (пассажиров, желающих купить билет) для обоих пунктов А и B одинакова:A B 0,45 (пассажиров в минуту), а в сумме они образуют общий

поток заявок с интенсивностью A B 0,9 . Кассир тратит на обслу-

живание пассажира в среднем 2 минуты.

Опыт показывает, что когда у кассы образуется очередь, пассажиры жалуются на медлительность обслуживания. Поступило рационализаторское предложение: вместо одной кассы, продающей билеты и в A, и в B, создать две специализированные кассы (по одному окошку в каждый), продающие билеты одна – только в пункт А, а другая – только в пункт B. Проверить эффективность предложения расчетом.

Решение.

1. Для существующей системы имеем следующие параметры:

0,9;	0,5;		1,8;		n 2;
0,9;	0,5;		1,8;		n 2;

n	k	n 1	1
P0				0,0525;
P0				0,0525;
k 0	k!	n! n

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2718 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.20161.86 Mб570Мет. пос. по микроб.doc
#
04.05.2019107.01 Кб13Мет. ук. к семинарм 2012.doc
#
10.05.2015109.06 Кб12Мет. указ. ККР Административное право.doc
#
12.11.201995.23 Кб12мет. указ. лаб. раб. ТВиПР загот.doc
#
29.08.2019942.59 Кб22Мет.КР_ОЭиЭ_220501.doc
#
10.05.20152.61 Mб56Мет.моделирования и прогнозирования эк-ки.PDF
#
09.11.2019109.57 Кб4Мет.полож. практика Производственная.doc
#
02.11.201896.26 Кб0мет.положение Производст.doc
#
04.05.2019417.28 Кб2Мет.ук. к лаб. 2012.doc
#
10.08.2019121.86 Кб1Мет.ук. к сем.2012.doc
#
22.11.2019183.3 Кб2Мет.ук. КР.doc