
- •Экзаменационный билет № 1
- •1. Синтез механизмов по принципу Ассура. Понятие структурной группы (группы Ассура).
- •2. Определение линейных скоростей графоаналитическим методом (пример)
- •Экзаменационный билет № 2.
- •1. Понятие структурной группы (группы Ассура). Классификация структурных групп.
- •2.Определение линейных ускорений графоаналитическим методом(пример)
- •Экзаменационный билет № 3
- •1. Структурный анализ механизмов по Ассуру (пример). Формула строения механизма.
- •2..Понятие аналогов скорости и ускорения.
- •Экзаменационный билет № 4
- •2. Режимы движения машинного агрегата. Расчет кпд.
- •Экзаменационный билет № 5
- •1. Кинематический анализ механизмов. Определение линейных скоростей методом планов.
- •2..Две задачи динамики. Кинетостатика групп Ассура ( группа задается преподавателем)
- •Кинетостатика групп Ассура.
- •Экзаменационный билет № 6
- •1. Порядок силового расчета. Кинетостатика начального звена.
- •Кинетостатика начального звена
- •2. Определение закона движения начального звена.(по диаграмме Виттенбауэра)
- •Экзаменационный билет № 7
- •1. Определение линейных ускорений методом планов (пример).
- •2. Силы, действующие на звенья механизма. Определение сил инерции и моментов инерции
- •Экзаменационный билет № 8
- •2. Определение средней скорости звена приведения, коэффициента неравномерности движения
- •Экзаменационный билет № 9
- •1. Определение линейных ускорений методом планов (пример).
- •2. Динамическая модель, Требования, предъявляемые к динамической модели.
- •Экзаменационный билет № 10
- •1. Основные понятия: машина, механизм, звено, кинематическая пара, кинематическая цепь.
- •2. Определение угловых скоростей и ускорений графоаналитическим методом.
- •Экзаменационный билет № 11
- •1.Виды механизмов (примеры). Схемы механизмов.( структурная и кинематическая).
- •2. Виды балансировки роторов.
- •Экзаменационный билет № 12
- •1.Задачи динамики. Классификация сил. Последовательность силового расчета.
- •2.Приведенный момент инерции. Кпд механизма.
- •Экзаменационный билет № 13
- •1.Понятие трения. Трение на плоскости и в кинематической паре поршень- цилиндр.
- •2. Построение планов скоростей. Теорема подобия.
- •Экзаменационный билет № 14
- •1. Кинематические диаграммы. Масштабные коэффициенты.
- •2. Построение планов ускорений.
- •Экзаменационный билет № 15
- •1. Определение ускорений методом планов. (Пример).
- •2. Понятие неуравновешенности роторов, Дисбаланс. Виды балансировки.
- •Экзаменационный билет № 16
- •1. Трение в поступательной и вращательной парах.
- •2.Динамическая модель. Определение момента приведенного .
- •Экзаменационный билет № 17
- •1. Классификация кинематических пар (примеры). Кинематические цепи. Определение механизма через кц.
- •2. Для чего устанавливается маховик, Выбор маховика.
- •Экзаменационный билет № 18
- •1. Структурные формулы механизмов (плоских, пространственных). Обобщенная координата. Начальное звено.
- •2.Определение скоростей методом планов.(пример). Экзаменационный билет № 19
- •1. Кинетостатика структурной группы второго класса, второго вида.
- •2. Определение ускорений методом планов. Экзаменационный билет № 20
- •1. Виды механизмов. Схемы механизмов (структурная и кинематическая).
- •2. Исследование установившегося режима движения. Коэффициент неравномерности вращения. Экзаменационный билет № 21
- •1. Кинетостатика начального звена (пример).
- •2. Звенья и кинематические пары плоских рычажных механизмов. Экзаменационный билет № 22
- •1.Кинематический анализ механизмов Понятие аналогов скоростей и ускорений.
- •2.Установившийся режим движения механизма, Цикл движений. Уравнение движения в энергетическом виде . Экзаменационный билет № 23
- •1. Кинетостатика структурной группы второго класса первого вида.
- •2. Определение ускорений методом планов.. Экзаменационный билет № 24
- •2. Масштабные коэффициенты: планов скоростей и ускорений.
- •Экзаменационный билет № 25
- •1 . Уравнение движения механизма в дифференциальной и энергетической формах. Кпд.
- •2. Определение угловых скоростей, по плану скоростей.( значение и направление)
- •Экзаменационный билет № 26
- •1. Динамическая модель механизма. Приведенный момент инерции.
- •2. Построение плана ускорений.( Пример)
- •Экзаменационный билет № 27
- •1. Динамическая модель механизма. Приведенный момент сил.
- •2. Понятие механизма, звена, кинематической пары.
- •Экзаменационный билет № 28
- •1. Понятие структурной группы (группы Ассура). Классификация структурных групп.
- •2. Зубчатые передачи с параллельными осями колес.
- •Экзаменационный билет № 29
- •1. Динамическая модель механизма. Приведенный момент сил.
- •Экзаменационный билет № 30
- •1. Уравнение движения механизма в дифференциальной и энергетической формах. Кпд.
- •2.Классификация зубчатых передач. Передаточное отношение.
2.Определение линейных ускорений графоаналитическим методом(пример)
Полное ускорение
можно найти геометрически просуммировав
нормальное и тангенциальное ускорения,
то есть:
![]() (рис.3.4).
(рис.3.4).
Модуль вектора
нормального ускорения точки В можно
найти по формуле:
![]() .
Линия действия этого вектора будет
перпендикулярна звену АВ.
.
Линия действия этого вектора будет
перпендикулярна звену АВ.
Модуль вектора
тангенциального ускорения точки В
можно найти по формуле:
![]() .
Линия действия этого вектора будет
параллельна звену АВ.
.
Линия действия этого вектора будет
параллельна звену АВ.
П лан
ускорений механизма, как и план скоростей,
не подобен самому механизму, и является
совокупностью планов ускорений отдельных
звеньев, построенных из одного полюса
плана ускорений
лан
ускорений механизма, как и план скоростей,
не подобен самому механизму, и является
совокупностью планов ускорений отдельных
звеньев, построенных из одного полюса
плана ускорений
![]() .
.
Пример:
Заданы геометрические параметры всех звеньев и угловая скорость , которая является постоянной величиной.
Требуется определить ускорение точки М.
Решение:
Построение плана скоростей.
Скорости точек А и F равны нулю, поэтому на плане скоростей точки a и f совпадают с полюсом плана скоростей p.
М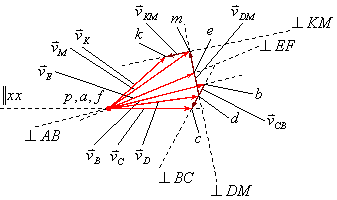 одуль
скорости точки В:
одуль
скорости точки В:
![]() .
Линия действия вектора скорости точки
В: перпендикулярно звену АВ.
.
Линия действия вектора скорости точки
В: перпендикулярно звену АВ.
Зададимся неким
масштабным коэффициентом
![]() ,
и построим вектор
,
и построим вектор
![]() на плане скоростей.
на плане скоростей.
Скорость точки С
определяется из решения векторного
уравнения
![]() ,
где
,
где
![]() - скорость точки С;
- скорость точки В,
- скорость точки С;
- скорость точки В,
![]() - скорость звена ВС в его относительном
вращении около точки В. Вектор
известен. Линия действия вектора
:
перпендикулярно звену ВС. Линия действия
вектора
:
параллельно направляющей ХХ.
- скорость звена ВС в его относительном
вращении около точки В. Вектор
известен. Линия действия вектора
:
перпендикулярно звену ВС. Линия действия
вектора
:
параллельно направляющей ХХ.
Скорость точки D
определяется с помощью теоремы подобия
и правила чтения букв. Правило чтения
букв заключается в том, что порядок
написания букв на плане скоростей или
ускорений жёсткого звена должен в
точности соответствовать порядку
написания букв на самом звене. Из
пропорции
![]() ,
можно определить длину отрезка
,
можно определить длину отрезка
![]() и, построив его на плане скоростей,
получить точку d.
Соединив полюс плана скоростей p
с точкой d
получим вектор скорости точки D
-
и, построив его на плане скоростей,
получить точку d.
Соединив полюс плана скоростей p
с точкой d
получим вектор скорости точки D
-
![]() .
.
Скорость точки
![]() определяется с помощью решения системы
геометрических уравнений:
определяется с помощью решения системы
геометрических уравнений:
![]() ,
или
,
или
![]() .
.
С корости
точек M
и K
определяются с помощью теоремы подобия
и правила чтения букв:
корости
точек M
и K
определяются с помощью теоремы подобия
и правила чтения букв:
![]() ,
следовательно,
,
следовательно,
![]() ;
;
![]() ,
следовательно,
,
следовательно,
![]() ,
при этом
,
при этом
![]() .
.
У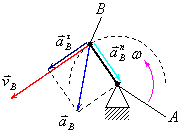 скорения
точек A
и F
равны нулю, поэтому соответствующие
им точки a
и f
на плане ускорений совпадают с полюсом
плана ускорений
(рис.3.7).
скорения
точек A
и F
равны нулю, поэтому соответствующие
им точки a
и f
на плане ускорений совпадают с полюсом
плана ускорений
(рис.3.7).
Ускорение точки
![]() можно найти с помощью решения векторного
уравнения
можно найти с помощью решения векторного
уравнения
![]() ,
где
,
где
![]() - ускорение точки
- ускорение точки
![]() ,
которое равно нулю;
,
которое равно нулю;
![]() - ускорение звена
- ускорение звена
![]() в его относительном движении около
точки
.
Ускорение звена
можно представить в виде векторной
суммы его нормального и тангенциального
ускорений, то есть:
в его относительном движении около
точки
.
Ускорение звена
можно представить в виде векторной
суммы его нормального и тангенциального
ускорений, то есть:
![]() .
Тангенциальное ускорение звена
равно нулю, поскольку его угловая
скорость не меняется, поэтому ускорение
точки
равно нормальному ускорению звена
,
то есть
.
Тангенциальное ускорение звена
равно нулю, поскольку его угловая
скорость не меняется, поэтому ускорение
точки
равно нормальному ускорению звена
,
то есть
![]() Модуль нормального ускорения звена
:
Модуль нормального ускорения звена
:
![]() .
Линия действия вектора
:
параллельно звену
.
Направление вектора
:
к точке
.
Задавшись масштабным коэффициентом
.
Линия действия вектора
:
параллельно звену
.
Направление вектора
:
к точке
.
Задавшись масштабным коэффициентом
![]() ,
строится вектор
,
строится вектор
![]() .
.
Скорость точки
![]() находится с помощью геометрического
решения векторного уравнения:
находится с помощью геометрического
решения векторного уравнения:
![]() ,
где
,
где
![]() - ускорение точки
;
- ускорение точки
;
- ускорение точки
;
- ускорение точки
;
![]() - нормальное ускорение звена
- нормальное ускорение звена
![]() ;
;
![]() - тангенциальное ускорение звена
.
Направление ускорения точки
:
параллельно направляющей
.
Ускорение точки
известно. Модуль нормального ускорения
звена
:
- тангенциальное ускорение звена
.
Направление ускорения точки
:
параллельно направляющей
.
Ускорение точки
известно. Модуль нормального ускорения
звена
:
![]() ;
линия действия вектора
:
параллельно звену
;
направление вектора
:
к точке
.
Линия действия вектора тангенциального
ускорения звена
:
перпендикулярно звену
.
;
линия действия вектора
:
параллельно звену
;
направление вектора
:
к точке
.
Линия действия вектора тангенциального
ускорения звена
:
перпендикулярно звену
.
Ускорение точки
![]() находится с помощью теоремы подобия и
правила чтения букв:
,
следовательно,
находится с помощью теоремы подобия и
правила чтения букв:
,
следовательно,
![]() .
.
Ускорение точки
можно найти с помощью решения системы
векторных уравнений:
![]() или
или
![]() .
.
Ускорения точек
![]() и
и
![]() определяются с помощью теоремы подобия
и правила чтения букв:
,
следовательно,
определяются с помощью теоремы подобия
и правила чтения букв:
,
следовательно,
![]() ;
;
![]() ,
следовательно,
,
следовательно,
![]() .
.
