
- •Глава I. Математический аппарат и основные понятия электродинамики.
- •§1.1. Постулаты специальной теории относительности.
- •§1.2. Четырехмерное пространство и четырехмерная символика.
- •§1.3. Преобразование Лоренца для координат и времени.
- •§1.4. Преобразования Лоренца для скоростей и углов.
- •§1.5. Кинематические «парадоксы» сто.
- •§1.6. Ковариантные формы преобразований Лоренца.
- •§1.7. Четырехмерные векторы.
- •§1.8. Четырехмерные тензоры.
- •§1.9. Четырехмерный вектор-потенциал и тензор напряженности электромагнитного поля.
- •§1.10. Инварианты электромагнитного поля.
- •Глава II. Релятивистская механика.
- •§2.1. Четырехмерные векторы импульса и силы.
- •§2.2. Вариационный принцип Гамильтона в релятивистской механике.
- •§2.3. Вывод силы Лоренца.
- •§2.4. Релятивистские уравнения Гамильтона.
- •§2.5. Законы сохранения и свойства симметрии четырехмерного пространства.
- •§2.6. Тензор спина и малая группа Лоренца.
- •§2.7. Четырехмерный вектор спина.
- •§2.8. Уравнение Баргмана-Мишеля-Телледи.
- •Глава III. Полевая электродинамика.
- •§3.1. I пара уравнений Максвелла в дифференциальной форме.
- •§3.2. Вариационный принцип Гамильтона в теории поля.
- •§3.3. II пара уравнений Максвелла в дифференциальной форме для "чистого" поля.
- •§3.4. II пара уравнений Максвелла при наличии зарядов и токов.
- •§3.5. I пара уравнений Максвелла в интегральной форме.
- •§3.6. II пара уравнений Максвелла в интегральной форме.
- •§3.7. Четырехмерный вектор плотности тока.
- •§3.8. Четырехмерный вектор плотности силы.
- •§3.9. Тензор плотности энергии и импульса частиц.
- •§3.10. Тензор плотности энергии-импульса электромагнитного поля.
- •§3.11. Закон сохранения плотности энергии-импульса в дифференциальной форме.
- •§3.12. Вектор Пойнтинга.
- •§3.13. Тензор натяжений Максвелла.
- •§3.13. Законы сохранения в дифференциальной форме как следствие однородности и изотропности пространства.
- •§3.16. Орбитальный и спиновый угловые моменты электромагнитного поля.
- •Глава IV. Теория частиц и полей.
- •§4.1. Об устойчивости статической системы электрических зарядов.
- •§4.2. Собственная масса замкнутой системы частиц и полей.
- •§4.3. Электромагнитная масса электрона.
§1.6. Ковариантные формы преобразований Лоренца.
Ранее были получены преобразования Лоренца для координат и времени:
![]() ,
где
,
где
![]() .
.
Эти формулы не являются ковариантными. Здесь выделены отдельные координаты и время, тогда как ковариантные формы подразумевают отсутствие выделенных координат.
![]() ,
,
![]() .
.
![]() -
матрица, которая представляет собой
коэффициенты преобразования. Эти
коэффициенты постоянны.
-
матрица, которая представляет собой
коэффициенты преобразования. Эти
коэффициенты постоянны.
 .
.
Положим
![]() :
:
![]() .
.
Сравнивая полученное выражение с известным преобразованием Лоренца, определяем соответствующие коэффициенты преобразования :
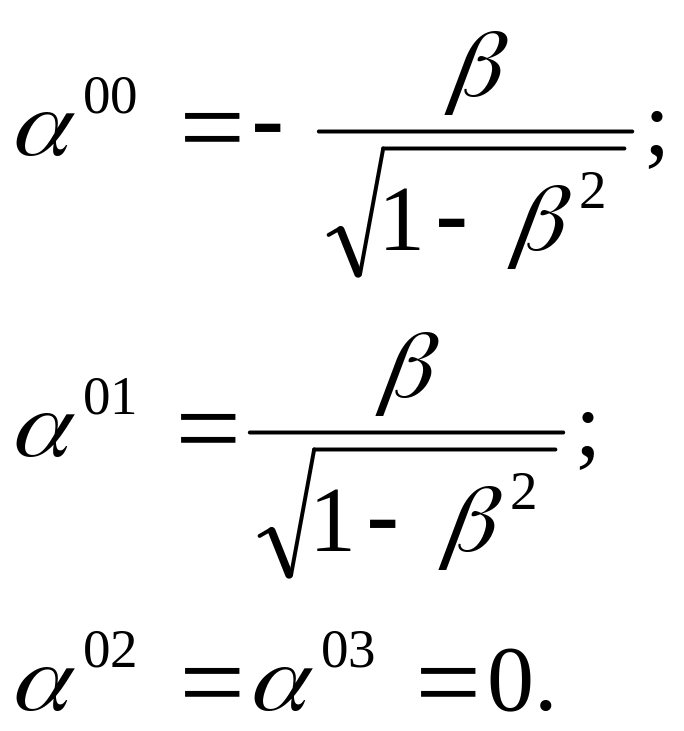
Положим теперь
![]() :
:
![]() .
.
Соответственно, находим:
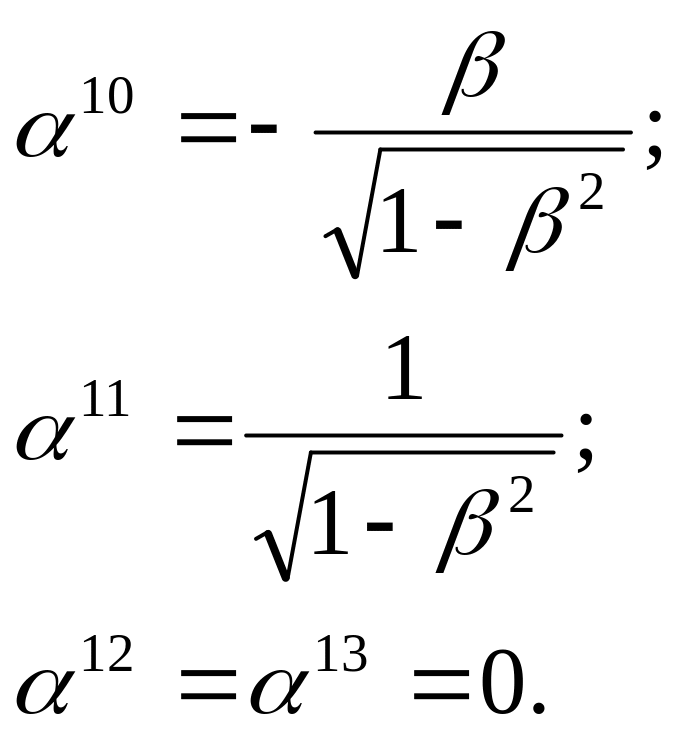
Полагая далее
![]() и
и
![]() ,
получаем, что
,
получаем, что
![]() и
и
![]() .
Все остальные коэффициенты равны нулю.
Таким образом, матрица преобразования
Лоренца для случая, когда система
движется вдоль оси
«неподвижной» системы
имеет следующий вид:
.
Все остальные коэффициенты равны нулю.
Таким образом, матрица преобразования
Лоренца для случая, когда система
движется вдоль оси
«неподвижной» системы
имеет следующий вид:
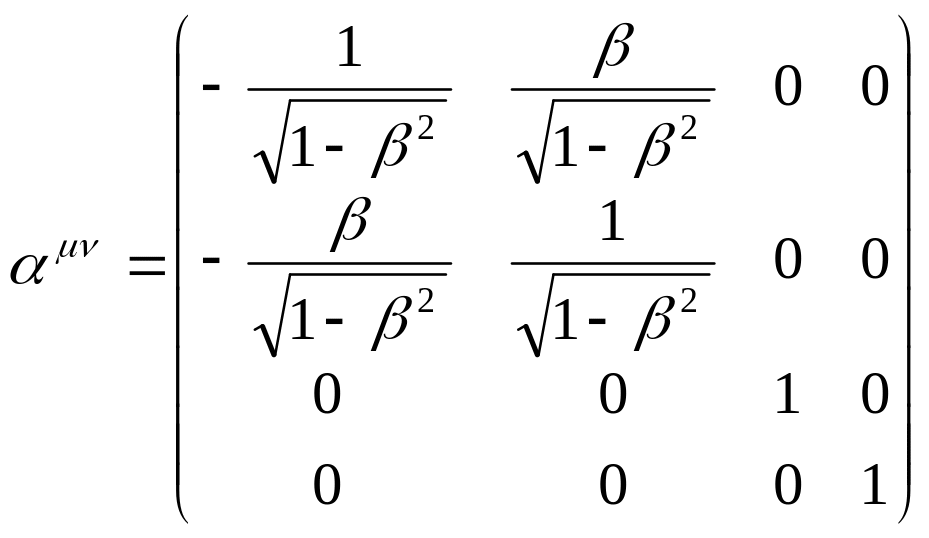 .
.
Это – матрица частного преобразования Лоренца. Перепишем ее следующим образом:
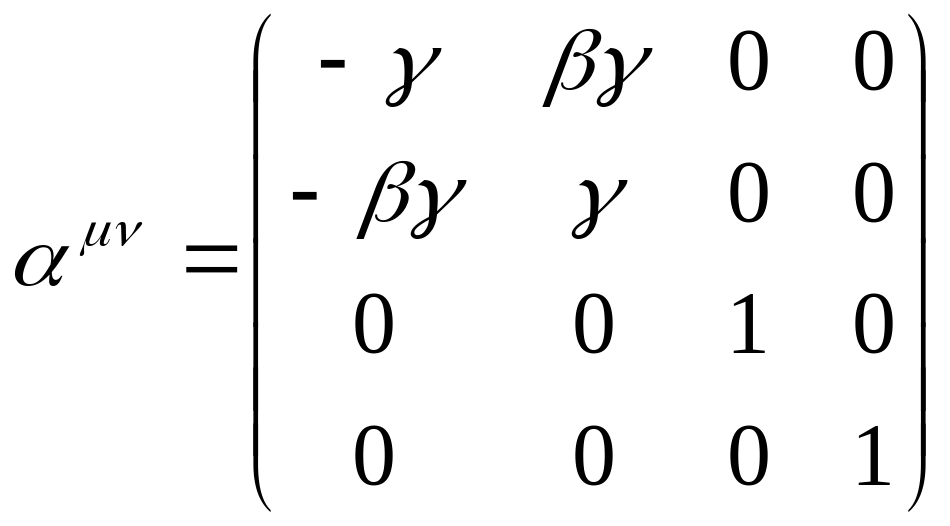 .
.
Если речь идет об обратном преобразовании
Лоренца, то вместо матрицы
следует использовать обратную матрицу
![]() :
:
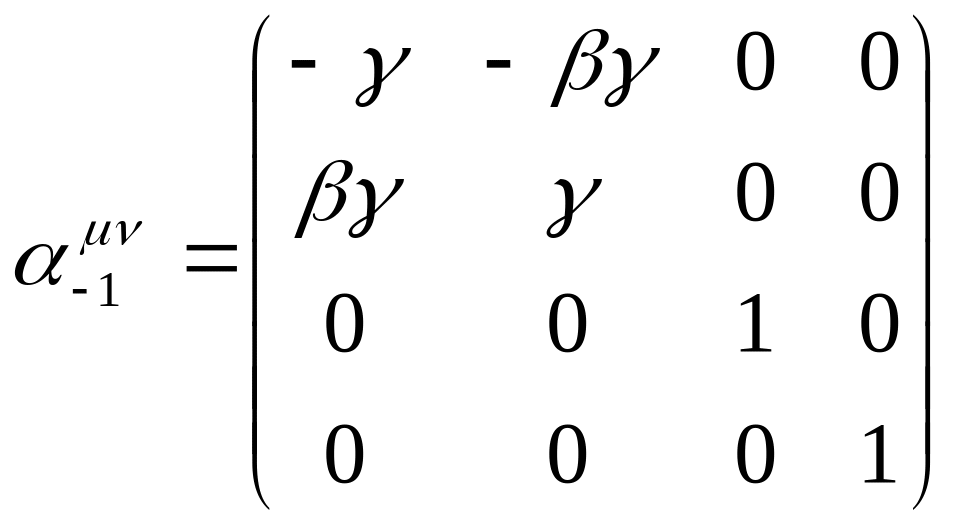 .
.
Причем справедливо следующее выражение:
![]() .
.
Очевидно, что
![]() ,
то есть
,
то есть
![]() :
:
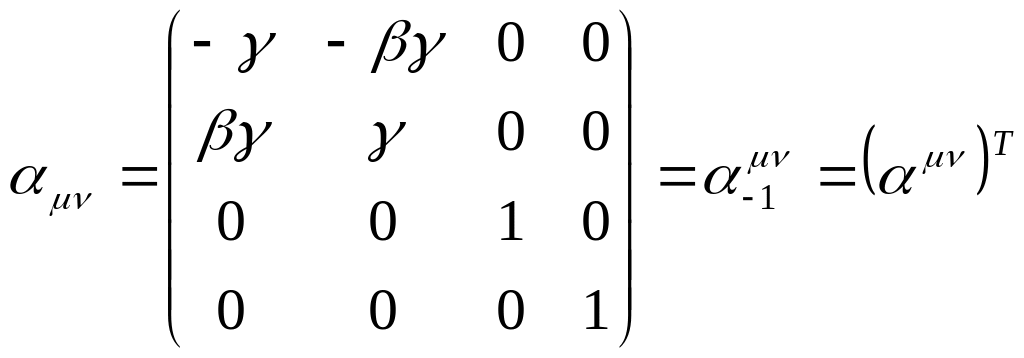 .
.
Иначе, матрица удовлетворяет следующему условию:
![]() - единичная матрица.
- единичная матрица.
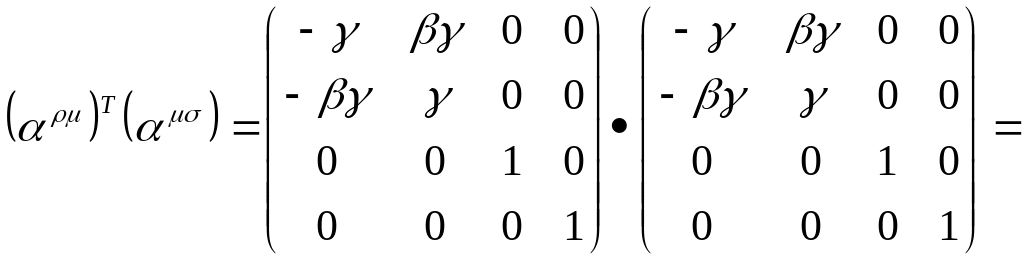
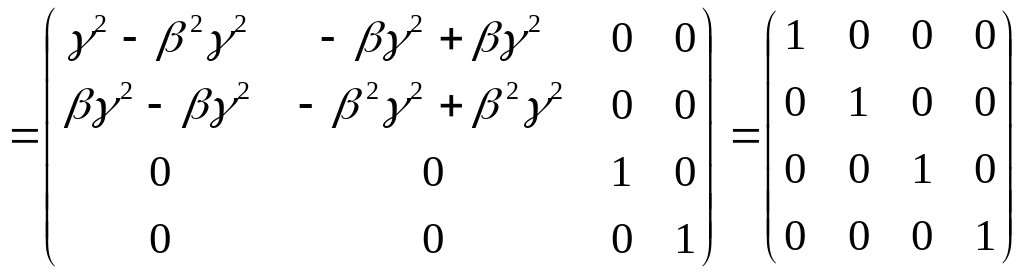 .
.
Следует убедиться в правдивости найденных
коэффициентов. Для этого должно
выполняться
![]() :
:
![]()
![]() .
.
Несложно показать, что в случае произвольного преобразования Лоренца матрица преобразования выглядит таким образом:
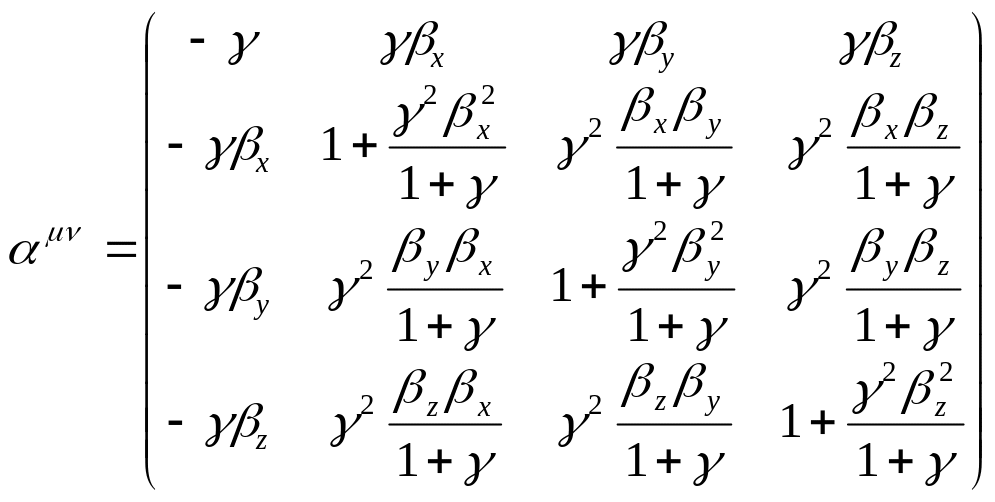 .
.
§1.7. Четырехмерные векторы.
Четырехмерные векторы – совокупность четырех величин, которые при переходе от одной инерционной системы отсчета к другой преобразуется по закону:
![]() ,
,
![]() .
.
Четырехмерный вектор скорости определяется
как
![]() ,
где
- собственное время.
,
где
- собственное время.
![]() ,
где
- обычная Ньютоновская скорость.
,
где
- обычная Ньютоновская скорость.
![]() ,
так как
,
так как
![]() .
.
Так же нетрудно показать, что
![]() :
:
![]() .
.
То есть свертка двух четырехмерных векторов есть инвариант. Найдем инвариант, соответствующий четырехмерному вектору скорости:
![]()
![]() .
.
![]() .
.
Интересно, что в состоянии покоя (при
![]() )
будем иметь:
)
будем иметь:
![]() .
.
Такие четырехмерные векторы, у которых в системе компонент имеется только временная, называется временеподобными. Другим примером четырехмерных векторов служат пространствоподобные вектора. Таковым, например, является четырехмерный вектор ускорения:
![]() - пространствоподобный вектор.
- пространствоподобный вектор.
Найдем его компоненты:
![]() .
.
Аналогично с радиус-вектором, введем производную по лабораторному времени:
![]()
![]() .
.
Вычислим
![]() :
:
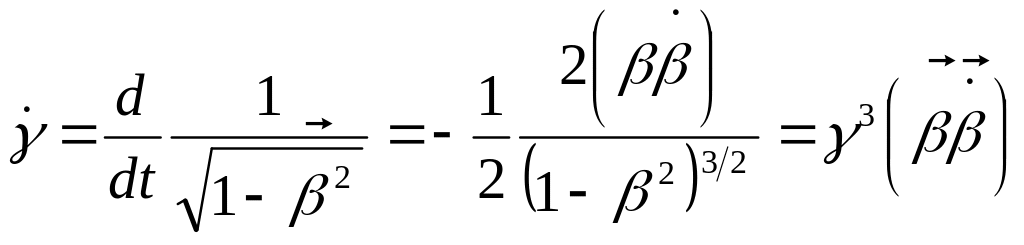 .
.
Подставим это значение
в выражение для
![]() :
:
![]() .
.
Фактически, это новый четырехмерный вектор. Перепишем это выражение, объединив 0-компоненты и пространственные компоненты:
![]() .
.
Наконец, чтобы получить выражение,
похожее на Ньютоновское ускорение
![]() .
Для этого внесем
.
Для этого внесем
![]() в квадратные скобки и получим:
в квадратные скобки и получим:
![]() =>
=>
=>![]() .
.
Убедиться в его пространствоподобности
можно, если рассмотреть
в состоянии покоя
![]() :
:
![]() =>
=>
![]() .
.
Так образом,
- пространствоподобный вектор. Можно
показать, что четырехмерные вектора
скорости
![]() и ускорения
взаимно ортогональны в четырехмерном
пространстве:
и ускорения
взаимно ортогональны в четырехмерном
пространстве:
![]() .
Покажем это:
.
Покажем это:
=>
![]() =>
=>
=> => они взаимно ортогональны.
Также можно показать, что справедливо
![]() или иначе
или иначе
![]() .
.
Стоит отметить, что введя понятие четырехмерного вектора, мы определяем преобразования Лоренца для четырехмерного вектора:
![]() .
.
Запишем преобразования Лоренца для произвольного четырехмерного вектора:
![]() .
.
Также можно доказать, что
![]() .
.
