§3.7. Четырехмерный вектор плотности тока.
Проблема состоит в том, что в рамках теории поля понятия точечного заряда или заряженной частицы не существует. В ней все физические величины в некотором смысле рассредоточены в пространстве. Но так как объективно понятие точечного заряда существует, необходимо разработать специальный математический аппарат для их описания применительно к теории поля.
"
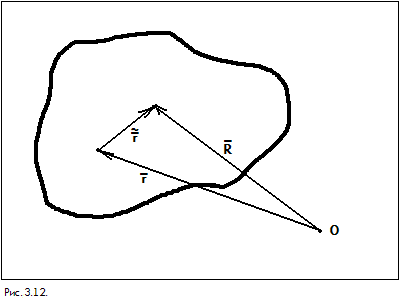Размажем"
заряд по пространству и введем внутри
этой области радиус-вектор, который
определяет плотность заряда в некоторой
точке:
.
Этот вектор
не
удобен для описания, поэтому введем
неподвижное начало координат "0",
из которого восстановим два вектора
и
.
Эти три вектора связаны соотношением:
.
Тогда плотность заряда будет зависеть
от разности
.
Но на данном этапе точечный заряд не
определен. Чтобы его ввести необходимо
представить плотность заряда в виде
.
Так как дельта-функция имеет пик в
области
,
весь заряд по сути собран в одной точке.
В этом случае можно записать
,
то есть заряд эквивалентен точечному,
но находится "во всем" пространстве.
Дельта-функция "отслеживает"
траекторию частицы, а, следовательно,
и движение точки, описываемой
.
Аналогичным образом введем трехмерный вектор плотности тока:
,
где
– фактическая скорость частиц.
Соответственно,
.
Введем четырехмерный вектор плотности тока следующим образом:
.
Следует иметь в виду тот факт, что
не является четырехмерным вектором.
Однако,
является четырехмерным вектором, так
как выше указанная дельта-функция
неинвариатна (таким образом, получено
нековариантное представление
четырехмерного вектора плотности тока).
Более удобным является представление четырехмерного вектора плотности тока в явно ковариантной форме:
.
Здесь
– инвариантный параметр, который, как
будет показано позже, перейдет в
собственное время.
Теперь следует убедиться, что полученное определение совпадает с полученным ранее. Перепишем его, выделив временную часть дельта-функции:
.
Необходимо снять интегрирование по , воспользовавшись для этого правилом интегрирования дельта-функции от сложного аргумента (дельта-функцию от сложного аргумента можно представить как
),
где
– корень уравнения
.
В нашем случае зависимость
от
однозначна, и, положив в производной
– корень этого уравнения – можно
записать:
.
Снимая интегрирование по
и учитывая тот факт, что
,
имеем
,
где – собственное время.
Данное выражение совпадает с тем, что
было получено для нековариантного
определения тока. Несложно убедиться
в том, что уравнение непрерывности
,
где
,
также выполняется.
§3.8. Четырехмерный вектор плотности силы.
При полевом представлении частиц вместо
четырехмерного вектора силы
,
которая действует на частицу, необходимо
использовать четырехмерный вектор
плотности силы
.
Рассмотрим, как вводится этот вектор на примере силы Лоренца, действующей на заряд во внешнем поле:
.
Если теперь поделить обе части на гамма-фактор, то будем иметь
,
где
,
а значит
.
Внеся
под знак интеграла и обозначив
,
запишем
.
Для того, чтобы выражение было ковариантным, необходимо перейти к интегрированию по четырехмерному объему , проинтегрировав обе части по времени. В итоге получим выражение
.
Найдем теперь компоненты четырехмерного вектора плотности силы. Положив и проведя суммирование, получим для пространственной компоненты
.
Обобщая, получаем выражение
.
Аналогично, для временной компоненты выражение принимает вид
.
То есть можно записать, что
.
Все компоненты четырехмерного вектора плотности силы найдены.