
экстремум
.doc4. Экстремум функции двух переменных
4.1 Необходимые условия существования экстремума.
Понятие максимума и минимума можно распространить и на случай функции нескольких переменных (здесь для случая двух переменных).
Говорят, что
функция
![]() имеет в точке
имеет в точке
![]() максимум
(минимум),
если существует такая окрестность точки
максимум
(минимум),
если существует такая окрестность точки
![]() ,
что для всех точек
,
что для всех точек
![]() из этой окрестности и отличных от точки
из этой окрестности и отличных от точки
![]() выполняется неравенство:
выполняется неравенство:
![]() ,
,
или
![]() .
.
Теорема 1
(Необходимые
условия существования экстремума). Если
функция
![]() имеет в точке
имеет в точке
![]() экстремум и в этой точке существуют
частные производные
экстремум и в этой точке существуют
частные производные
![]() и
и
![]() то
то
![]() (1)
(1)
Доказательство.
Из определения экстремума следует, что
![]() ,
рассматриваемая как функция одной
переменной
,
рассматриваемая как функция одной
переменной
![]() ,
при
,
при
![]() также имеет экстремум. Поэтому
также имеет экстремум. Поэтому
![]() .
Аналогично получаем равенство:
.
Аналогично получаем равенство:
![]() .
.
Замечание 1
Необходимое условие существования экстремума в случае дифференцируемой функции можно записать ещё и так:
![]() ,
,
в самом деле так
как, если
![]() ,
то каковы бы ни были
,
то каковы бы ни были
![]() ,
всегда выполняется
,
всегда выполняется
![]() .
(
.
(![]() )
)
И обратно: если в
данной точке тождественно выполняется
условие (![]() ),
то в виду произвольности
),
то в виду произвольности
![]() производные
производные
![]() порознь
также равны нулю.
порознь
также равны нулю.
Для случая более двух переменных соответственно имеем
![]()
и
![]()
Замечание 2
Приведенные условия существования экстремума не являются достаточными, о чем свидетельствует следующий
Пример
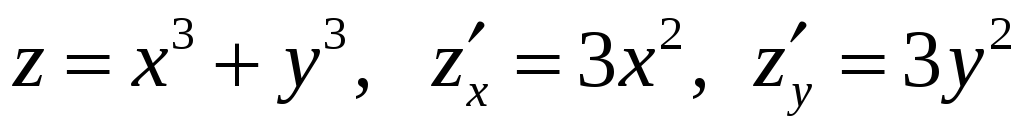 .
.
Частные производные
равны нулю в точке
![]() ,
но экстремума в этой точке функция не
имеет, так как в любой окрестности точки
,
но экстремума в этой точке функция не
имеет, так как в любой окрестности точки
![]() она принимает значения разных знаков,
а в самой этой точке
она принимает значения разных знаков,
а в самой этой точке
![]()
![]() .
.
4.2 Достаточные условия существования экстремума.
Теорема 1
(Достаточные
условия существования экстремума).
Пусть функция
![]() ,
непрерывная вместе со своими частными
производными первого и второго порядков
в некоторой окрестности точки
,
непрерывная вместе со своими частными
производными первого и второго порядков
в некоторой окрестности точки
![]() удовлетворяет условиям (1).
удовлетворяет условиям (1).
Обозначим
![]() .
.
Тогда в точке
![]() функция
функция
![]() :
:
-
имеет минимум, если
 и
и
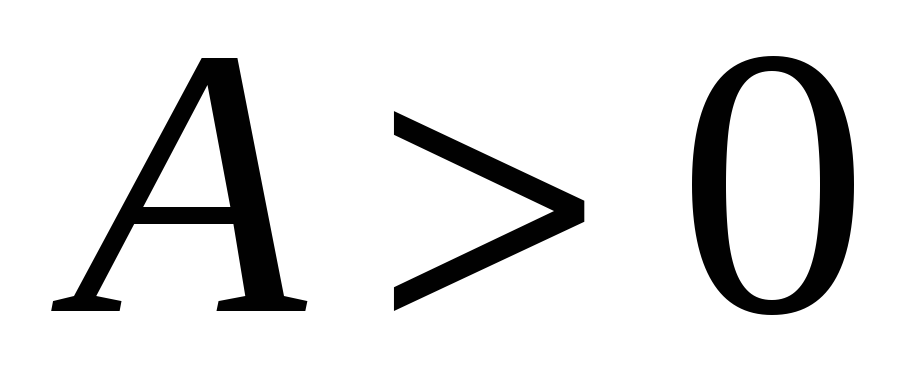 ;
; -
имеет максимум, если
 и
и
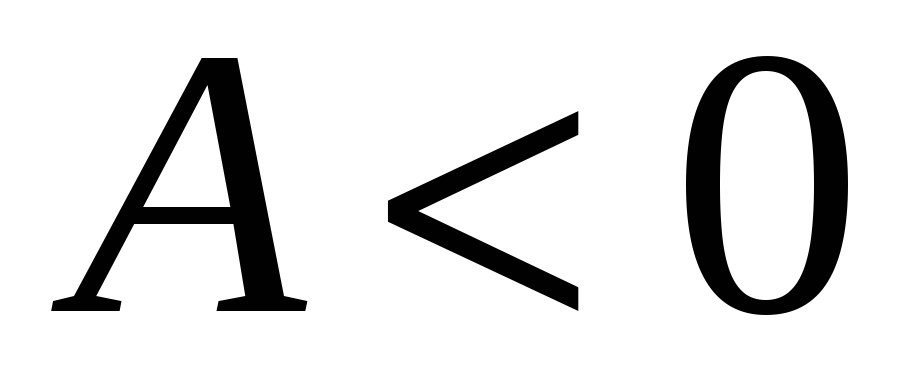 ;
; -
не имеет экстремума, если
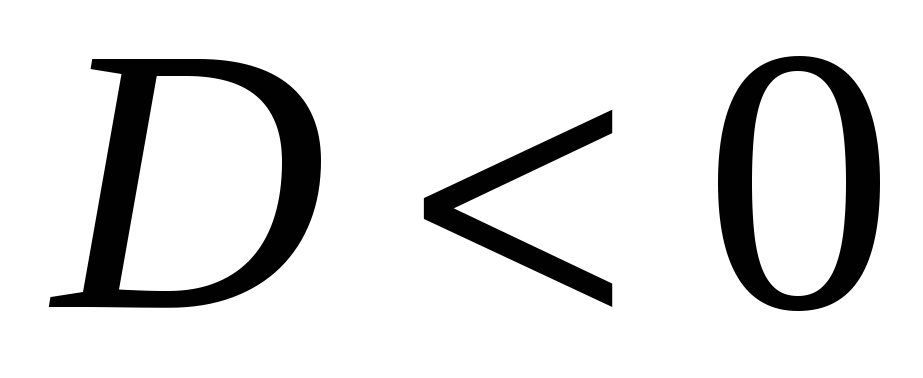
Доказательство
Ради краткости
доказательство проведем для случаев 1
и 2. Согласно формуле Тейлора, взятой
для
![]()
![]() ,
с учетом условий (1) имеем:
,
с учетом условий (1) имеем:
 (2)
(2)
где
![]()
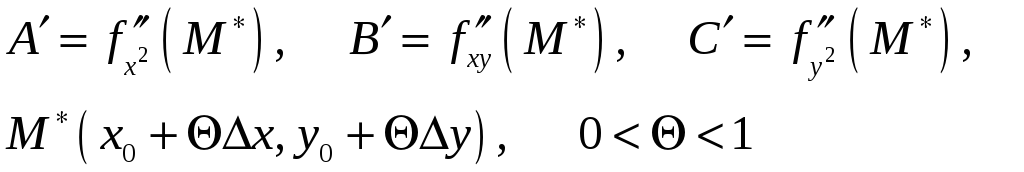
В силу непрерывности
вторых частных производных в точке
![]() следует, что
следует, что
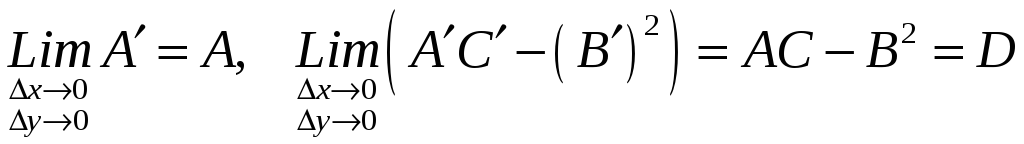 .
.
Поэтому в силу
свойств непрерывных функций для
достаточно малых
![]() имеем:
имеем:

В силу неравенств (3) и (4) равенство (2)можно представить в виде:

или дополняя до полного квадрата, в виде:
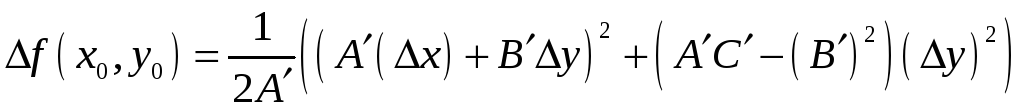
Выражение во
внешних скобках в силу неравенства (5)
положительно. Поэтому 1) если
![]() (а
тогда в силу неравенства (3) и
(а
тогда в силу неравенства (3) и
![]() ),
то
),
то
![]() ,
и следовательно, в точке
,
и следовательно, в точке
![]() минимум; 2) если
минимум; 2) если
![]() (а
тогда в силу неравенства (4) и
(а
тогда в силу неравенства (4) и
![]() ),
то
),
то
![]() ,
и следовательно, в точке
,
и следовательно, в точке
![]() максимум.
максимум.
Рассматривая
второй дифференциал (2) в рассматриваемой
точке он представляет собой однородный
многочлен второй степени или, как говорят
квадратичную форму от переменных
![]() и исследуя эту форму на знакоопределенности,
мы получаем ещё одно необходимое и
достаточное условие:
и исследуя эту форму на знакоопределенности,
мы получаем ещё одно необходимое и
достаточное условие:
Критерий Сильвестра (J.J. Sylvester)
Для того, чтобы (2) была определенной и положительной. Он выражается цепью неравенств
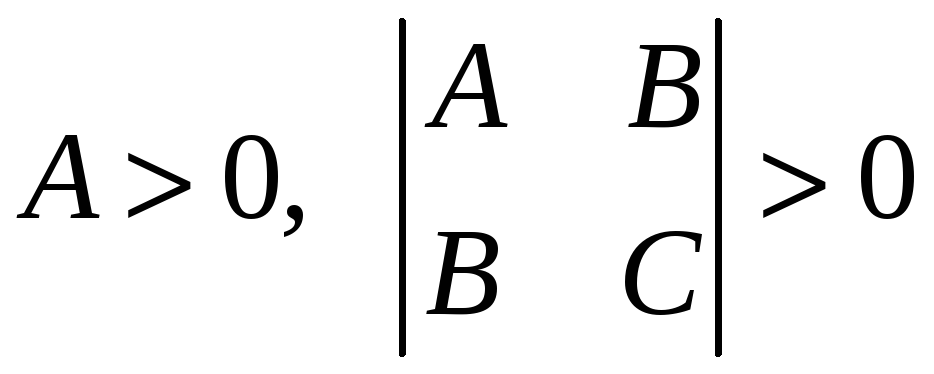 ,
,
а для определенной и отрицательной
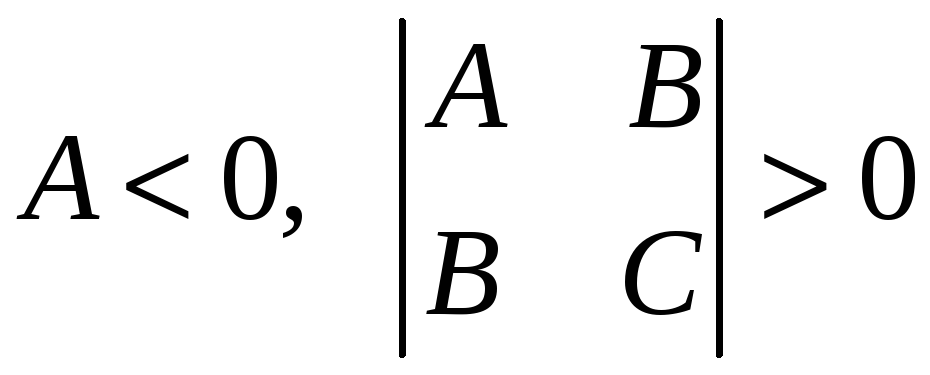 .
.
Пример 1
Исследовать на
экстремум функцию
![]() .
.
Решение: её частные
производные
![]() обращаются в нуль в точках
обращаются в нуль в точках
![]() и
и
![]() .
Её вторые производные равны
.
Её вторые производные равны
![]() .
В точке
.
В точке
![]() имеем
имеем
![]() и следовательно, в точке
и следовательно, в точке
![]() экстремума нет. В точке
экстремума нет. В точке
![]() имеем
имеем
![]() и следовательно, в точке
и следовательно, в точке
![]() минимум.
минимум.
Примечание.
Покажем на примерах, что в случае
![]() экстремум может быть, но его может и не
быть.
экстремум может быть, но его может и не
быть.
Пример 2
Функция
![]() в точке
в точке
![]() ,
где
,
где
![]() ,
как показано выше (см. п.4.1) экстремума
не имеет
,
как показано выше (см. п.4.1) экстремума
не имеет
Пример 3
Функция
![]() в точке
в точке
![]() ,
где
,
где
![]() ,
имеет экстремум, потому, что в любой
окрестности этой точки данная функция
положительна, а самой точке
,
имеет экстремум, потому, что в любой
окрестности этой точки данная функция
положительна, а самой точке
![]() равна нулю.
равна нулю.
