§3.6. II пара уравнений Максвелла в интегральной форме.

Вторая пара уравнений Максвелла имеет вид

.

Разберем сначала первое уравнение:

.

Проинтегрировав его по , получим

.

Неравенство нулю данного интеграла означает, что число линий напряженности , входящих в поверхность, в общем случае не равна числу линий, выходящих из нее. Это зависит от наличия и знака зарядов внутри поверхности.

С помощью данного уравнения можно достаточно легко вычислить напряженность электрического поля, создаваемого заряженным телом.

В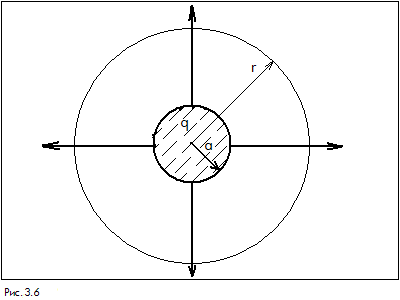 качестве примера рассмотрим шар радиуса , заряженный положительно зарядом . На самом деле следует рассмотреть два случая, когда рассматривается поле вне шара и внутри него.

Вне равномерно заряженного шара поле сферически симметрично. Выберем замкнутую поверхность в виде сферы радиусом (рис.3.6.). Уравнение Максвелла в интегральной форме выглядит как

.

В следствие сферической симметрии на всех точках выбранной сферы поле будет одинаково. Более того, векторы и сонаправлены:

,

а следовательно

.

Тогда уравнение можно переписать как

,

откуда следует, что

.

Собственно, получено уже известное выражение для поля однородно заряженного шара.

В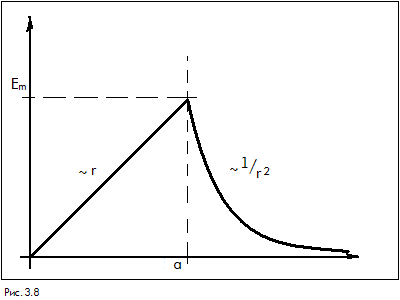 нутри шара поле также сферически симметрично. Выбрав сферическую поверхность внутри шара ( ) (рис.3.7.), применим к системе то же уравнение:

.

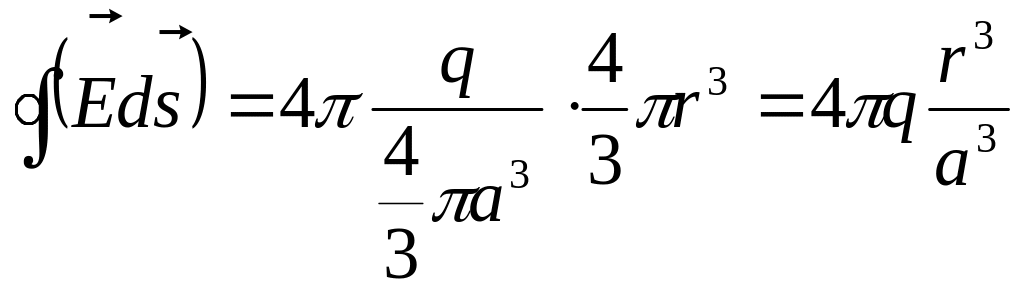Или, иначе,

для .

Таким образом, напряженность растет с ростом внутри шара, а затем вне шара спадает как (рис.3.8.).

Второе уравнение второй пары уравнений Максвелла в дифференциальной форме имеет вид:

.

Проинтегрировав его по незамкнутой поверхности с учетом теоремы Стокса получим выражение

и

,

где - полная плотность тока:

.

( - плотность омического тока, - плотность тока смещения.)

Если омический ток связан с перемещением зарядов, то ток смещения связан с переменными полями.

С помощью этого уравнения Максвелла в данном виде можно, например, вычислять напряженности магнитных полей проводников с током.

Рассмотрим для простоты постоянный ток в проводнике круглого сечения прямолинейной формы.

Как и в предыдущем примере с шаром, рассмотрим два случая – вне проводника и внутри него.

Будем считать, что электрический ток равномерный и постоянный. Окружим проводник поверхностью, которая будет иметь больший радиус, чем проводник (рис.3.9.). 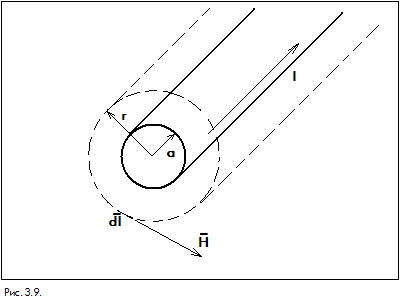Запишем уравнение для данного случая:

.

Из симметрии видно, что на всех точках окружности радиуса напряженность будет одинакова ( ). Также из симметрии видно, что вектора и сонаправлены. Исходя из этих рассуждений можно записать, что

(если ток постоянный, то ). Таким образом, получаем

,

откуда напряженность магнитного поля равна

.

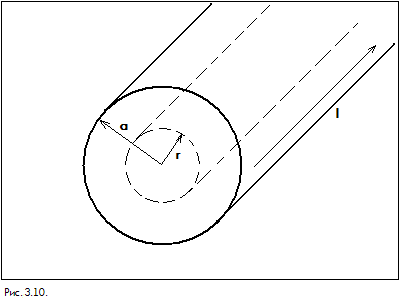
Е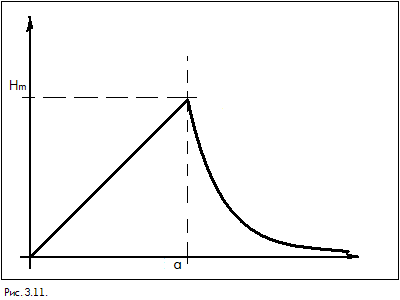 сли теперь рассматривать поверхность с радиусом (рис. 3.10), то очевидно, что по всей этой поверхности . Найдем поле внутри проводника. Уравнение принимает вид

.

Соответственно, выражение для тока в данном случае будет иметь вид

.

Следовательно, для напряженности магнитного поля внутри проводника имеем

.

Объединив оба случая ( и ) с учетом того условия, что на границе поля должны быть равны, получим зависимость значения поля от расстояния от центра проводника, которую схематично можно изобразить так, как это сделано на рис. 3.11.