§1.3. Преобразование Лоренца для координат и времени.

Необходимо определить такие преобразования инерциальных систем координат, чтобы . Этому условию удовлетворяют преобразования, для которых

.

Мы будем считать, что одна из точек, входящих в это преобразование, находится в начале координат. Покажем, что преобразования Галилея в таком случае не подходят:

.

Будем считать эти преобразования промежуточными (~), и позже они будут заменены на преобразования Лоренца. Подставим это преобразование в выражение для инварианта интервала:

.

Таким образом, видно, что инвариантность интервала при таком преобразовании не сохраняется, что противоречит утверждению об инвариантности интервала. Преобразуем теперь правую часть этого выражения к виду :

.

В последнем выражении была произведена замена:

Если теперь выразить и подставить в преобразование Галилея, получим в итоге преобразования

Согласно преобразованиям Галилея :

.

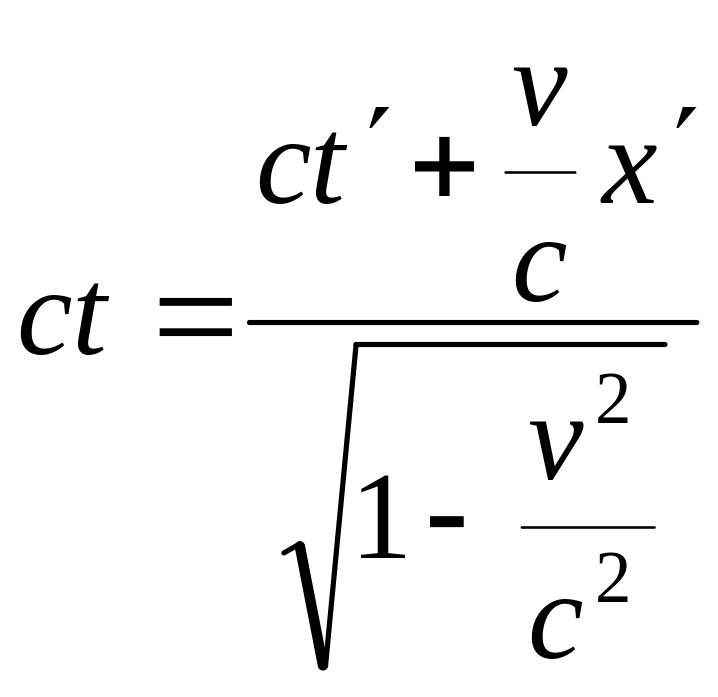Это и есть преобразование Лоренца для времени. Получим теперь преобразование Лоренца для координаты:

Окончательно, .

В итоге преобразование Лоренца для координат и времени выглядят следующим образом:

Для обратного преобразования, то есть перехода от к , следует только изменить знак у на и штрихованные величины сменить на нештрихованные. Несложно показать, что обратное преобразование Лоренца оставляет интервал инвариантом.

В нерелятивистском приближении преобразования Лоренца переходят в преобразование Галилея.

Действительно, будем считать, что , а следовательно :

Видно, что преобразования Галилея являются предельным случаем преобразования Лоренца, когда . То есть принцип соответствия между двумя теориями соблюден.

Если в системе частица покоится, то ее скорость относительно системы равна скорости системы относительно этой системы. То есть преобразование Лоренца выполняется для частиц, движущихся с релятивистскими скоростями.

Также нетрудно показать, что в нерелятивистском приближении выражение :

.

§1.4. Преобразования Лоренца для скоростей и углов.

После того как были получены преобразования Лоренца для координат и времени, следует определить преобразования Лоренца для скоростей и углов.

Если взять дифференциал от преобразований Лоренца для координат и времени, полагая .

Исходя из определения для скорости , получаем для проекций скоростей:

Эти выражения есть преобразования Лоренца для скоростей. Убедимся теперь, что в нерелятивистском приближении мы получим вновь преобразования Галилея, пренебрегая выражением :

Убедимся также, что преобразования Лоренца для скоростей не приводят к парадоксу как в преобразованиях Галилея:

_.

Перейдем теперь к преобразованиям Лоренца для углов. Рассмотрим случай больших скоростей. Пусть в системе частица покоится (рис. 1.13). Тогда скорость в проекциях на оси и можно представить как:

То же в системе:

Задача состоит в том, чтобы определить связь между и , для чего следует определит :

.

Будем считать теперь, что (это условие определения углов). Тогда

.

Чтобы избавиться от функции , запишем:

.

Откуда можно записать:

Аналогичным образом нетрудно показать, как выглядят преобразования Лоренца для телесного угла:

,

откуда можно напрямую записать, что

, где .