§3.9. Тензор плотности энергии и импульса частиц.
Ранее был определен четырехмерный вектор вида
.
В теории поля данная величина не
функционирует, и необходимо ввести
четырехмерный вектор плотности
энергии-импульса частиц. Введем сначала
четырехмерный вектор плотности силы
аналогично тому, как это было проделано
для
с той лишь разницей, что вместо
будет стоять
:
,
где
– произвольный инвариантный параметр.
Учитывая, что
,
перейдем к плотности энергии-импульса:
.
То есть
.
Найдем компоненты этого тензора:
.
Найдем компоненту
:
.
Обратим внимание на то, что тензор
симметричный.
,
.
Иногда для описания тензоров второго ранга используют диодное обозначение:
.
Тогда можно записать
,
где конструкция
не является, по сути, ни векторным, ни
скалярным произведением, а носит скорее
символический характер.
В матричной форме тоже самое можно переписать как
.
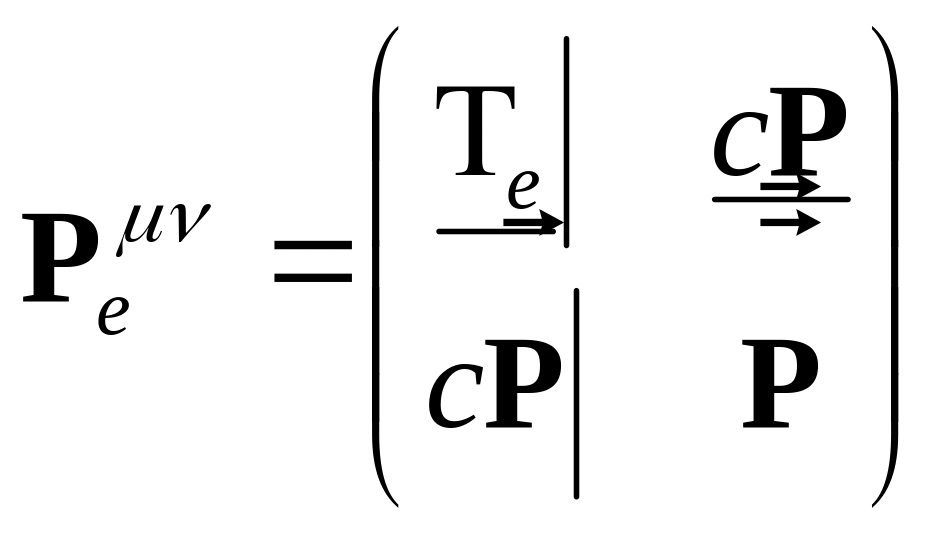§3.10. Тензор плотности энергии-импульса электромагнитного поля.
В качестве исходных соотношений воспользуемся второй парой уравнений Максвелла:
,
,
где
.
Получаем выражение
.
Путем простых преобразований несложно показать, что второй член в скобках принимает вид
.
Тогда выражение для запишется как
.
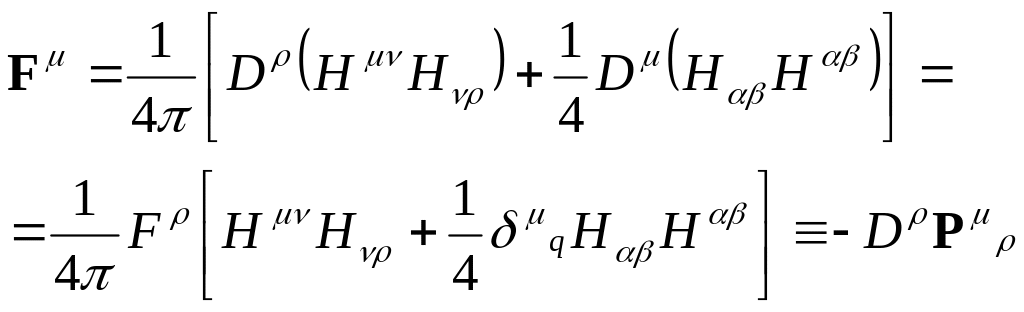Окончательно можно записать
–
плотность силы есть градиент со знаком "минус" от величины, которая есть плотность энергии-импульса электромагнитного поля. Эта величина имеет вид
.
Найдем компоненты полученного тензора:
–
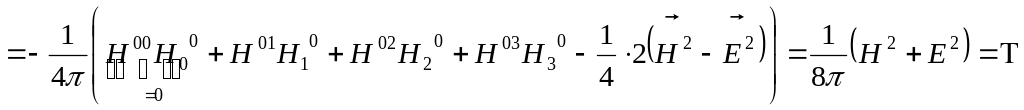плотность энергии электромагнитного поля.
,
или иначе
,
где
–
вектор Пойнтинга.
Найдем теперь в общем виде выражение
для
.
Вычислим сначала для случая
:
.
В случае, когда
имеем
.
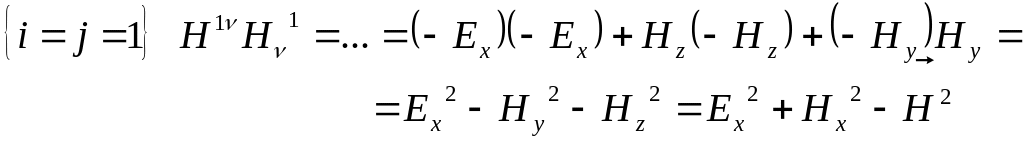То есть при
:
.
Обобщая оба случая, получаем
.
Теперь можно записать все компоненты для чисто пространственных индексов:
.
Тогда итоговое выражение выглядит как
.
Иногда это выражение также записывают в диодной форме:
.
В матричной форме то же самое можно записать как
.
§3.11. Закон сохранения плотности энергии-импульса в дифференциальной форме.
Известно, что плотность силы можно определить следующим образом:
– для частицы.
Но эту же величину можно записать как
– для поля.
Следовательно, получаем закон:
–
закон сохранения энергии-импульса в дифференциальной форме.
Покажем теперь, что из этого закона можно получить силу, которая действует на заряд в электромагнитном поле – силу Лоренца. Распишем плотность силы для частицы и для поля:
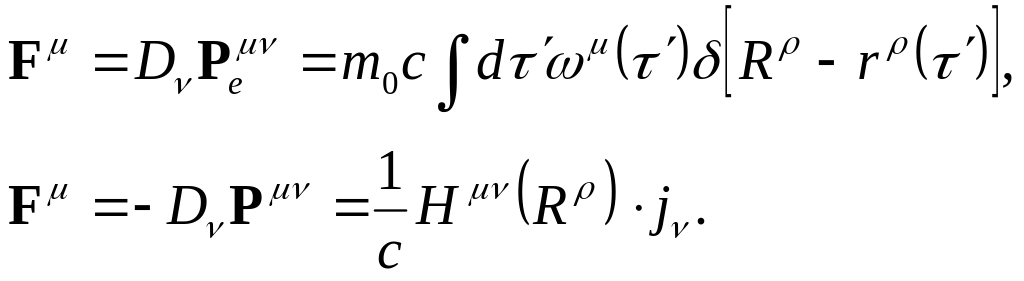
Подставим четырехмерный вектор плотности тока в интегральной форме в выражение для плотности силы для поля:
.
Теперь можно записать закон сохранения в виде
.
Нулю равно выражение в фигурных скобках, так как дельта-функция не является тождественно равной нулю. Таким образом, можно записать, что
,
то есть получена сила Лоренца.
Чтобы теперь перейти от теории поля к
теории частиц, необходимо проинтегрировать
по четырехмерному объему
:
.
Здесь интегрирование по
снято. Силу Лоренца можно обозначить
как
,
а
.
Так как внешнее поле от
не
зависит, то интеграл по
можно снять:
.
Получено выражение для четырехмерного вектора импульса. Значит выражение для закона сохранения энергии-импульса в дифференциальной форме верно.
Заметим, что в наиболее общем виде закон сохранения энергии-импульса записывается следующим образом:
.
В итоге получается уравнение движения с учетом радиационного трения (замедление движения за счет излучения).