
- •Глава I. Математический аппарат и основные понятия электродинамики.
- •§1.1. Постулаты специальной теории относительности.
- •§1.2. Четырехмерное пространство и четырехмерная символика.
- •§1.3. Преобразование Лоренца для координат и времени.
- •§1.4. Преобразования Лоренца для скоростей и углов.
- •§1.5. Кинематические «парадоксы» сто.
- •§1.6. Ковариантные формы преобразований Лоренца.
- •§1.7. Четырехмерные векторы.
- •§1.8. Четырехмерные тензоры.
- •§1.9. Четырехмерный вектор-потенциал и тензор напряженности электромагнитного поля.
- •§1.10. Инварианты электромагнитного поля.
- •Глава II. Релятивистская механика.
- •§2.1. Четырехмерные векторы импульса и силы.
- •§2.2. Вариационный принцип Гамильтона в релятивистской механике.
- •§2.3. Вывод силы Лоренца.
- •§2.4. Релятивистские уравнения Гамильтона.
- •§2.5. Законы сохранения и свойства симметрии четырехмерного пространства.
- •§2.6. Тензор спина и малая группа Лоренца.
- •§2.7. Четырехмерный вектор спина.
- •§2.8. Уравнение Баргмана-Мишеля-Телледи.
- •Глава III. Полевая электродинамика.
- •§3.1. I пара уравнений Максвелла в дифференциальной форме.
- •§3.2. Вариационный принцип Гамильтона в теории поля.
- •§3.3. II пара уравнений Максвелла в дифференциальной форме для "чистого" поля.
- •§3.4. II пара уравнений Максвелла при наличии зарядов и токов.
- •§3.5. I пара уравнений Максвелла в интегральной форме.
- •§3.6. II пара уравнений Максвелла в интегральной форме.
- •§3.7. Четырехмерный вектор плотности тока.
- •§3.8. Четырехмерный вектор плотности силы.
- •§3.9. Тензор плотности энергии и импульса частиц.
- •§3.10. Тензор плотности энергии-импульса электромагнитного поля.
- •§3.11. Закон сохранения плотности энергии-импульса в дифференциальной форме.
- •§3.12. Вектор Пойнтинга.
- •§3.13. Тензор натяжений Максвелла.
- •§3.13. Законы сохранения в дифференциальной форме как следствие однородности и изотропности пространства.
- •§3.16. Орбитальный и спиновый угловые моменты электромагнитного поля.
- •Глава IV. Теория частиц и полей.
- •§4.1. Об устойчивости статической системы электрических зарядов.
- •§4.2. Собственная масса замкнутой системы частиц и полей.
- •§4.3. Электромагнитная масса электрона.
Глава IV. Теория частиц и полей.
§4.1. Об устойчивости статической системы электрических зарядов.
Простейший случай одноименных зарядов является неустойчивой системой, так как они будут отталкиваться друг от друга с кулоновской силой
![]() .
.
Р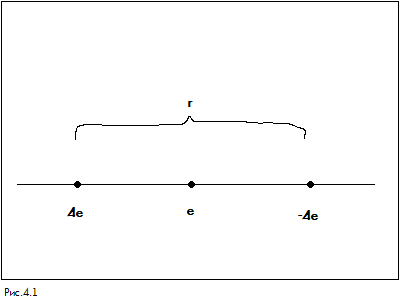 азноименные
заряды будут притягиваться друг к другу
и в конце концов упадут друг на друга.
азноименные
заряды будут притягиваться друг к другу
и в конце концов упадут друг на друга.
Рассмотрим расположение трех зарядов, изображенное на рис.4.1. Эта система квазиустойчива. Для устойчивого положения сила отталкивания должна компенсировать силу притяжения:
 .
.
Однако, эта система неустойчива, так как равенство справедливо только для стационарного состояния. Если же один из зарядов сместить, то система выйдет из состояния равновесия, в которое уже не вернется.
По этому поводу существует теорема Ирншоу, которая гласит, что существование устойчивой стационарной системы зарядов невозможно.
Идея доказательства состоит в нахождении потенциальной энергии системы и доказательстве того, что она не имеем минимума, откуда и следует неустойчивость системы.
Действительно, энергия системы может быть найдена как
![]() .
.
Для системы электростатических зарядов
![]() .
.
Тогда энергия запишется как
![]() .
.
Для того, чтобы энергия системы имела минимум, необходимо, во-первых, чтобы все первые производные по координатам зарядов были равны нулю и, во-вторых, все вторые производные от потенциальной энергии были положительными.
Оказывается, что сумма всех вторых производных равняется нулю:
![]() ,
,
что автоматически означает отсутствие минимума потенциальной энергии. докажем, что это соотношение имеет место.
Рассмотрим сначала ситуацию, когда
![]() и
и
![]() .
Тогда производные берутся по "чужим"
переменным и они всегда дают нуль.
.
Тогда производные берутся по "чужим"
переменным и они всегда дают нуль.
В случае, когда
![]() или
или
![]() ,
тогда
,
тогда
![]() .
.
Следовательно, вышеуказанное равенство действительно имеет место и минимума потенциальной энергии нет – существование устойчивой системы невозможно.
§4.2. Собственная масса замкнутой системы частиц и полей.
В дальнейшем мы будем рассматривать динамические устойчивые системы.
Замкнутой системой называется система островного типа, которая не теряет ни энергию, ни импульс, а также не получает их извне. Как известно, мощность можно записать как
,
где
![]() – вектор Пойнтинга.
– вектор Пойнтинга.
Если вектор Пойнтинга равен нулю, то энергия не теряется, а претерпевает превращения внутри системы. Тогда и потери импульса
![]() .
.
Если эти условия выполняются, то мы будем иметь закон сохранения энергии и импульса системы:
![]() .
.
Очевидно, что
 .
.
Эти законы можно объединить в один закон сохранения четырехмерного вектора импульса всей системы:
![]() .
.
Если и объединяются в , то имеет место соотношение
![]() ,
,
где
![]() – суммарная масса в системе, где центр
тяжести находится в состоянии покоя. С
помощью этого соотношения можно найти
массу системы:
– суммарная масса в системе, где центр
тяжести находится в состоянии покоя. С
помощью этого соотношения можно найти
массу системы:
![]() ,
,
тогда
![]() –
–
масса динамической системы.
Так как масса системы есть инвариантная величина, проще всего ее выписать в системе покоя центра тяжести (центра инерции).
В случае одного электрона имеем:
 .
.
Тогда выражение для массы примет вид
![]()
или, если расписать
![]() и
и
![]() ,
,
![]() –
–
полевая масса. Обозначив полевую массу
через
![]() ,
можно записать
,
можно записать
![]() .
.
Если заряд считать точечным, то
![]() и
и
![]() .
.
Радиус электрона не может быть бесконечно малой величиной и его можно определить из условия, чтобы величина имела порядок массы самого электрона:
![]() .
.
Определим из этого соотношения
![]() :
:
![]() .
.
На расстояниях
![]() классическая электродинамика перестает
работать.
классическая электродинамика перестает
работать.
Известно, что
![]() .
.
В теореме Ирншоу было получено выражение
![]() .
.
Получим его другим способом:
![]() ,
,
где
![]() – потенциал в точке, где находится
-й
заряд. Он создается в ней всеми остальными
зарядами. В свою очередь
– потенциал в точке, где находится
-й
заряд. Он создается в ней всеми остальными
зарядами. В свою очередь
![]() ,
,
где
![]() – потенциал всех остальных зарядов в
точке
– потенциал всех остальных зарядов в
точке
![]() .
То есть
.
То есть
![]() .
.
Множитель
![]() появляется за счет того, что взаимодействие
заряженных частиц является парным. В
частности для случая двух зарядов имеем
появляется за счет того, что взаимодействие
заряженных частиц является парным. В
частности для случая двух зарядов имеем
![]() –
–
потенциальная энергия взаимодействия двух зарядов. Подставим это выражение в формулу для массы всей системы:
![]() ,
,
![]() .
.
Распад системы влечет за собой рост кинетической энергии.
