4.3.9 Ламинарное и турбулентное течение жидкости

Мы уже обсуждали, что наблюдается два течения жидкости или газа: ламинарное течение жидкости и турбулентное. Обычно ламинарное течение жидкости устанавливается в трубках с гладкими стенками без резких изменений площади сечений и резких изгибов трубки. При нарушении этих условий, а особенно при высоких скоростях, течение жидкости переходит в турбулентное, т.е. вихревое (см. рис. 4.1). Скорость течения жидкости будет разной в разных точках спирали, значит, будут наблюдаться местные изменения давления в жидкости, вызывающие колебательные движения частиц, сопровождающиеся звуковыми явлениями (шум, журчание), благодаря этому турбулентное течение легко обнаруживается.

Английский ученый Рейнольдс установил, характер течения зависит от значения безразмерной величины:

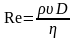, (4.5)

где  – плотность жидкости или газа, – средняя по сечению трубы скорость потока,  – коэффициент вязкости жидкости, D – характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус при круглом сечении.

Величина Re называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдается ламинарное течение жидкости. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера для круглой трубы взять ее диаметр, то критическое значение числа Рейнольдса оказывается примерно 2000. Характер течения различных жидкостей или газов в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение числа Рейнольдса.

4.3.10 Формула Пуазейля

Объем жидкости, протекающей через поперечное сечение круглой трубы в единицу времени при ламинарном течении зависит от вязкости жидкости, разности давлений и размеров трубки, по которой течет жидкость. Обозначим dQ – объемную скорость жидкости, эта скорость равна объему жидкости, протекающему через поперечное сечение трубки в единицу времени:

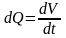. (4.6)

Найдем связь между линейной и объемной скоростями жидкости. Выделим в трубке небольшой объем в форме цилиндра, площадь поперечного сечения этого цилиндра равна dS, а длина равна dl, тогда объем этого цилиндра 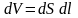. Длину цилиндра можно выразить через линейную скорость течения жидкости следующим образом 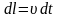, тогда 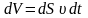. Подставим это выражение в уравнение (4.6), получим:

. (4.7)

Таким образом, объемная скорость течения жидкости по сосуду равна линейной скоростью течения жидкости умноженной на площадь поперечного сечения.

Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра. Французский врач Жан Луи Мари Пуазейль работал по вопросам кровообращения и дыхания, поэтому заинтересовался вопросами гидродинамики. Им была получена формула, которая получила название формулы Пуазейля, которая устанавливает связь между объемной скоростью течения жидкости, вязкостью жидкости и разностью давлений на концах цилиндрической трубки при ламинарном течении жидкости:

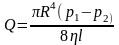, (4.8)

где R – внутренний радиус трубки, по которой течет жидкость, 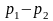– разность давлений на концах трубки,  – вязкость жидкости, текущей по трубке.

Если бы жидкость не обладала вязкостью, то для течения по горизонтальной трубе не требовалось бы прилагать ни какую силу, но благодаря вязкости стационарное течение любой реальной жидкости в трубе возможно лишь тогда, когда между концами трубы создана разность давлений – будь это вода в водопроводной воде или кровь в кровеносной системе.

Согласно формуле Пуазейля, поток жидкости Q пропорционален градиенту давления 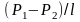и обратно пропорционален вязкости жидкости (газа), чего и следовало ожидать. Однако может показаться удивительным, что Q зависит от четвертой степени радиуса трубы. Это означает, что при одном и том же градиенте давления увеличение радиуса трубы вдвое приведет к увеличению потока в шестнадцать раз! Таким образом, даже небольшое изменение радиуса трубы приводит к значительному изменению потока жидкости; для того же, чтобы поддерживать поток на прежнем уровне, пришлось бы заметно изменить разность давлений.

Интересный пример зависимости вида R⁴ можно найти в системе кровообращения человеческого организма. Однако, поскольку формула Пуазейля справедлива лишь для ламинарного течения несжимаемой жидкости с постоянной вязкостью , она не может в точности выполняться для крови; дело в том, что течение крови не вполне ламинарно, кровь содержит взвешенные частицы, диаметр которых почти равен диаметру капилляров, а ее вязкость  зависит от скорости течения . Тем не менее, и в этом случае формула Пуазейля является хорошим приближением в первом порядке. Поток крови в организме регулируется крошечными мышцами, окружающими сосуды. При сокращении этих мышц диаметр сосуда уменьшается и поток, который в соответствии с формулой Пуазейля пропорционален R⁴, резко уменьшается уже при небольшом уменьшении радиуса. Таким образом, едва заметными сокращениями этих мышц очень точно контролируется поступление крови к различным органам. Однако если, скажем, вследствие атеросклероза (затвердевания стенок сосудов) и отложений холестерина радиус сосудов уменьшается, то для поддержания нормального кровотока требуется более высокий градиент давления. Если радиус сосудов уменьшится вдвое, то сердцу придется увеличить давление в 16 раз. В таких условиях сердце работает с перегрузкой, но, как правило, уже не может обеспечить требуемую величину потока жидкости, т.е. нормальное кровообращение.

Таким образом, повышенное артериальное давление указывает и на то, что сердце работает с перегрузкой, и на то, что поток крови через артерии ниже нормы.