3.4 Полная энергия собственных колебаний

В простых гармонических колебаниях происходит непрерывный переход потенциальной энергии в кинетическую энергию, и обратно; полная энергия колеблющейся системы сохраняется, если в системе отсутствуют силы трения.

Выясним, как изменяется со временем кинетическая 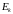и потенциальная 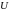энергия гармонического колебания на примере упругой пружины. Кинетическая энергия равна (см. выражения (2.18) и (3.2))

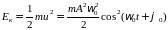. (3.10)

Потенциальная энергия выражается формулой (см. выражения (2.21) и (3.1))

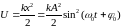. (3.11)

Складывая (3.9) (3.10) , с учетом соотношения (3.6) получим:

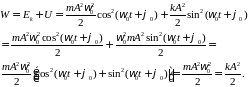(3.12)

Из соотношения (3.12) видно, что полная энергия свободных колебаний равна максимальной потенциальной энергии или максимальной кинетической энергии гармонических колебаний и прямо пропорциональна массе колеблющейся точки , квадрату амплитуды 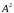и квадрату частоты колебания.

3.5 Сложение колебаний, направленных вдоль одной прямой

Возможны случаи, когда на тело действуют несколько упругих сил. Каждая из этих сил заставляет тело совершать гармоническое колебание. При одновременном воздействии этих сил тело одновременно будет участвовать во всех этих движениях. Примером может служить барабанная перепонка, одновременно воспринимающая множество звуковых колебаний. В этом случае, чтобы найти результирующее движение, необходимо сложить колебания.

Рассмотрим случай, когда тело одновременно участвует в двух колебаниях с одинаковыми частотами, но разными амплитудами и начальными фазами:

,

.

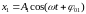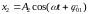Результирующее колебание также является гармоническим и определится суммой смещений

.

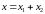Рисунок 3.4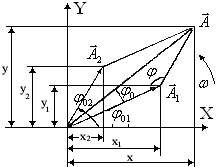

Для определения результирующего смещения применяется векторный метод сложения колебаний (см. рисунок 4), так как любое гармоническое колебание можно описать с помощью радиус – вектора, модуль которого равен амплитуде колебания (см. раздел 3.1).

Углы отсчитывается от положительного направления оси ОХ. На рисунке 3.4 изображены положения векторов 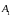и 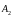в начальный момент 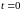, т.к векторы вращаются с одинаковой угловой скоростью, то и их результирующий вектор будет вращаться с той же угловой скоростью, т.е., результирующее движение также будет гармоническим с круговой частотой :

.

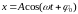Амплитуду этого колебания можно найти по теореме косинусов:

,

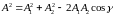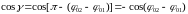, поэтому

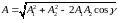. (3.13)

Начальную фазу результирующего колебания можно определить из начальных условий:

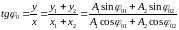. (3.14)

Анализируя уравнение (3.13), видим, что при сложении одинаково направленных колебаний возможны следующие случаи:

1. если разность фаз равна четному числу , т.е.

,

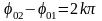где 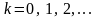(можно считать, что 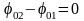), то колебания совпадают по фазе и усиливают друг друга. В этом случае

Рисунок 3.5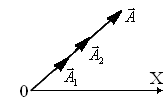

,

,

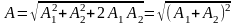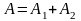т.е. результирующая амплитуда равна сумме амплитуд составляющих колебаний (см. рисунок 3.5).

2. При разности фаз, равной нечетному числу 

, ,

,

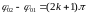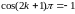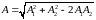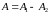, (3.15)

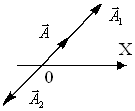
Рисунок 3. 6

т.е. колебания ослабляют друг друга и результирующая амплитуда равна разности амплитуд складываемых колебаний (см. рисунок 3.6). При , т.е., если амплитуды складываемых колебаний одинаковы и колебания совершаются в противофазе, то колебания друг друга гасят.

3) Если складываемые колебания имеют одинаковые амплитуды (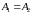 ), но частоты складываемых колебаний не одинаковы, то результирующее колебание не будет гармоническим.

Рисунок 3.7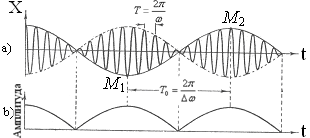

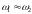Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте . Результирующее колебание при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой (см. рисунок 3.7). Такие колебания называются биениями. График изменения амплитуды со временем показан на рисунке 3.7б.