2.3.3 Равномерное распределение
Определение равномерного распределения. Случайная величи-
на имеет равномерное распределение на отрезке [a; b] , если ее плотность
распределения вероятностей постоянна и равна C на указанном отрезке,
а вне отрезка плотность распределения равна нулю.
Числа a, b являются границами возможных положительных значений
данной случайной величины. Левая граница a служит параметром положе-
ния, а разность b − a параметром масштаба. Параметры распределения
отличают одно конкретное равномерное распределение от другого.
Равномерное распределение реализуется, например, в практических за-
дачах, где случайным образом выбирается точка на отрезке [a; b] или прово-
дится округление чисел.
Воспользуемся условием нормировки, справедливым для любой плот-
ности распределения вероятностей и найдём значение постоянной C
+∞
∫
f (x)dx = 1 ⇒
−∞
b
∫
a
f (x)dx = 1 ⇒ C (b − a) = 1 ⇒ C = 1/(b − a).
56
Итак, плотность равномерного распределения задаётся формулой
f (x) = 1/(b − a), если x ∈ [a; b]; f (x) = 0, если x /∈ [a; b].
На Рис. 6 для примера представлен график функции плотности равномер-
ного распределения с нижней границей a = 0 и верхней границей b = 2 .
Рис. 6
Функция распределения выражается через плотность как интеграл с
переменным верхним пределом и задается следующей формулой:
0, x < a,
x
∫
du
x−a
F (x) =
a
b−a=b−a, a≤ x ≤ b,
-
,
x > b.
Данная функция распределения является кусочно-линейной функцией, воз-
растающей от нуля в точке (a, 0) до единицы в точке (b, 1) .
На Рис. 7 для примера представлен график функции распределения
равномерно распределенной случайной величины со значениями нижней гра-
ницы a = 0 и верхней границы b = 2 .
Математическое ожидание находим по определяющей формуле в виде:
b
mx= M (X ) =
1
b − a
∫
a
x dx =
57
b2 − a2
2(b − a)
=
a + b
2
.
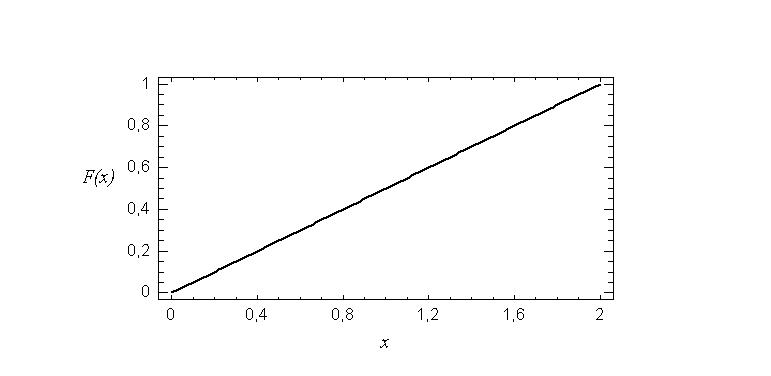
Рис. 7
Так как функция распределения на отрезке [a; b] строго возрастает,
то медиана hxвычисляется как единственное решение уравненияxb−−aa=12
в виде hx= (a + b)/2 . Видно, что медиана находится в центре плотности
распределения и совпадает с математическим ожиданием.
Мода распределения определяется неоднозначно и может быть равна
любому числу от нижней границы a до верхней границы b .
Вычисление дисперсии обычно проводится по формуле, представляю-
щей дисперсию как разность второго начального момента и квадрата мате-
матического ожидания
Dx=
+∞
∫
x2f (x)dx − m2x=
−∞
1
b − a
b
∫
a
x2dx −
(a+ b)2
4
=
(b − a)2
12
.
√
Стандартное отклонение равно корню из дисперсии: σx= (b − a)/2
Из уравнения F (x) =x−a 1
3 .
b−a=4 находим нижний квартиль распределе-
ния в виде x0,25 = (3a + b)/4 . Аналогично, из уравнения F (x) =xb−−aa=34
вычисляем верхний квартиль в виде x0,75= (a + 3b)/4 . Отсюда, интерквар-
тильный размах имеет значение w0,5=x0,75 − x0,25= (b − a)/2 , а серединное
отклонение Ex= w0,5/2 = (b − a)/4 .
Так как равномерное распределение симметрично относительно мате-
матического ожидания, то коэффициент асимметрии равен нулю.
Коэффициент эксцесса меньше нуля, так как равномерное распределе-
ние является менее островершинным, чем нормальное распределение.
58