2.2.4 Биномиальное распределение

Случайная величина имеет биномиальное распределение с параметра-

ми n и p , если она принимает значения 0, 1, 2, . . . , n c вероятностями

P (X = k) = p_k= C_nk_pk_qn−k_,k = 0, 1, . . . , n; q = 1 − p.

Данные вероятности называют биномиальными, поскольку они являются

n

членами разложени бинома Ньютона (q + p)ⁿ= ∑ C_nk_pk_qn−k , а формулу

k=0

вычисления биномиальных вероятностей называют формулой Бернулли.

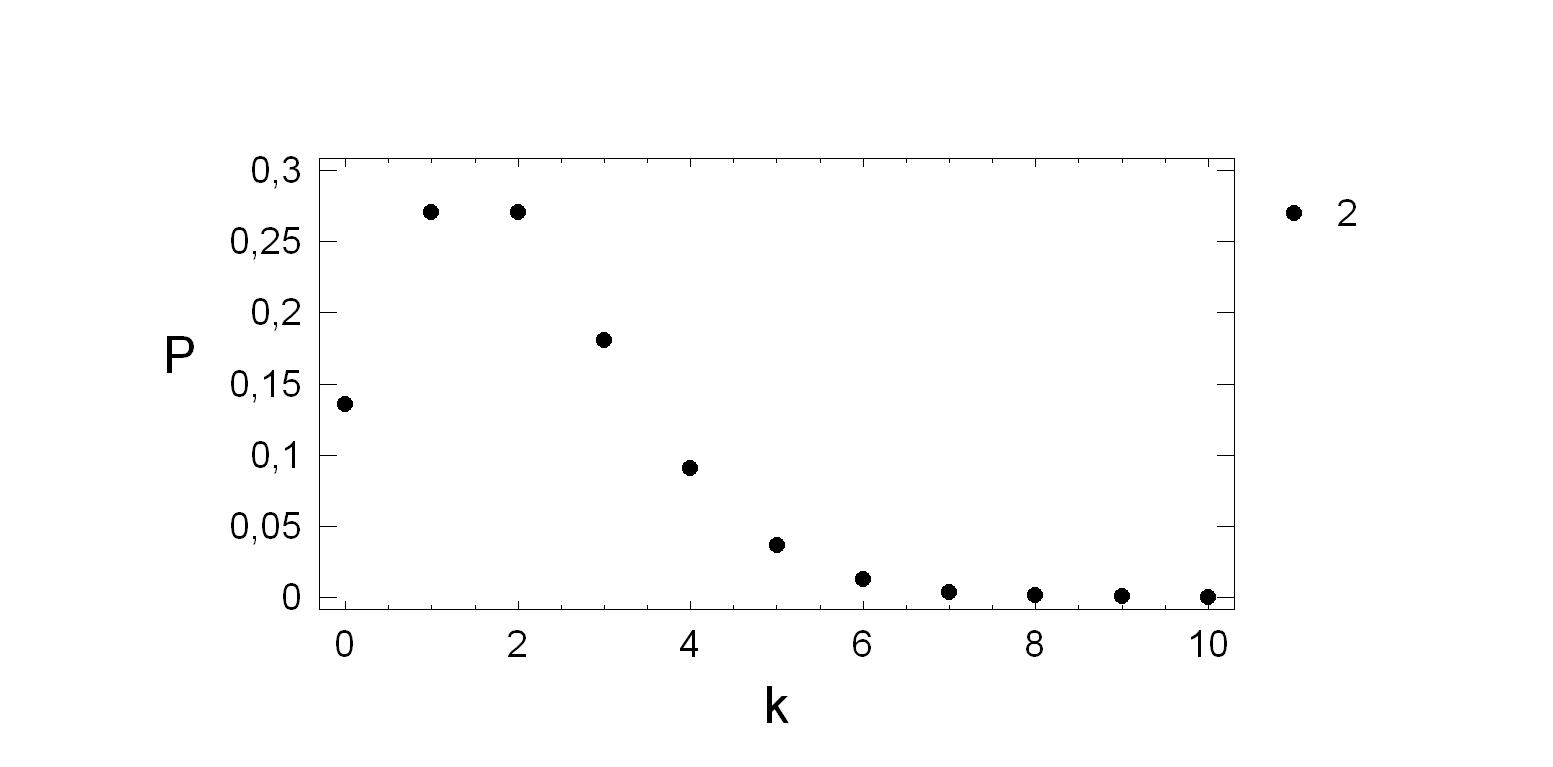
На Рис. 1 представлен график биномиального распределения при зна-

чениях параметров n = 10 , p = 0, 1 .

Рис. 1

Биномиальная случайная величина обычно рассматривается в рамках

схемы Бернулли, когда проводятся n независимых испытаний, в каждом

из которых интересующее наблюдателя событие A (ѕУспехї) появляется с

вероятностью p и не появляется AЇ (ѕОтказї) с вероятностью q = 1 − p .

В данной схеме параметр биномиального распределения p является вероят-

ностью ѕУспехаї, а значение q = 1 − p является вероятностью ѕОтказаї.

42

Изменяя значения параметров n и p переходят от одного конкретного бино-

миального распределения к другому.

В теории надежности биномиальное распределение используется при

анализе испытаний изделий по схеме ѕУспех-Отказї, в задачах контроля ка-

чества продукции при выборочном контроле партии из n приборов, в бал-

листике при оценке числа попаданий в цель и т. д.

Биномиальная случайная величина B_n,p(ω) задает число появлений со-

бытия A в n независимых испытаниях и, по общему определению случайной

величины, является отображением пространства элементарных событий Ω в

числовое множество {0, 1, 2, . . . , n} . Если обозначить отказ при некотором

испытании цифрой 0 , а успех цифрой 1 , то каждый элемент простран-

ства Ω будет представлять собой конечную последовательность из нулей и

единиц длиной n , т. е. пространство Ω будет иметь вид:

Ω = {(0, 0, . . . , 0, 0), (0, 0, . . . , 0, 1), (0, 0, . . . , 1, 0), . . . , (1, 1, . . . , 1, 1)}.

Вероятность любого соединения, содержащего k успехов и, соответственно,

n − k отказов подсчитывается по формуле умножения независимых событий

и равна p^kqⁿ−k . Данные соединения попарно несовместны, а их количество

равно числу способов расставить k единиц на n местах, т. е. числу сочетаний

из n по k . По формуле сложения C_nk несовместных событий с одинаковыми

вероятностями p^kqⁿ−k получим, что вероятность события ѕПоявится ровно k

успеховї равна C_nk_pk_qn−k . Отсюда, учитывая, что число k принимает зна-

чения 0, 1, 2, . . . , n , следует, что ряд распределения биномиальной случайной

величины имеет вид, указанный в исходном определении.

Отметим, что распределение Бернулли является частным случаем би-

номиального распределения, когда параметр n равен единице.

По общему определению, функция распределения F_B(x) биномиальной

случайной величины имеет следующий вид:



 0, x ≤ 0,





F_B(x) = P {B(ω) < x} = ∑_pk⁼

k<x



∑ C_nk_pk_qn−k_,0 < x ≤ n,

k<x

 ,

x > n.

Таким образом, функция распределения F_B(x) является непрерывной слева,

кусочно-постоянной функцией, возрастающей от нуля до единицы. В каждой

точке k = 0, 1, . . . , n функция F_B(x) имеет разрыв первого рода, причем

скачок функции равен P (X = k) = p_k= C_nk_pk_qn−k_.

43

Формулы вычисления математического ожидания и дисперсии

выводятся с помощью производящей функции:

ϕ(x) =

n

∑

k=0

n

p_kx^k= ∑

k=0

C_nk_pk_qn−k_xk_{= (}q + px)ⁿ.

Отсюда: ϕ⁰(x) = n(q + px)ⁿ−1_p, ϕ⁰⁰(x) = n(n − 1)(q + px)ⁿ−2_p2 . Так

как q + p = 1 , то справедливы формулы: ϕ⁰(1) = np , ϕ⁰⁰(1) = n(n − 1)p².

Используя выражения для вычисления математического ожидания и

дисперсии через производные производящей функции, получим:

m = ϕ⁰(1) = np,

00

0

0

D = ϕ (1) + ϕ (1) − ϕ (1)²= n(n − 1)p²+ np − (np)²= np(1 − p) = npq.

Стандартное отклонение по определению вычисляется как корень

квадратный из дисперсии в следующем виде:

√

σ = Ⲛ_np(1 − p) =

npq.

Мода биномиального распределения d находится по общему опре-

делению. В зависимости от значений параметров n и p биномиальное рас-

пределение может быть как симметричным (коэффициент асимметрии

равен нулю), так и несимметричным (коэффициент асимметрии от-

личен от нуля). Если параметры биномиального распределения такие, что

возможна аппроксимации биномиального распределения нормальным рас-

пределением, то коэффициент эксцесса данного конкретного биноми-

ального распределения близок к нулевому значению. В остальных слу-

чаях коэффициент экцесса вычисляется по определяющей формуле и сильно

зависит от значений параметров n и p .

Вычисления вероятностей непосредственно по формуле Бернулли при

больших значениях n и p приводят к арифметическим операциям с больши-

ми числами, что вызывает повышенную вычислительную погрешность. До-

полнительная погрешность вычислений возникает также при значениях пара-

метра p , близких к нулю или единице. Для проведения расчетов в указанных

случаях были выведены формулы, аппроксимирующие формулу Бернулли и

имеющие достаточно высокую точность.

Биномиальное распределение с параметрами n и p может быть ап-

проксимировано нормальным распределением с математическим ожи-

данием np и стандартным отклонением Ⲛ_np(1 − p) , если только выполня-

ются условия np(1 − p) > 5 и 0, 1 < p < 0, 9 . При условии np(1 − p) > 25

это приближение можно применять при любых p .

44

Если значение параметра p мало, а значение параметра n велико так,

что p < 0, 1 и np ≤ 10 , то биномиальное распределение приближают

распределением Пуассона со значением параметра λ = np .

Пример. Куплено два лотерейных билета, причем известно, что ве-

роятность выигрыша по каждому билету равна 0, 6 . Найти для случайной

величины ѕЧисло выигрышейї и соответствующего конкретного биномиаль-

ного распределения при значениях параметров n = 2 , p = 0, 6 : случайную

величину; ряд и функцию распределения; полигон и график функции распре-

деления; основные числовые характеристики положения, рассеяния и формы;

вероятность попадания случайной величины на полуинтервал [m − σ; m + σ) .

Решение. В данном случае вероятностное пространство имеет вид

Ω = {(0, 0), (0, 1), (1, 0), (1, 1)},

где цифрой 0 обозначено отсутствие выигрыша по билету, а цифрой 1

выигрыш по билету. Биномиальная случайная величина B_2;0,6⁽ω) отображает

пространство Ω в числовое множество {0,1,2} таким образом, что исходу

(0, 0) соответствует значение случайной величины ноль, исходам (0, 1), (1, 0)

значение единица, а исходу (1, 1) значение два.

Вероятность исхода (0, 0) вычисляется по правилу умножения незави-

симых событий P (0, 0) = P (0)·P (0) = q · q = q²= 0, 16 или по определяющей

формуле P (B = 0) = p₀= C₂0_p0_q2_{= 1}· 1 · q²= q²= 0, 16 .

Далее, используя правило сложения несовместных событий и правило

умножения независимых событий, получим, что событие {(0, 1)+ (1, 0)} име-

ет вероятность P {(0, 1)+(1, 0)} = P (0, 1)+ P (1, 0) = q ·p+ p·q = 2p·q = 0, 48 .

К тому же результату придем и по определяющей формуле:

P (B = 1) = p₁= C₂1_p1_q1_{= 2}· p · q = 2pq = 0, 48.

Наконец, вероятность исхода (1, 1) вычисляется по правилу умноже-

ния независиых событий P (1, 1) = P (1) · P (1) = p · p = p²= 0, 36 или по

определяющей формуле P (B = 2) = p₂= C₂2_p2_q0_{= 1}· p²· 1 = p²= 0, 36 .

Полученный любым из двух рассмотренных способов ряд распределе-

ния, оформляют в виде таблицы биномиального распределения.

B

0

1

2

P p₀= q²= 0, 16 p₁= 2pq = 0, 48 p₂= p²= 0, 36

На Рис. 2 представлен полигон данного биномиального распределения

при значениях параметров n = 2 , p = 0, 6 .

45

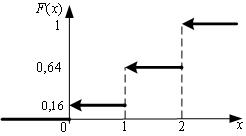
Рис. 2

Построим функцию биномиального распределения при n = 2 , p = 0, 6 .

По общему определению данная функция распределения должна возрастать

от нуля до единицы, имея скачки, равные 0, 16 , 0, 48 , 0, 36 в узлах 0 , 1 , 2 :





0,

x ≤ 0,

F (x) =



₀, 16, 0 < x ≤ 1,

 0, 64, 1 < x ≤ 2,





 1, x > 2.

На Рис. 3 представлен график данной функции распределения.

Рис. 3

Математическое ожидание данного распределения вычисляется в виде

m = np = 2 · 0, 6 = 1, 2 , а мода распределения находится по ряду распре-

деления в виде d = 1 . Характеристики рассеяния данного распределения

имеют следующие значения: дисперсия D = npq = 2 · 0, 6 · 0, 4 = 0, 48 и

стандартное отклонение σ =

√

npq =

√

0, 48 = 0, 69 .

Для вычисления вероятности попадания случаной величины на полу-

интервал [m − σ; m + σ) = [0, 51; 1, 89) можно применить два подхода.

46

Во-первых, воспользоваться формулой P (a ≤ B < b) = F (b) − F (a) и

уже найденной функцией распределения:

P (0, 51 ≤ B < 1, 89) = F (1, 89) − F (0, 51) = 0, 64 − 0, 16 = 0, 48.

Во-вторых, непосредственно подсчитать число значений случайной ве-

личины, которые попадают в указанный интервал, и суммировать соответ-

ствующие этим значениям вероятности: P (B = 1) = 0, 48 .