Классификация моделей

Модели

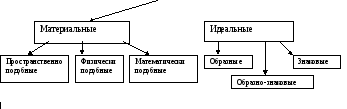
Схема 2.

Среди этих моделей выделяют:

- пространственно подобные модели – объекты, геометрически подобные своему прототипу;

- физически подобные модели – отражают подобие происходящих в них основных физических процессов, сходство их физической природы и тождественность законов движения;

- математически подобные модели – материальные системы, не обладающие с объектом одной и той же физической природой и не сохраняющие с ним физического или геометрического подобия, в которых происходят иные, чем в оригинале физические процессы. Здесь отношением между моделью и реальным объектом выступает аналогия. Эта аналогия может быть структурной и функциональной. Те и другие могут быть описаны одинаковыми или подобными математическими выражениями.

Идеальные, или абстрактные, концептуальные модели:

- образные модели – представляют собой образы каких-либо реальных, хорошо известных явлений, доступных непосредственному наблюдению, некоторые свойства и отношения моделируемых явлений представлены в этих моделях в форме, доступной чувственности, образные модели являются наглядными образами элементов, структуры и поведения объектов, они часто фиксируются в виде рисунка, чертежа, схемы;

- знаковые модели – отношения и свойства моделируемых явлений выражены при помощи определенных знаков; главная особенность таких моделей – полное и принципиальное отсутствие сходства между элементами модели и реального объекта; знаковая модель не обладает наглядностью в смысле сходства;

- образно-знаковые модели - сочетание образной и знаковой модели, занимающее промежуточное между ними положение.

Особое место занимает математическое моделирование и математическая модель.

Математика – наука о пространственных формах и количественных отношениях реального мира. Это некоторый универсальный язык, с помощью которого можно описать практически все явления окружающего мира, даже те, которые невозможно наблюдать непосредственно и трудно представить себе наглядно.

Математическим моделированием Вы начали заниматься уже в начальной школе, когда составляли простейшие математические выражения. Любое уравнение, неравенство, система, график – является математической моделью.

Пример.

Система линейных уравнений 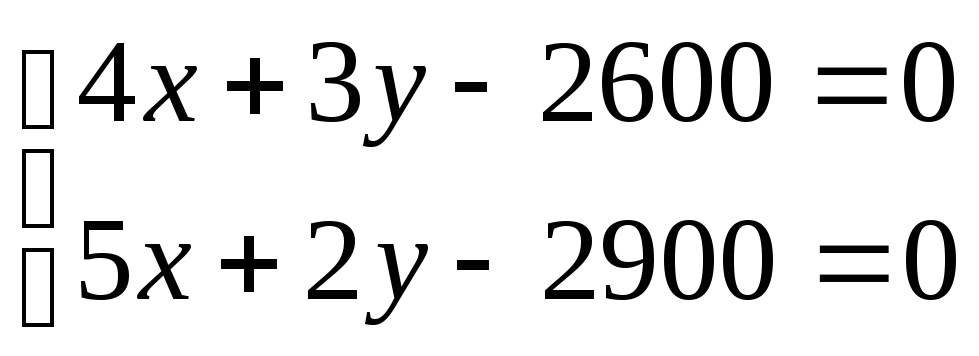может рассматриваться как математическая модель точки пресечения графиков двух линейных функций (прямых) на плоскости, или линии пересечения двух плоскостей, параллельных оси OZ в пространстве, или в экономике – являться моделью ситуации: «Предприятие выпускает два вида продукции, используя сырье двух типов. Необходимые характеристики производства указаны в таблице 4. (которая тоже является математической моделью данной ситуации)».

Таблица 5.

Вид сырья	Расход сырья по видам продукции, ед. вес./изд.		Запас сырья, ед. вес.
	Продукция А	Продукция В
1	4	3	2600
2	5	2	2900

В результате решения системы уравнений, получаем ответ на вопрос: Каков объем выпуска продукции каждого вида при заданных запасах сырья?

Графическая интерпретация системы уравнений приводит к возможности графического решения системы и интерпретации экономической ситуации.

Точного определения понятия математической модели не существует. Можно предложить описание характеристик математической модели (несколько десятков), весьма отличающихся друг от друга.

Полезная информация

Математическая модель – совокупность уравнений, неравенств, ограничений, математических формул, определяющих выходные свойства объекта в зависимости от входных свойств, параметров и начальных условий.

Математическая модель – математическая структура, объекты которой трактуются как реальные «вещи» (понятия), а абстрактные отношения между ними – как конкретные связи между отношениями действительности. При математическом моделировании сущность явлений выражается в знаках.

Математическая модель - приближенное описание какого-либо класса явлений внешнего мира, выраженного с помощью математической символики.

Математическая модель – система объектов или знаков, воспроизводящая некоторые существенные свойства системы-оригинала.

Иногда даже трудно определить, какая из двух сущностей является вещью, а какая – ее моделью (например, график функции и ее уравнение). При осуществлении выбора следует исходить из прагматических соображений: модель – это то, с чем проще работать, то есть легче увидеть, запомнить, передать, записать, исследовать…

Математическое моделирование предполагает построение действующей математической модели, которая обладает характеристиками или свойствами рассматриваемого объекта.

Результатом исследования этой модели оказывается прогнозирование поведения реального объекта.

Математическая модель глубже вскрывает внутренние связи объекта, дает его точные количественные характеристики.

Математическая модель занимает особое место среди моделей, используемых в науке, так как является формальной конструкцией, такие модели позволяют выделить «в чистом виде» логическую структуру научной теории и количественные отношения между существенными переменными изучаемых явлений. Это позволяет проверить логическую состоятельность содержательной теории, исследовать ее структуру и построить на ее основе количественно определяющие утверждения относительно связи между фактами, а следовательно, создается возможность для экспериментальной проверки теории и ее практического использования. Таким образом, математическое моделирование – один из наиболее экономичных, точных и эффективных методов теоретического анализа, обобщающего формулирования и экспериментально контролируемого описания объективных свойств и отношений реальности.

Математическое моделирование используется:

- для численного экспериментирования или численного оценивания в условиях, когда проведение реального эксперимента связано с большими затратами;

- для ознакомления, изучения и совершенствования новых объектов;

- для проверки или демонстрации новой идеи или метода;

- как средство планирования и прогнозирования.

Когда Вы начали изучать геометрию (планиметрию), Вы познакомились с геометрией Евклида - моделью окружающего нас мира, в которой все объекты состоят из простейших геометрических фигур: точек, прямых или их частей и плоскостей или их частей.

Требования к модели

С одной стороны, модель должна быть достаточно полной, то есть в ней должны быть учтены все факторы, от которых существенно зависит поведение исследуемого объекта.

С другой стороны, модель должна быть достаточно простой, чтобы возможно было установление зависимости между параметрами, входящими в нее.

В зависимости от математических понятий и методов, которые используются для моделирования изучаемых явления реальности, математические модели подразделяются на:

- функциональные;

- стохастические (вероятностные);

- алгоритмические;

- логико-математические;

- информационные;

- топологические.

Количество математических понятий, которое приходится использовать для описания модели некоторого явления может служить мерой сложности этого явления.

Цель моделирования (как математической деятельности) - выделение комплекса свойств, присущих данному объекту или явлению и описание их средствами математики.

Обычно модель записывается с помощью уравнений или неравенств. В результате изучения этих моделей часто возникают другие математические структуры.

Структура процесса математического моделирования.

1. Постановка задачи, определение целей моделирования (исследовательской задачи, решение которой и должно быть получено посредством использования модели) Примеры формулирования целей: получение сведений об устройстве конкретного объекта, его структуре, свойствах, законах развития и взаимодействия; управление объектом; прогнозирование воздействия на объект.

2. Ранжирование свойств объекта – разделение его свойств по степени важности и влияния. Создание (выбор) модели.

3. Исследование модели (опосредованное изучение моделируемого объекта).

4. Сопоставление полученных данных с данными об оригинале.

5. Перенос знания (правила перевода высказываний о модели в высказывания об оригинале). Здесь возможно появление ошибок.

Поясним каждый из выделенных этапов.

Пример.

Изучить многоквартирный жилой дом.

Таким образом сформулированная цель не позволяет определить ничего. Поскольку изучение объекта (в данном случае жилого дома) может проходить по нескольким, принципиально различным друг от друга направлениям. Например: 1) определить объем (площадь) жилых (служебных) помещений в этом доме; 2) определить количество краски, которое потребуется для окраски стен всех лестничных площадок; 3) Определить, можно ли построить такой же дом на соседнем пустыре, если известны размеры пустыря (пренебрегая особенностями грунта).

Заметим, что в первом случае существенными характеристиками объекта будут размеры квартир в этом доме. При этом предполагаем, что все квартиры, одинаково расположенные, имеют одни и те же размеры. Заметим, что, пренебрегая возможными отклонениями в размерах квартир одного типа, мы уже закладываем погрешность результата.

Во втором случае существенными характеристиками будут размеры лестничных клеток.

А в третьем случае – размеры основания жилого дома.

При составлении математической модели необходимо тщательно изучить само явление, установить характерные связи между величинами, его характеризующими, установить присущие ему основные свойства, которые следует учитывать при его изучении. Все это и определяет используемый математический аппарат исследования, точность описания, глубину соответствия модели изучаемому явлению.

Построение любой математической модели начинается с абстрагирования. Процесс абстрагирования в математике имеет свои характерные особенности, отличающие его от аналогичного процесса в других науках, поскольку способы абстрагирования зависят от природы изучаемых объектов, характера и целей их изучения.

После того как модель составлена и принята, начинается собственно составление математической схемы применения избранного моделью математического аппарата. Чисто логическим путем составляются различного рода уравнения между числовыми характеристиками явлений, выводятся следствия. Если оказывается, что имеющихся математических средств не хватает для описания модели, приходится разрабатывать новую математическую теорию.

Далее – проверка соответствия модели исследуемому явлению. Ее следует заменить на другую, более точную, если она плохо отражает качественную или количественную сторону описания изучаемого процесса.

Изучение явления природы или производственных, экономических, других процессов математическими методами осуществляется посредством промежуточного шага – составления сходного изучаемого явления или его математической модели.

Можно рассматривать более простую схему процесса математического моделирования, состоящую из трех этапов:

- формализация (запись соотношений между исследуемыми величинами в виде математических равенств или неравенств);

- математизация (исследование полученного математического объекта математическими средствами);

- интерпретация (формулировка полученного результата в терминах исходной задачи).

Наиболее часто встречающиеся в курсе математики стершей школы задачи, предполагающие осуществление математического моделирования – это задачи на оптимизацию.

Рассмотрим несколько таких задач с экономическим содержанием, а именно задач на определение оптимального выпуска продукции на конкурентном рынке, выделяя в ходе их решения этапы моделирования.

Задача 1.

Некоторая фирма работает на конкурентном рынке хлебобулочной продукции и занимается выпечкой пирожков. Функция издержек выпечки пирожков имеет вид: , где Q – количество пирожков (в тыс.шт.). Известно, что производственные мощности позволяют выпекать не более 2 тыс. пирожков в день. Определите, сколько пирожков в день следует выпекать этой фирме, чтобы получать максимальную прибыль, если рыночная цена пирожка составляет 8 руб. за штуку?

Для того чтобы успешно решить эту задачу, вспомним некоторые понятия экономики.

Прибыль P (profit) предприятия определяется как разность между общей выручкой (доходом), полученной от реализации продукции и общими издержками, связанными с затратами на ее производство и реализацию.

Поскольку выручка R (revenue) зависит от количества Q (quantity) единиц реализованной продукции, то она является функцией от количества, также как и затраты на производство и реализацию. Таким образом, можем записать следующее выражение для функции прибыли: P(Q)=R(Q)-S(Q).

Решение.

1 этап. Формализация.

Запишем выражение для функции прибыли в нашем случае: . Поскольку количество выпускаемых пирожков не может быть отрицательным и ограничено производственными мощностями фирмы, то задача сводится к исследованию построенной функции на экстремум (максимум) на отрезке .

2 этап. Математизация.

Найдем производную данной функции: . Найдем нули найденной производной. Для этого решим уравнение: или

Решениями данного уравнения являются числа -4 и 1, первое из которых не удовлетворяет условию задачи. Теперь осталось убедиться в том, что в точке Q=1 находится максимум данной функции. Для этого можно использовать разные способы.

1) Один из них – просто посчитать значения функции на концах отрезка и в найденной стационарной точке. ; ; . Видно, что полученная точка действительно является точкой максимума.

2) Для определения того факта, что найденная точка на самом деле является точкой максимума, можно воспользоваться следующими соображениями. На отрезке функция имеет единственную стационарную точку. Квадратичная функция , имея отрицательный коэффициент при старшем члене, при переходе через свой правый корень меняет знак с плюса на минус (слева направо). Таким образом, справа от точки Q=1 производная имеет знак «+», значит функция возрастает, а слева от этой точки производная имеет знак « - » и функция убывает. Таким образом, точка Q=1является единственной точкой экстремума на рассматриваемом отрезке о она точка максимума. Значит в этой точке функция имеет наибольшее значение на данном отрезке.

3 этап. Интерпретация.

Фирме следует выпекать 1 тыс. штук пирожков ежедневно, чтобы получать максимальную прибыль.

Кроме того, вычислив значение функции в точке Q=2 мы получили отрицательный результат, который можно проинтерпретировать следующим образом: работая на полную мощность, фирма будет терпеть издержки. Можно исследовать построенную функцию для выяснения вопроса: когда производство перестанет приносить прибыль? Для этого достаточно найти нули функции.

Задача 2.

Допустим, что все затраты фирмы определяются только расходами на оплату труда работников. Будем считать, что все остальные ресурсы не влияют на затраты фирмы. Еженедельный выпуск продукции зависит от количества нанятых рабочих следующим образом: . Недельная ставка нанятого рабочего составляет 80$. Производимый товар фирма реализует на конкурентном рынке по цене 10$ за единицу товара. Если фирма нанимает работников на конкурентном рынке труда, то сколько работников нужно нанять владельцу фирмы, чтобы получить максимальную прибыль?. Какое количество продукции произведут эти работники за неделю?

Решение

1 этап. Формализация.

Поскольку в данной задаче все издержки фирмы определяются только затратами на оплату труда рабочих, то общие издержки будут определяться формулой: S(L)=80L. Выражение для функции прибыли будет иметь вид: .

2 этап. Математизация.

Исследуем полученную функцию на наибольшее значение. Поскольку функция квадратичная с отрицательным старшим коэффициентом, то наибольшего своего значения она достигает при . При этом значении .

3 этап. Интерпретация.

Владельцу фирмы следует нанять 94 работника, которые за неделю будут производить 353440 ед. продукции.

Задачи для решения

1. Вспомните или найдите примеры моделей, используемые в различных науках.

2. Ответьте на следующие вопросы.

1) Как вы думаете, от чего зависит сложность математической модели?

2) Приведите примеры математических моделей физических, химических, биологических процессов и явлений.

3. Решите задачу.

Николай Кузьмич выращивает огурцы на своем приусадебном участке. Затем весь свой урожай он продает на городском конкурентном рынке. Известно, что рыночная цена на огурцы составляет 20 руб. за кг. Зависимость общих затрат на выращивание огурцов от их количества определяется функцией:.

Сколько килограммов огурцов нужно вырастить Николаю Кузьмичу, чтобы получить при их продаже максимальную прибыль?

Постройте график функции прибыли от количества выращенных огурцов. Найдите те значения Q, при которых прибыль становится равной нулю, отрицательной.

Занятие 4.2. Функция как математическая модель

Основное содержание

Функция. Понятие. Способы задания. Свойства функций. Процессы и явления, описываемые с помощью функций. График функции как модель процесса и явления. Интерпретация результатов исследования функции в соответствии с условиями задачи.

Приведем фрагмент содержания занятия.

Функция является одним из важнейших понятий в математике. И как один из основных инструментов используется в других науках для изучения различных процессов, природа которых может быть различной, но математическая модель – функция – оказывается одинаковой.

Основные задачи, связанные с понятием «функция», которые решаются в школе:

• математическая задача (описание свойств функции на основании формулы или на основании графика, построение графика и т.д.)

• прикладная задача, решение которой состоит из нескольких этапов:

- конструирование функции по сюжету;

- исследование построенной функции (решение математической задачи);

- интерпретация полученного результата

В качестве примеров прикладных задач, решаемых в школе, можно привести задачи на наибольшее или наименьшее значение.

Напомним, что термин «функция» был введен Лейбницем, а символьная запись - Леонардом Эйлером.

Сформулируем несколько определения понятия функция, взятые из школьных и вузовских учебников.

Определение 1. Если каждому значению х из некоторого множества чисел Х поставлено в соответствие единственное число у, то говорят, что на этом множестве задана функция у(х). При этом х называют независимой переменной, а у – зависимой переменной или функцией.

Определение 2. Говорят, что переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого х однозначно определить значение у.

Определение 3. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу единственное число у, зависящее от х.

Определение 4. Функцией f(x) называется правило, которое каждому элементу х из множества Х ставит в соответствие единственный элемент у из У.

Заметим, что когда множество Х – числовое множество, речь идет о функции числового аргумента, когда У – числовое множество, то речь идет о числовой функции, когда оба эти множества числовые, то речь идет о числовой функции числового аргумента.

Независимо от того, какое определение функции мы используем, необходимо помнить, что принципиальным является возможность существования не более одного значения зависимой величины. Поэтому, например, уравнение не задает функцию : каждому положительному значению х ставится в соответствие два противоположных значения у. Но оно задает функцию : каждому значению у как независимой переменной ставиться в соответствие ровно одно значение х как зависимой переменной. Таким образом, мы видим, что без уточнения, о какой зависимости идет речь, какая переменная рассматривается как зависимая, а какая как независимая, мы не можем говорить о том, задана функция или нет.

Теперь напомним известные способы задания функций.

• табличный (нельзя задать непрерывную функцию, неограниченную функцию)

• словесный (описанием)

• аналитический (с помощью формулы). Здесь можно выделить:

- явное задание функции;

- неявное задание функции (в том числе параметрическое);

- кусочно-заданные функции

• графический (с помощью графика) тоже не позволяет задать неограниченную функцию или функцию на неограниченной области определения.

Полезная информация

Неявное задание функции. Наряду с уравнением вида мы можем задать функцию с помощью уравнения . Если изменяется значение переменно х, то изменяется и значение переменной у. Например: уравнение задает функцию . В этом случае переменную у можно явно выразить через х. Однако так бывает не всегда. Часто выразить переменную у через х бывает затруднительно и даже невозможно: .

Параметрическое задание функции. Функция может быть задана с помощью системы уравнений, содержащих некоторый промежуточный параметр: 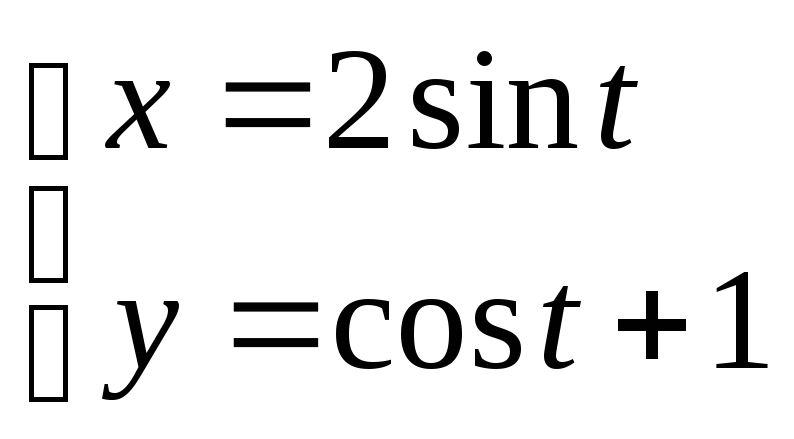. Если изменяется переменная х, то изменяется значение параметра t, а это влечет за собой изменение переменной у.

К основным элементарным функциям относятся: степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.

Все функции, которые получены из основных элементарных с помощью конечного числа арифметических действий (сложения, вычитания, умножения и деления) и композиций тоже являются элементарными.

Напомним основные свойства функций.

1. Область определения (область задания) функции.

2. Множество значений (область значений) функции.

Если мы выбираем определение понятия функции, как переменной величины и рассматриваем зависимость, например, переменной у от переменной х, то множество значений, которые может принимать переменная х, называется областью определения функции у(х), а множество значений, которые может принимать переменная у, называется множеством значения этой функции.

Рассмотрим несколько примеров.

Пример.

Найдите область определения функции, заданной аналитически.

1) .

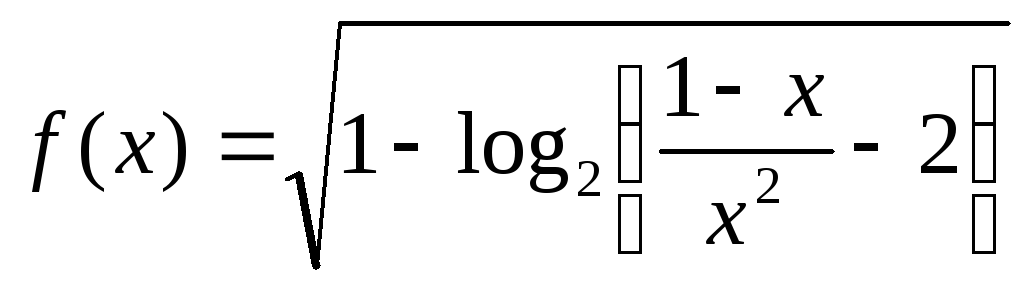2) .

Решение

1. Обратим внимание на те ограничение, которые формируют область определения данной функции. Во-первых, выражение содержит корень четной степени, поэтому выражение, стоящее под знаком корня, должно быть неотрицательным. Во-вторых, выражение содержит логарифм, поэтому выражение, стоящее под знаком логарифма, должно быть положительным. В-третьих, решая неравенство для функции, стоящей под знаком логарифма, нельзя забыть о знаменателе, который не должен равняться нулю. Таким образом, получаем систему ограничений:

, которую и решаем. Результат решения этой системы и является областью определения данной функции.

2. Для того чтобы найти область определения второй функции, вспомним, что функция арккосинус определена на отрезке 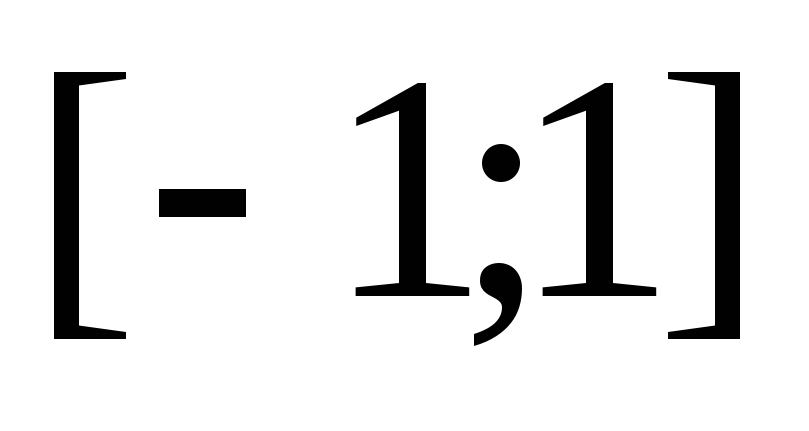. Кроме того, выражение содержит корень четной степени, поэтому подкоренное выражение должно быть неотрицательным. Получаем систему ограничений: , которая и ограничивает область определения данной функции.

Пример.

Функция задана уравнением: . О какой функции идет речь. Выразите зависимую переменную и найдите область определения и множество значений этой функции.

Решение

Очевидно, во-первых, что функция, предложенная в данном примере, задана неявно. Поскольку ни одна из переменных не выражена явным образом.

Во-вторых, проанализировав выражение, мы увидим, что для каждого значения можно найти два значения для переменной у, что не позволяет говорить о функции у(х).

Таким образом, попробуем рассмотреть функцию х(у): . Видно, что эта функция определена для всех значений переменной у. То есть область определения этой функции – все множество действительных чисел. Множество значений этой функции - интервал .

3. Корни (нули) функции.

Определение. Число из области определения функции y=f(x) называется нулем (или корнем) этой функции, если f(x₀)=0.

Таким образом, для нахождения нулей функции необходимо решить уравнение f(x₀)=0.

Пример.

Найдите нули функции.

1) ;

2) .

Решение

1) Поиск корней данной функции можно начать с поиска области ее определения, но можно сначала решить соответствующее уравнение и проверить найденные корни. Так и поступим.

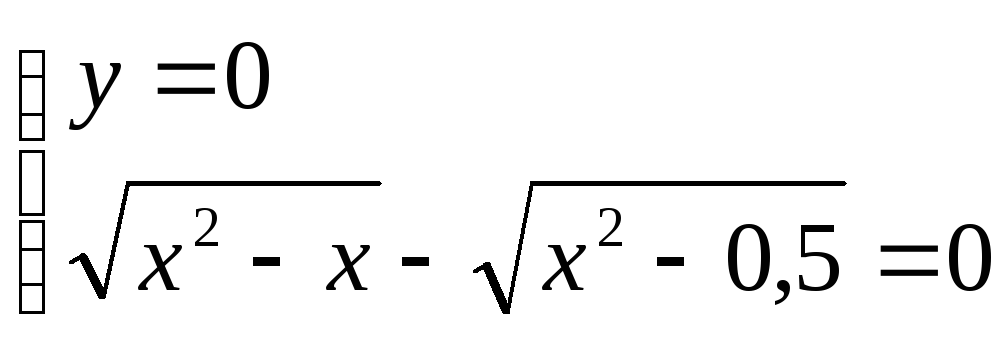. Решим второе уравнение: . Возводя обе части этого уравнения в квадрат (это приводит к уравнению, равносильному на ОДЗ данного уравнения), получаем: или х=0,5. Теперь нужно проверить, удовлетворяет ли полученное решение области определения нашей функции. Простая проверка показывает, что при х=0,5 выражение под знаком первого корня меньше нуля и поэтому найденное нами число не принадлежит области определения. Вывод, который мы получили: данная функция нулей не имеет.

2) Вторая функция задана неявно. В этом случае мы можем подставить у=0 в данное уравнение и решить его относительно х: , или (*). Используя известные Вам методы решения логарифмических уравнений, получаем: , или 2х+1=х, решением которого является число х=-1. Поскольку областью определения уравнения (*) является любое действительное число, то найденное значение х нас устраивает. Вывод. Функция обращается в 0 при х=-1.

4. Промежутки знакопостоянства. Промежутки, на которых функция сохраняет знак.

Заметим, что поиск промежутков знакопостоянства, как правило, сводится к поиску точек, в которых функция меняет свой знак (как правило, это ее нули и границы области определения), и расстановке знаков на найденных промежутках с помощью метода интервалов. В некоторых случаях можно воспользоваться некоторыми известными свойствами функций. Это особенно полезно, когда речь идет о сложных функциях.

Пример.

Найдите промежутки знакопостоянства функции:

1) ;

2)

Решение

1. К выполнению данного задания можно подойти двумя разными способами.

   1. Для определения промежутков знакопостоянства найдем нули нашей функции, а для этого решим уравнение: 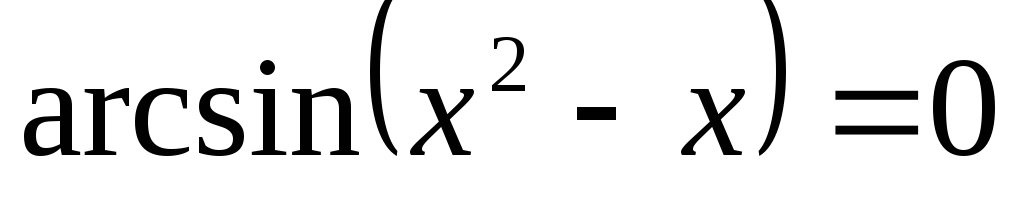, или . Его решениями являются числа х=0 и х=1. Они разбивают числовую прямую на три промежутка: . При х=-1 получаем: . Таким образом, на самом левом промежутке функция имеет знак «+». 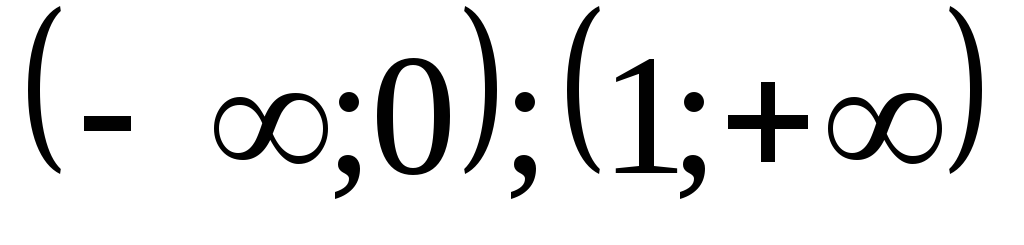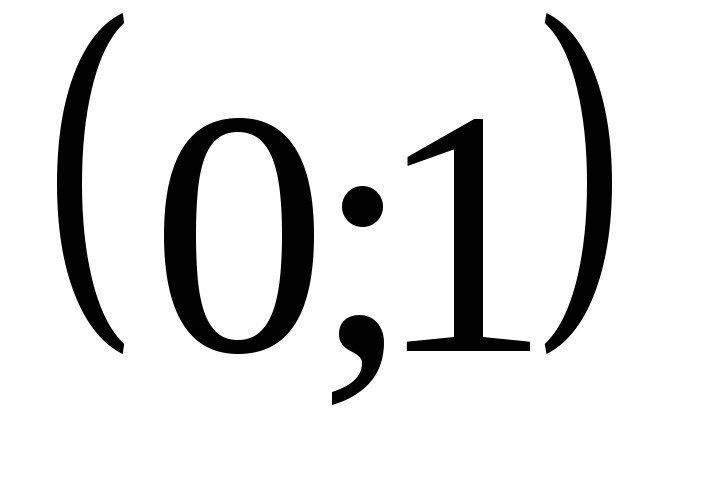Учитывая чередование знаков, получаем три промежутка знакопостоянства: , на которых функция положительна, и , на котором функция отрицательна. Но для окончательного решения необходимо найти область определения функции. Она, как вам известно, определяется двойным неравенством: 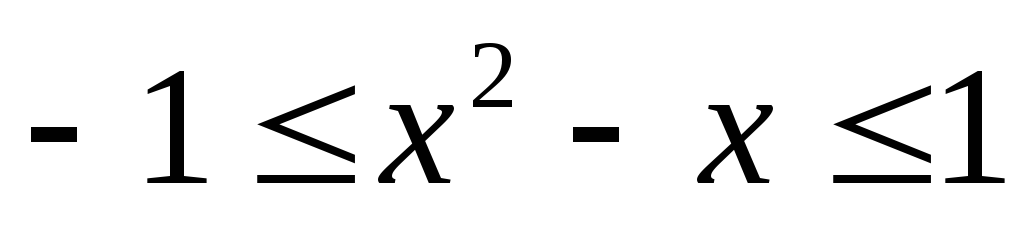, решая которое получаем: 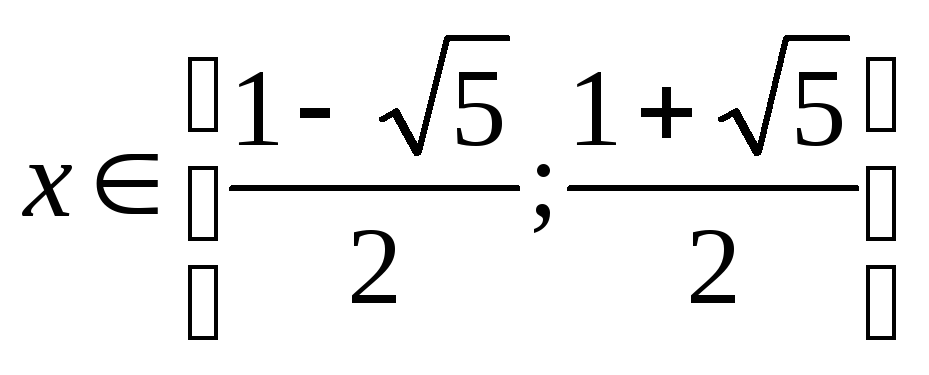. И промежутки знакопостоянства выглядят следующим образом: 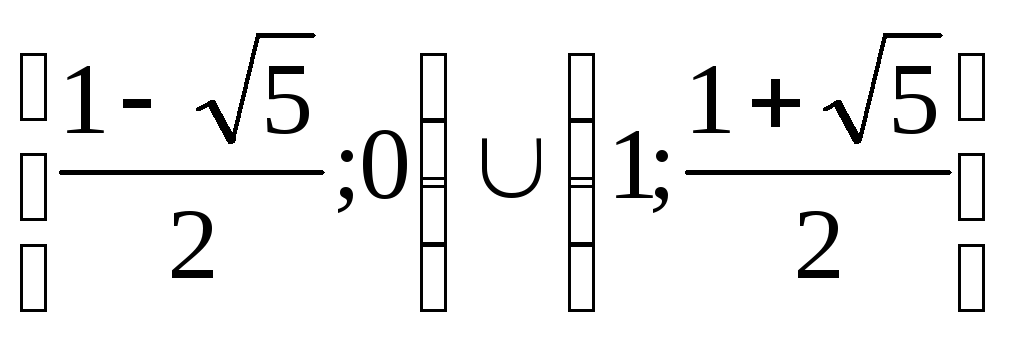функция положительна и 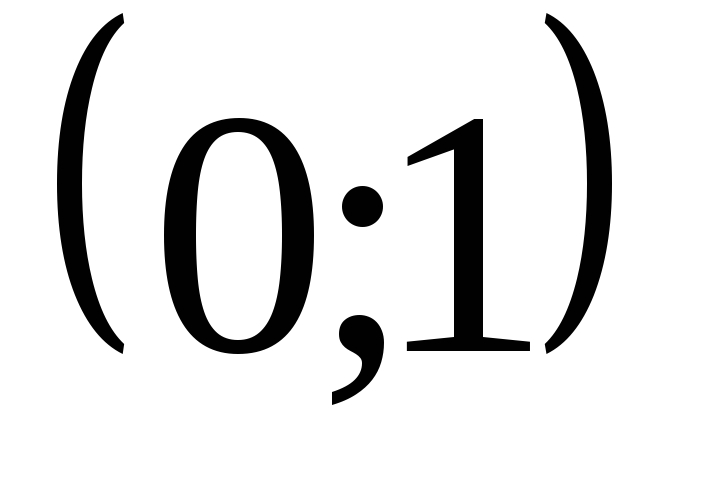, на котором функция отрицательна.

   2. Знак функции 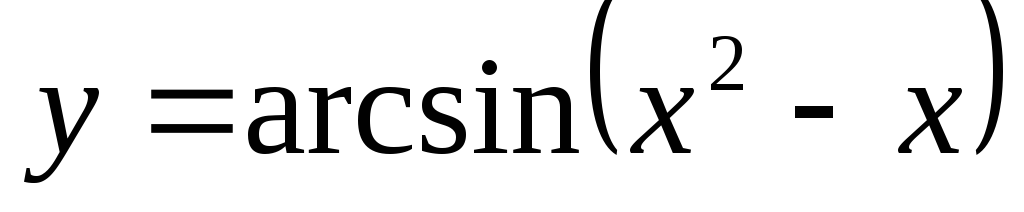определяется знаком выражения 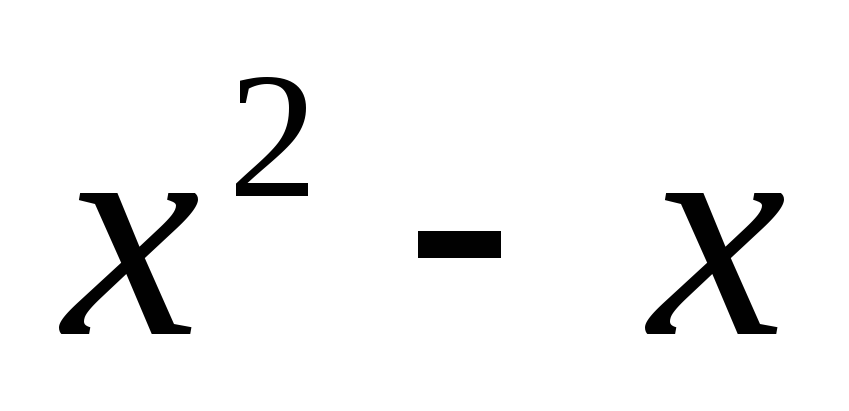, поскольку знак функции арксинус совпадает со знаком ее аргумента. Поэтому для ответа на вопрос задачи требуется определить промежутки знакопостоянства функции на отрезке .

2) Знак функции зависит от знаков и числителя, и знаменателя. Поэтому нужно найти точки, при которых происходит изменение их знаков. Для этого решим уравнения: . Решением второго уравнения является число х=4. Решая первое уравнение, получаем: , или , решением которого являются числа х=-1 и х=3. Число х=-1 не является решением исходного уравнения и это значит, что данная функция не изменяет знак в точке х=-1. Поэтому найденные две точки разбивают числовую прямую на три промежутка: . Теперь для определения знака подставим, например, число х=0. При этом значении наша функция отрицательна. Дальше ее знак изменяется в точке х=3 (с «-» на «+») и в точке х=4 (с «+» на «-»). Учитывая область определения данной функции: , получаем окончательный ответ: при функция отрицательна и при функция положительна.

5. Четность или нечетность функции.

Определение. Функция f(x) называется четной (нечетной), если для любого значения х независимой переменной из области определения функции выполняется равенство: f(-x)=f(x) (f(-x)=-f(x)). Из этого определения следует, что необходимым условием четности или нечетности функции является симметричность ее области определения относительно нуля!

6. Периодичность.

Определение. Функция f(x) называется периодической, если существует такое число Т, что для любого значения х независимой переменной из области определения функции выполняется равенство: f(x+T)=f(x).

7. Монотонность.

Определение. Функция f(x) называется монотонно возрастающей (убывающей) на промежутке , если для любой пары значений х₁ и x₂ независимых переменных из этого промежутка выполняется следствие: ().

8. Экстремумы.

Определение. Точка х₀ из области определения функции называется точкой максимума (минимума) этой функции, если существует такая окрестность этой точки, что для любого выполняется неравенство: ().

9. График функции. Определение. Графиком функции называется множество точек плоскости с координатами , где .

Линейная функция служит основой большого количества математических моделей, которые позволяют исследовать многие реальные процессы. Было бы неправильно утверждать, что все эти процессы линейны. Просто для эффективного их изучения достаточно линейного приближения.

Рассмотрим простейший пример.

Задача 1.

Затраты на перевозку одного и того же груза разными видами транспорта определяются формулами:

;

, где х – расстояние в километрах, - стоимость перевозки в рублях. Постройте графики этих функций. На каких расстояниях выгодно пользоваться первым видом транспорта? Начиная с какого расстояния экономичнее становится второй вид транспорта?

Решение

Напомним, что для построения графика линейной функции достаточно двух точек на плоскости. (Из геометрии: через две точки проходит прямая и притом только одна, что означает, что прямая однозначно определяется двумя точками). Поэтому предполагаем, что с первой частью задания вы справитесь самостоятельно. Сделаем лишь два замечания:

1) Очевидно, что областью определения линейной функции является все множество действительных чисел. Однако, как уже говорилось выше, в первой части этого урока, на практике известные функции рассматриваются не на естественной, а на искусственной области определения, которая часто определяется соображениями здравого смысла. В нашем случае такой областью определения является только множество положительных чисел (расстояние не может быть выражено отрицательным числом). Таким образом, график будет располагаться только в первой координатной четверти.

2) Для того чтобы максимально эффективно расположить и показать график любой функции нужно правильно выбрать масштаб. Поскольку свободный коэффициент наших функций значителен, целесообразно в качестве единичного отрезка на оси ординат выбрать две клетки, каждая из которых равна 500 единицам стоимости перевозки. Единичный отрезок по оси ординат также может быть выбран, равный двум клеткам, в каждой из которых содержится 500 км.

Ответить на вопросы задачи с помощью графиков достаточно просто. Напомним, что значения одной из функций меньше на тех промежутках области определения, где график ее расположен ниже. Поэтому использование первого вида транспорта будет выгоднее до тех пор, пока график первой функции будет располагаться ниже графика второй функции, то есть до того момента, пока они не пересекутся.

Однако для ответа на вопросы задачи необязательно строить графики функций. Достаточно найти решение неравенства: 1500+3х<3000+1,5х (значения первой функции меньше, чем значения второй). Решением этого неравенства является x<1000. Что означает: первым видом транспорта выгоднее пользоваться, когда расстояние перевозок не превышает 1000 километров. Дальше выгоднее пользоваться вторым видом транспорта. На 1000 км везти груз можно любым видом транспорта. Затраты будут одинаковыми.

Теперь рассмотрим применение линейной функции к решению задач оптимизации.

Задача 2.

Расстояние между двумя шахтами А и В по шоссейной дороге 60 км. На шахте А добывают 200 т руды в сутки, а на шахте В – 100 т руды в сутки. Где нужно построить завод по переработке руды, чтобы для ее перевозки количество тонно-километров было наименьшим?

Решение

Под тонно-километрами понимается количество тонн руды (к), перевезенное на определенное количество километров (у). Таким образом, количество тонно-километров равно произведению ку.

Предположим:

1) Завод строится на шоссе, в некоторой точке С. То есть сумма расстояний АС+ВС=60.

2) Все количество руды, добытое в шахтах, подлежит переработке на этом заводе.

Очевидно, что суммарное количество тонно-километров зависит от расположения завода на шоссе.

Обозначив расстояние АС=х, получим формулу, выражающую количество тонно-километров: 200х+100(60-х)=100х+6000. Таким образом, мы получили функцию зависимости количества тонно-километров от удаленности завода от шахты А.

Полученная функция является монотонно возрастающей и определена на отрезке [0;60]. Поэтому наименьшее свое значение она принимает на левом конце области определения, то есть при х=0. Значит, наименьшее количество тонно-километров равно 6000. Завод нужно строить около шахты А.

Еще одним важным аспектом использование функций как математических моделей – использование функций, заданных с помощью таблиц.

Очевидно, с помощью таблицы, как уже отмечалось во второй части нашего урока, можно задать только дискретную функцию. Мало того, в таблице обычно указан набор значений в фиксированных точках с выбранной точностью.

Например, в таблице задана функция, .

х	1	1,5	2	2,5
у	1,3	1,8	2,5	4

Если требуется определить значение функции в точке х, равной, например 1,25, приходится прибегать к интерполированию, то есть к приближенному нахождению неизвестных значений функции по ее известным значениям.

Наиболее простым является случай линейного интерполирования, то есть приближения неизвестной функции линейной.

Допустим, что в результате изучения некоторого явления и произведенных измерений получены значения некоторого параметра р, которые отражены на графике в виде точек с координатами . Все эти точки почти ложатся на прямую (рис. 18.). Это значит, что, допуская некоторую погрешность, можно считать, что зависимость p(t) – линейная.

Рис. 18.

Пусть известно значения функции y=f(x) и в точках и соответственно. Предполагаем, что между этими точками функция примерно совпадает с линейной, имеющей такие же значения. Уравнение линейной функции выглядит следующим образом: , где . Таким образом, считают, что на промежутке значения функции - интерполяционная формула. Величина называется интерполяционная поправка и вычисляется с помощью дополнительной таблицы.

Если по заданным значениям функции нужно найти приближенной значение аргумента, то используют обратное интерполирование.

Приведем пример.

Задача.

Пусть функция y=f(x) задана таблицей:

х	1	1,05	1,1	1,15
у	1,35	1,85	2,55	4,45

Используя линейное интерполирование, найти f(1, 055).

Решение

Имеем: =1,85 и =2,55 в точках =1,05 и =1,1 соответственно.

=1,1-1,05=0,05 и =2,55-1,85=0,7. Подставим найденные величины в интерполяционную формулу и получим:

. Подставив в эту формулу значение х=1,055, получим приближенное значение функции: f(1,055)=1,85+14(1,055-1,05)=1,85+0,07=1,92.

Если точность нахождения неизвестных значений функции с помощью линейного интерполирования по каким-то причинам не устраивает, оказывается недостаточной, то используются другие методы интерполирования, например, квадратичное интерполирование.

Задачи для решения

1. Из функций, заданных с помощью таблицы, выберите ту, которая удовлетворяет данному уравнению, и закончите таблицу.

.

1)

х	1	2	3	4	5	6	7	8	9
у	2	5	8	15

2)

х	1	2	3	4	5	6	7	8	9
у	2	5	10	17

3)

х	1	2	3	4	5	6	7	8	9
у	2	5	10	13

2. Выберите формулы, которые задает функцию у(х):

1) ;

2) ;

3) ;

4) (+);

5) ;

6) .

3. Решите задачу 2., изменив условие. а) В шахте А добывалось 100 т, в шахте В – 200 т., б) В шахтах А и В добывалось по 200 т.

4. Расстояние между заводами А и В равно 40 км. Потребность завода А составляет 80 т нефти в сутки, а завода В – 70 т в сутки. Перевозка одной тонны нефти на расстояние 1 км для завода А стоит 8 руб., а для завода В – 10 руб.. Где нужно строить нефтебазу для обеспечения заводов А и В горючим, чтобы расходы на перевозку были наименьшими?

5. Пусть функция y=f(x) задана таблицей:

х	1	1,05	1,1	1,15
у	1,35	1,85	2,55	4,45

а) Используя линейное интерполирование, найти f(1, 155).

б) Используя обратное интерполирование, найдите значение х, при котором f(x)=4.

Занятие 4.3. Уравнения и неравенства как математические модели

Основное содержание.

Понятие уравнения и неравенства. Уравнения и неравенства как математические модели. Интерпретация результатов решения уравнений и неравенств.