Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції

Кінець попереднього розділу наводить на думку, що можливо і означення похідної функції з дійсного аналізу теж можна перенести на комплексні функції. Далі буде розглянута така можливість.

§1 Похідна функції комплексної змінної. Критерій її існування

Простий аналіз означення похідної з дійсного аналізу показує, що воно може бути перенесене на функції комплексного аргументу.

Означення. Нехай функція задана в деякому околі точки . Якщо існує границя , то її ми називатимемо похідною функції в точці і позначатимемо .

Приклад 1. Розглянемо функцію на предмет існування від неї похідної в точці . Обчислимо таку границю:

.

Отже, для .

Приклад 2. Нехай тепер і . Розглянемо

.

Що стосується останньої границі, то вона не існує ні при жодному . Тому функція не має похідної в жодній точці комплексної площини.

Звернемо увагу, що вище ми привели означення похідної для функції , яка задається в деякому цілому околі точки . Проте це означення буде коректним, якщо ця функція буде задана на деякій множині , для якої точка є граничною. В цьому випадку похідну записуватимемо так

.

Приклад 3. Нехай маємо функцію , яка задана на множині дійсних чисел. Тут існує завжди і дорівнює 1 на всій множині. Поширимо цю функцію на всю комплексну площину , , де .

З’ясуємо чи має ця функція похідну в

.

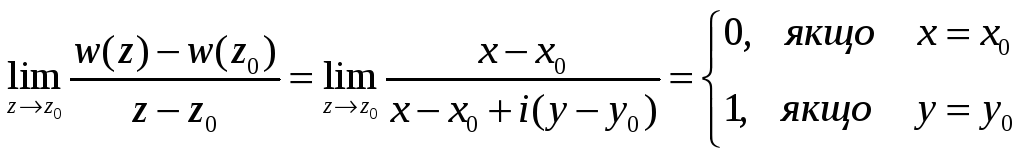Це означає, що такої границі нема в жодній точці і тому наша функція не має похідної в жодній точці комплексної площини.

Ці два приклади показують, що існування чи не існування похідної функції комплексного аргументу суттєво залежить від множини, по якій вона шукається.

Зауважимо, що якщо ми вимагаємо від функції комплексного аргументу існування похідної в деякій точці (по всій множині комплексних чисел), то ми тим самим ставимо для функції значно більш жорстку вимогу, ніж при аналогічній постановці для функції на дійсній прямій, бо в цьому випадку ми практично вимагаємо існування відповідної границі вздовж довільного напрямку прямування до (та ще й щоб ці границі по будь-якому напрямку були рівні), на відміну від дійсної прямої, де цей напрям практично один (сама пряма). В зв’язку з цим можна чекати від диференційованої функції комплексного аргументу властивостей, яких не має її дійсний аналог. Далі ми переконаємося втому, що таке має місце.

Незважаючи на зауваження, зроблені вище, означення похідної функції комплексного аргументу формально ідентичне до того означення, що було в дійсному аналізі. А це означає, що всі правила диференціювання, які були там, аналогічним способом переносяться і на комплексний аналіз (похідна суми, добутку, частки, складної і оберненої функції).

Приклад функції , дійсна частина якої , коефіцієнт при уявній частині якої , незважаючи на чудові диференціальні властивості останніх показує, що для існування похідної функції комплексного аргументу мало таких властивостей функцій і , а потрібне ще щось. Що саме, показує наступне твердження.

Нехай − функція, задана в деякій комплексній області .

Теорема. (Критерій диференційовності)

Для того, щоб функція , задана в області , була диференційовною в точці необхідно достатньо, щоб

1. функції і 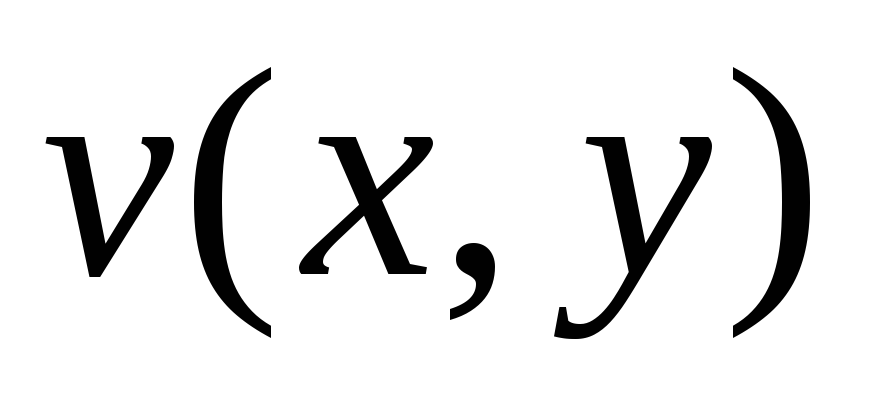як функції двох дійсних змінних були диференційованими в точці ;

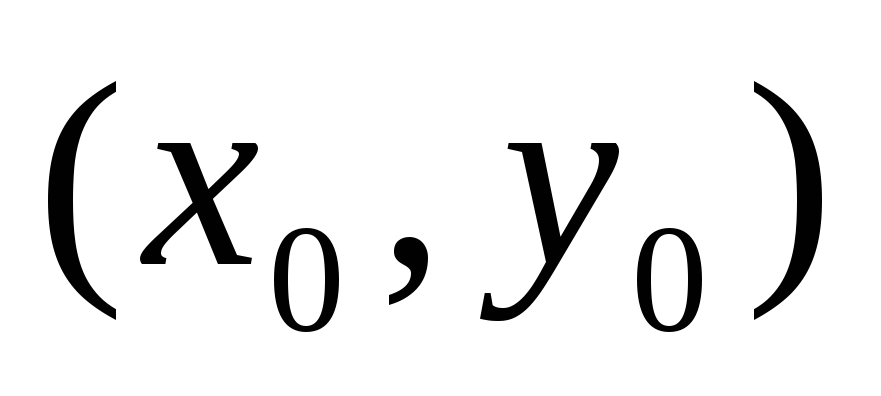2. в цій точці були справедливі рівності

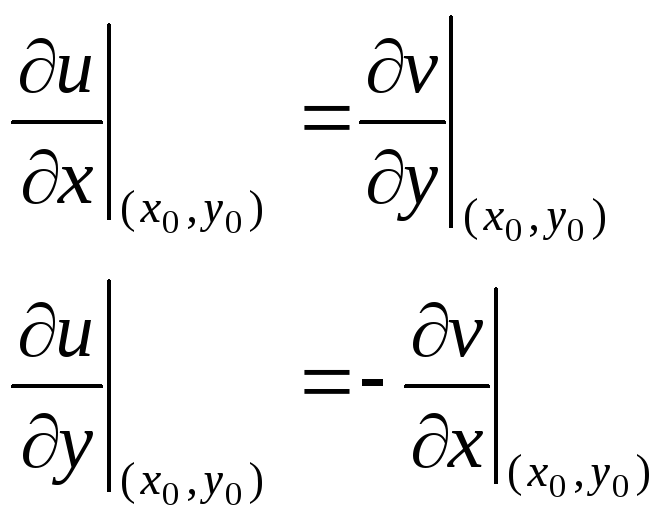(1)

Ці рівності називають умовами Коші-Рімана.