Доведення

Необхідність. Нехай точка полюс кратності функції . Тоді точка буде нулем кратності для функції . З аналітичності функції і з вище сказаного будемо мати, що в кільці ,

, .

Тоді,

.

І оскільки функція аналітична, то

, .

Достатність. Нехай розклад функції в ряд Лорана в околі точки має вигляд

, .

Покажемо, що точка є нулем кратності для функції .

.

В чисельнику останньої рівності стоїть аналітична в деякому околі точки функція, яка в цій точці в 0 не перетворюється. Звідси для функції будемо мати:

,

причому дріб справа є аналітичною в деякому околі точки функція і тому будемо мати,

, .

З останньої рівності видно, що точка є нулем кратності для функції , а отже, вона є полюсом цієї ж кратності для функції . Теорема доведена.

Нам залишилося ввести ще одну особливу точку.

Означення 3. Точка називається істотньо особливою точкою, аналітичної в деякому проколеному околі точки , функції , якщо не існує ні скінченої, ні нескінченної .

Оскільки ізольованих особливих точок може бути лише три види, то вже зараз можна сказати що

Для того, щоб точка була істотньо особливою точкою для функції необхідно і достатньо, щоб її розклад в ряд Лорана в області містив безліч членів з від’ємними степенями (або безліч коефіцієнтів були рівні 0).

Наступне дуже важливе твердження характеризує поведінку функції в околі істотньо особливої точки

Теорема. (Сохоцький)

Якщо є істотньо особливою точкою функції, то для (в тому числі і ) існує послідовність збіжна до точки : , коли .

Доведення

З того, що функція необмежена в деякому околі точки випливає, що існує послідовність , яка збіжна до точки і . Випадок, коли , доведений. Нехай . Припустимо, що висновок цієї теореми для цього невірний. Для того, щоб записати його на мові , напишемо, що означає висновок цієї теореми для числа

, : : .

Звідси, заперечивши це твердження, будемо мати:

, , : . Розглянемо функцію в . Як видно із співвідношення (1) ця функція тут є обмеженою і значить для неї ця точка є правильною, а отже, існує (0 тому, що функція є необмеженою в цьому околі). Звідси випливає, що точка є для функції нулем. Тоді для функції , а значить і для , ця точка є полюсом, але ж вона за умовою теореми є для функції істотно особливою точкою. Отже, наше припущення невірне, а значить справедливий висновок цієї теореми. Теорема доведена.

З теореми випливає, що множина значень, аналітичної в деякому околі істотно особливої точки, функції є така, що її замикання (множина в об’єднанні з множиною граничних точок) співпадає зі всією розширеною комплексною площиною.

Якщо ми розглянемо функції і , то неважко показати, що точка буде істотно особливою для цих функцій. Легко показати, що існують послідовності, які збіжні до 0 такі, що послідовності значень обох цих функцій будуть збіжними до . Для другої функції існує послідовність, яка збіжна до 0, така, що послідовність значень цієї функції в точках даної послідовності буде збіжною до 0. Що стосується інших значень (а для 1-ї функції і ), то існують послідовності, які збіжні до 0: послідовності значень обох цих функцій не те що збігаються до , а є стаціонарними і кожний її член дорівнює числу . Виявляється, що таку властивість мають не тільки ці дві функції.

Означення. Точка називається - точкою функції , якщо .

Справедлива наступна

Теорема. (Велика теорема Пікара)

Нехай − деяка функція, яка аналітична в деякому околі точки і ця точка є для неї істотно особливою точкою. Тоді для , за винятком хіба що ще одного значення , існує послідовність - точок функції , яка збіжна до точки .

З цієї теореми випливає, що множина значень, які приймає аналітична в достатньо малому околі істотно особливої точки функція, є вся площина, за винятком можливо однієї точки. Це виключення не залежить від розміру околу, а залежить від природи функції. Для функції таким виключним значенням є точка 0, для функції його немає.

Простий аналіз вигляду рядів Лорана для функцій аналітичних в околах різних особливих точок показує, що головну роль при цьому відіграє та частина ряду Лорана, яка розміщена по від’ємних степенях . Через це, якщо точка - скінченна особлива точка, то частина ряду Лорана, розміщена по від’ємних степенях називається головною частиною ряду, а інша частина (по невід’ємних степенях ) – правильною.

Нехай – функція аналітична в деякому околі нескінченно віддаленої точки (). Тоді для того, щоб з’ясувати якою особливою точкою буде нескінченно віддалена точка, потрібно розглянути відображення , яке окіл нескінченно віддаленої точки переведе в деякий окіл точки 0 і замість функції одержимо функцію

.

Отже, все буде залежати від того, якою є точка 0 для функції . Можливі 3 варіанти:

1. точка 0 є для функції усувною особливою точкою, тоді розклад цієї функції в ряд Лорана буде мати вигляд:

;

2. точка 0 є для функції полюсом кратності 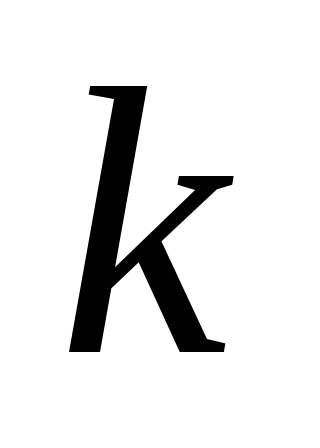, тоді розклад цієї функції в ряд Лорана буде мати вигляд:

, ;

3. точка 0 є для функції істотно особливою точкою, тоді розклад цієї функції в ряд Лорана буде мати вигляд:

.

Тоді відповідно в першому випадку нескінченно віддалену точку називатимемо правильною для функції і її розклад в ряд Лорана в області буде мати вигляд,

.

В другому випадку нескінченно віддалену точку називатимемо полюсом кратності для функції і її розклад в ряд Лорана в буде мати вигляд,

, .

В 3-му випадку нескінченно віддалену точку називатимемо істотно особливою точкою для функції і її розклад в ряд Лорана в буде мати вигляд:

.

Простий аналіз всіх цих 3-ох ситуацій показує, що у випадку нескінченно віддаленої точки головною частиною ряду Лорана є та його частина, яка розміщена по натуральних степенях, а правильною – по недодатних.

Закінчимо цю частину такою інформацією. З самого вигляду ряду Лорана по степенях, наприклад, без інформації, де цей ряд збіжний не можна зробити висновок якою особливою точкою буде точка 0. Пояснимо це на наступному прикладі.

Приклад. Розглянемо ряд

(1)

Цей ряд є сумою двох рядів

()

і

()

Кожен з двох останніх рядів є геометричною прогресією і відповідно їх суми дорівнюють та і ряд () збіжний в області , а ряд () – в крузі . Звідси маємо, що

причому ця рівність правильна в кільці (див. рис. 31). Зазначимо, що одержаний розклад не є розкладом якоїсь функції в проколеному околі точки 0.

Функція, що є сумою цього ряду є аналітичною в околі точки 0. Тому не можна стверджувати, дивлячись на ряд (1), що точка 0 є для суми цього ряду, наприклад, істотньо особливою.