§2 Степеневі ряди в комплексній області

Означення. Ряд виду , де − комплексні числа, а − фіксована комплексна точка називається степеневим рядом.

Міркуючи аналогічно як із степеневими рядами на дійсній прямій, ми переходом до ряду з модулів із застосуванням радикальної ознаки Коші одержуємо, поклавши :

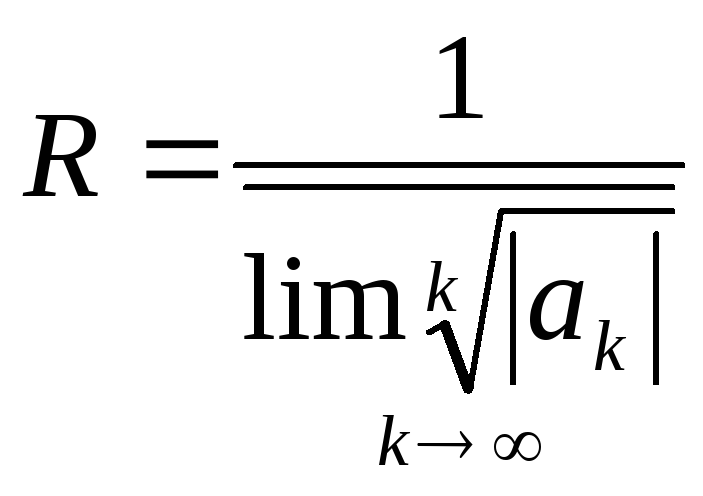1. при наш ряд буде збіжним,

2. при 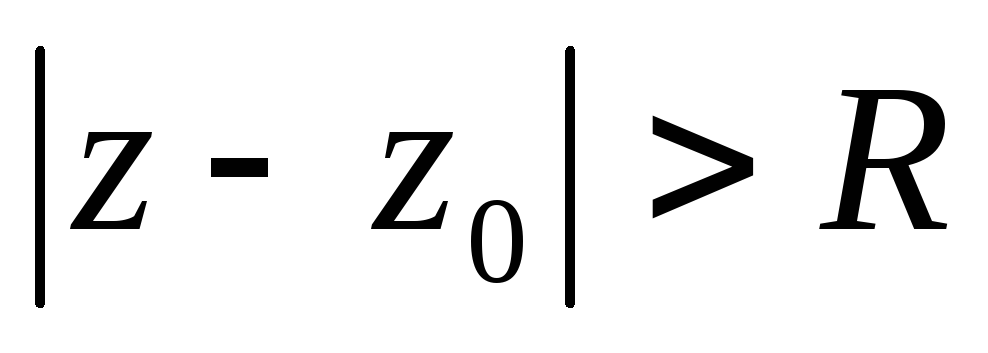− розбіжним,

3. при 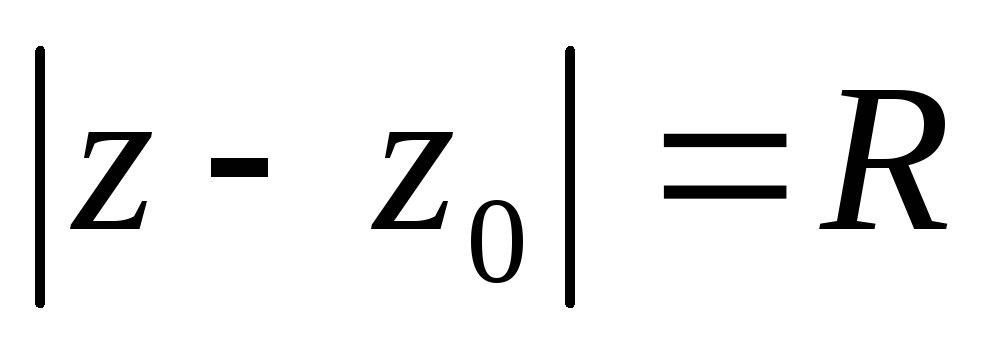− питання відкрите.

Це при умові, коли скінченне число відмінне від 0, якщо , то збіжність буде лише в точці , якщо , точок розбіжності не буде.

Ми бачимо, що з кожним степеневим рядом із скінченним і відмінним від 0 радіусом збіжності пов'язаний круг , в якому цей ряд є збіжним. Цей круг називають кругом збіжності степеневого ряду. Він може вироджуватися в точку () або у всю комплексну площину ().

Апелюючи до відповідного матеріалу з аналізу на дійсній прямій, навіть тими самими методами ми покажемо спочатку, що кожен степеневий ряд з відмінним від 0 радіусом збіжності рівномірно збіжний на довільній замкненій підмножині круга . А значить він рівномірно збіжний всередині круга збіжності. Тому звідси за теоремою Вейєрштрасса зразу маємо, що сумою цього ряду є функція аналітична в крузі . Причому має місце рівність

.

Підставивши в останню рівність , будемо мати:

.

А значить цей ряд через свою суму може бути записаний так: . Отже, ми встановили, що кожен степеневий ряд з відмінним від 0 радіусом збіжності є рядом Тейлора для своєї суми. Звідси зокрема зразу випливає наступний факт:

Якщо два степеневі ряди

, (1)

(2)

з відмінним від 0 радіусом збіжності мають одну і ту ж суму в деякому околі точки , то їх коефіцієнти рівні. А значить і суми цих рядів співпадатимуть в крузі їх збіжності.

Попередній результат стверджує, що степеневі ряди співпадають, якщо їх суми співпадають в деякому околі точки . Виявляється, що має місце сильніший результат:

Теорема 1. Якщо суми рядів (1) і (2) співпадають на множині , для якої точка є граничною, то коефіцієнти цих рядів теж співпадають і отже, суми їх співпадають в крузі збіжності цього ряду.

Доведення

З умови теореми маємо, що існує послідовність точок : . Оскільки , то матимемо, що

.

З неперервності функцій і в точці і прямуванні переходом до границі при зразу одержимо, що . Тоді в точках послідовності :

.

Звідси, міркуючи як і вище, одержимо: . Продовжуючи цей процес і т. д. ми одержимо: , . І отже, відповідні коефіцієнти рядів (1) і (2) співпадають і значить їх суми також співпадатимуть на всьому крузі збіжності цього ряду. Теорема доведена.

При введенні поняття аналітичності функції ми передбачували, що така функція може мати в області властивості, яких не мають диференційовні на дійсній прямій функції. Деякі з них ми вже розглянули і на черзі наступний важливий результат.

Теорема 2. (Коші, про розклад аналітичної в області функції в степеневий ряд)

Нехай − функція аналітична і однозначна функція в області і − довільна точка цієї області. Тоді в крузі , де − відстань від точки до межі області , дана функція розкладається в степеневий ряд

.

Зауважимо, що аналогічного результату в дійсному аналізі немає, бо там з існування похідної на якомусь інтервалі не тільки не випливає розклад по степенях , , а й навіть існування похідної, наприклад другого порядку, в точці .