§3 Інтегральна формула Коші та наслідки з неї

Теорема 1. (Інтегральна формула Коші)

Нехай аналітична в деякій області функція і проста замкнена спрямлювана крива, яка повністю належить області разом з областю, яку вона обмежує. Тоді для , що належить внутрішності кривої , справедлива рівність,

. (1)

Зауважимо, що інтеграл справа в (1) називається інтегралом Коші. Відмітною рисою такого інтеграла є:

1. він береться по замкненій кривій,

2. функція аналітична в області, яка містить цю криву разом з її внутрішністю,

3. підінтегральна функція має такий вигляд: .

Доведення

Оскільки точка належить внутрішності кривої , то існує , який повністю належить цій внутрішності разом з колом – межею цього околу. Нехай коло : . Розглянемо далі функцію в області, яка є внутрішністю кривої і зовнішністю кривої одночасно (див. рис. 26). Очевидно, що функція в цій області є аналітичною. Тоді за інтегральною теоремою Коші для системи контурів, умови якої тут повністю виконуються, будемо мати, що

.

Очевидно на тут накладається лише одна умова: щоб коло належало внутрішності кривої . А отже , остання рівність справедлива при всіх достатньо малих і значить для доведення формули (1) достатньо показати рівність,

. (2)

В зв’язку з тим, що нам треба довести (2), розглянемо величину,

. (3)

Оскільки функція є аналітичною в області, то вона неперервна в області, зокрема в нашій точці . А значить для , : : . Звідси і з (3) будемо мати для ,

.

А отже, ми одержали рівність (2), з якої і випливає формула (1). Теорема доведена.

Зауважимо, що якщо в попередній теоремі точка лежить у зовнішності кривої , то інтеграл справа як випливає з інтегральної теореми Коші буде дорівнювати 0 ( бо підінтегральна функція в області дещо ширшій, ніж внутрішність кривої , є аналітичною ).

Попрацюємо зараз з доведеною рівністю (1). В якості кривої в цій формулі ми можемо взяти коло з центром в точці і радіусом (не дуже великим). Рівнянням кола буде, . Тоді рівність (1) запишемо так,

.

Одержана рівність означає:

Значення аналітичної в області функції в точці цієї області дорівнює середньому арифметичному тих значень, які вона приймає в точках кола з центром в точці , яке повністю разом зі своєю внутрішністю належить області .

Оскільки функція є аналітичною на колі , то вона і неперервна на цьому колі і оскільки остання множина є компактом в , то функція досягає на цьому колі свого найбільшого значення. Позначимо . Тоді, якщо , то будемо мати з (1),

, .

З цієї нерівності випливає такий наслідок:

Наслідок 1. Модуль аналітичної в області функції не може досягти строгого максимуму ні в одній внутрішній точці цієї області.

Як ми говорили інтеграл справа в (1), який задовольняє відміченим вище вимогам, називається інтегралом Коші. Дещо зменшимо вимоги на такий інтеграл:

1. крива не обов’язково замкнена,

2. функцію задаватимемо тільки на і вимагатимемо її неперервності в точках цієї кривої. Звісно такий інтеграл вже не буде інтегралом Коші і рівності (1) теж не буде, але такий інтеграл ми зараз розглядатимемо і називатимемо його інтегралом типу Коші. Звісно, якщо ми для такого одержимо якусь інформацію, то вона тим більше буде вірною для інтеграла Коші.

Оскільки інтеграл визначений в кожній точці комплексної площини, за винятком точок кривої , і при кожному такому цей інтеграл дорівнює якомусь числу, то цей інтеграл задає на всій комплексній площині, за винятком кривої , деяку однозначну функцію . Покажемо, що утворена функція в кожній точці, вказаної вище, області має похідну довільного порядку, причому справедлива рівність:

, (4)

Доведемо рівність (4) методом математичної індукції. Ясно, що (4) вірна при . Припустимо, що рівність (4) справедлива при , і покажемо, що вона справедлива при . Тобто покажемо, що справедлива рівність

.

Нехай − точка, яка не належить кривій . Позначимо через − круг з центром в точці і радіусом , який з ніяких спільних точок не має, − коло цього круга, точка − довільна точка з круга , − відстань між кривими і , − круг, який містить і криву і криву ( див. рис. 27). Розглянемо різницю

Покладемо в останній рівності , , . Будемо мати,

Отже, ми одержали, що

.

Нам треба показати, що величина при прямує до числа

. (5)

Тому розглянемо різницю,

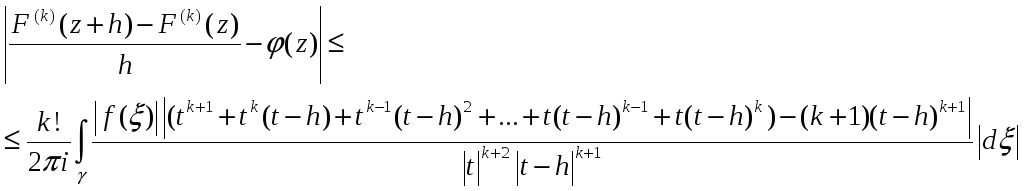(6)

Позначимо

і оцінимо .

Отже, маємо . Звідси і з (6) будемо мати

,

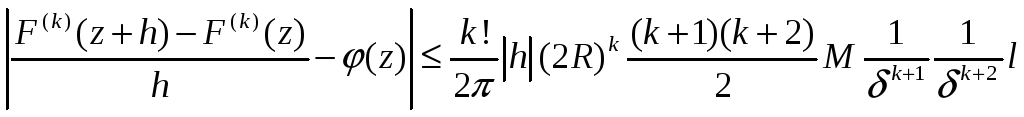де − довжина кривої . Оскільки величина − це константа, то права частина останньої нерівності при теж прямує до 0. А отже, прямує до .

З іншого боку . Таким чином маємо,

,

а значить рівність (5) і отже, формула (3) одержані.

Тут в доведенні на кривій , який існуватиме, бо − неперервна на , а − замкнена і обмежена в .

Як ми вже відмічали вище, формула аналогічна до (3) буде справедливою і для інтеграла Коші. Але з того, що для інтеграла Коші (див. (1)) , то інтегральна формула Коші і тільки що одержана формула (3) дозволяють стверджувати наступне.

Наслідок 2. Якщо функція аналітична в області , то в кожній точці цієї області вона має похідні довільного порядку і справедлива рівність

, (6)

де і − те ж що в інтегральній формулі Коші.

Наслідок 3. Похідна кожної аналітичної в області функції сама є аналітичною в цій же області функцією.

Наступне твердження, яке ми одержимо із наслідку 2, є оберненим до інтегральної теореми Коші.

Теорема (Морера)

Нехай однозначна неперервна в однозв’язній області функція. Якщо , де − довільний трикутний контур, який належить області , то − аналітична в області функція.