Доведення

Візьмемо на кривій довільну точку і сполучимо цю точку з деякою точкою на кривій неперервною кривою . На кривій візьмемо довільну точку і сполучимо її деякою кривою з деякою точкою на кривій і т. д. на кривій візьмемо точку і сполучимо її неперервною кривою з деякою точкою на кривій . Причому будемо так робити з’єднання, щоб криві повністю належали області і ніяких інших спільних точок, крім вказаних нами, з і не мали (див. рис. 24).

Утворимо далі дві області і , які обмежені частинами кривих і та кривими . Перша з областей обмежена кривими , , , , ,…, , . Друга область обмежена кривими , -, , -, ,…, - . Обидві області і повністю належать області і, на відміну від останньої, є однозв’язними. Значить інтеграли від даної нам функції по обох кривих, що обмежують ці області дорівнюють 0. Тобто

і ,

де і − криві, що обмежують області і відповідно. Тоді за адитивністю інтеграла, якщо додати останні дві рівності і врахувавши, що там будуть інтеграли по кривих і -, які в сумі дадуть 0, а також те, що наші обходи кривих і дадуть обхід кривої у від’ємному напрямку, будемо мати,

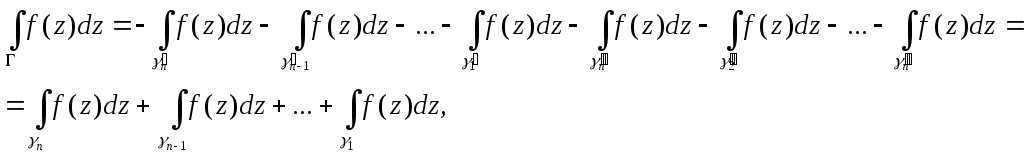
Де всі і проходяться в додатному напрямку. Теорема доведена.

Використовуючи попередній матеріал можна, подібно до того як робилося в дійсному аналізі, вийти на первісні функції, задані в комплексній області. Нехай в деякій однозв’язній області задана аналітична функція . Візьмемо в цій області довільні точки і та спробуємо з’ясувати чи залежатиме величина інтеграла від кривої , яка сполучає точки і .

З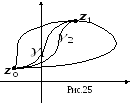’єднаємо точки і двома довільними спрямлюваними кривими і , утворимо з них замкнену криву (див. рис. 25) та застосуємо до цієї кривої і заданої функції теорему Коші. Будемо мати,

або, ,

а це означає, що величина цього інтеграла не залежить від шляху інтегрування (в області ), а залежить тільки від початкової і кінцевої точок. Це дає нам можливість, зафіксувавши точку , розглядати в цій області деяку нову функцію

.

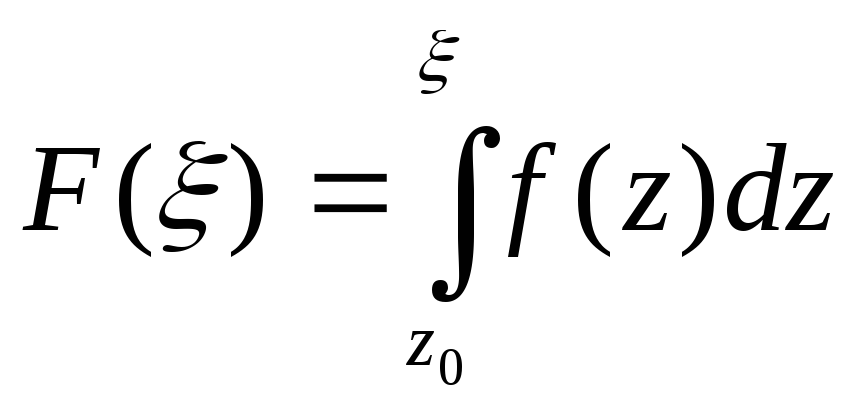Таким чином, можна висловити гіпотезу, що тут є аналогія з тим, що було в інтегралі Рімана (див. інтеграл із змінною верхньою межею). Дійсно, міркуючи так як там, легко показати, що функція буде не тільки однозначною в області , а й аналітичною в цій області і для матиме місце рівність

.

А отже, так як і там ми функцію будемо називати первісною до функції в області . І як і там одержимо аналог формули Ньютона-Лейбніца, згідно з якою будемо мати,

.

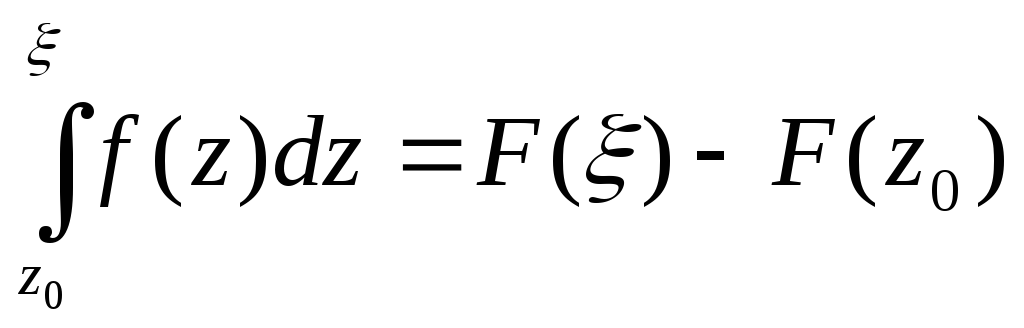Оскільки функція є аналітичною на площині, то

.

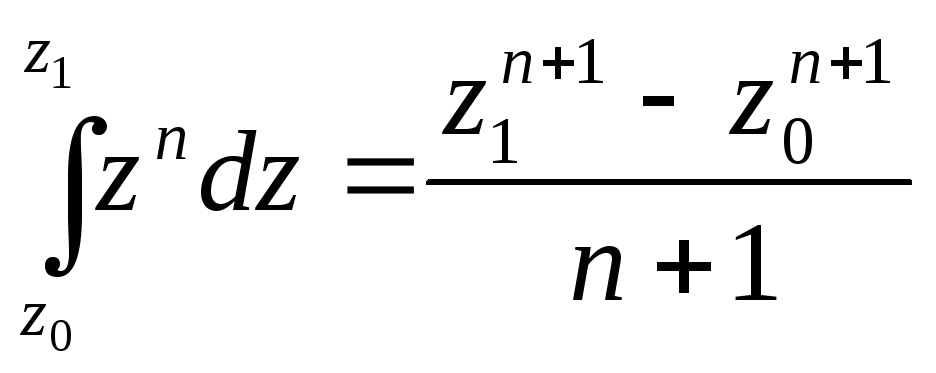Аналогічні формули будуть справедливі для і і ін.

Зауважимо, що якщо область не є однозв’язною, то все сказане вище не обов’язково буде виконуватися. І тоді введена вище функція не зобов’язана бути однозначною (її значення буде залежати від шляху інтегрування). Для так введеної многозначної функції можна спеціальним чином виділяти однозначні вітки. Використовуючи ці ідеї можна через інтеграл означити логарифмічну функцію в комплексній області. Все це можна знайти в Давидов Т.3 (ТАФ).

Використовуючи доведену вище інтегральну теорему Коші для системи контурів, можна довести основну для всієї теорії аналітичних функцій інтегральну формулу Коші.