Доведення

Припустимо, що це не так. Тобто існує точка : і для . Тоді остання нерівність буде виконуватися в якомусь околі точки , який попадає в область . Зрозуміло, що , бо в протилежному випадку ми мали б, що в околі і за тільки що доведеною теоремою єдиності ми мали б, що в області , що ми заперечуємо. Покажемо зараз, що у всіх точках околу . Припустимо, що це не так, тобто існує точка : , . Розглянемо коло з центром в точці . Оскільки є функція неперервна в області (бо функція аналітична тут), то цей модуль є неперервною функцією і на колі , а значить і в точці . Отже, ми можемо знайти на колі дугу , яка містить точку , у всіх точках якої . Оскільки ця дуга є обмеженою і замкненою множиною (тобто компактом в ), то на цій дузі існує точка, в якій функція набирає найбільшого із значень, які вона приймає в точках цієї дуги, і оскільки ця точка належить дузі кола , а у всіх точках дуги , то цей максимум на даній дузі буде якесь число , . З рівності:

. (1)

Звідси будемо мати,

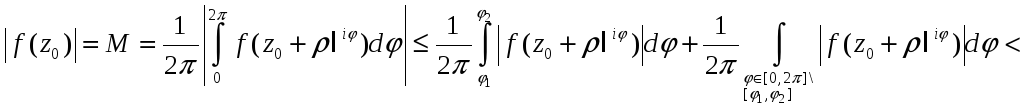
(тут при , описує дугу ).

Одержане протиріччя підтверджує, що такої точки , де б не має, зрозуміло, що і там теж не може бути. Отже, ми довели: . Присутність в останній рівності модуля ще поки що не означає, що функція . Нехай і значить для

. (2)

З аналітичності функції випливає існування всіх частинних похідних і в цьому околі. А значить рівність (2) можна диференціювати. Про диференціюємо рівність (2) по і по . Будемо мати,

, .

Об’єднаємо ці рівності в систему

.

Оскільки одержана система матиме ненульові розв’язки (бо ), то головний визначник системи дорівнює 0, тобто

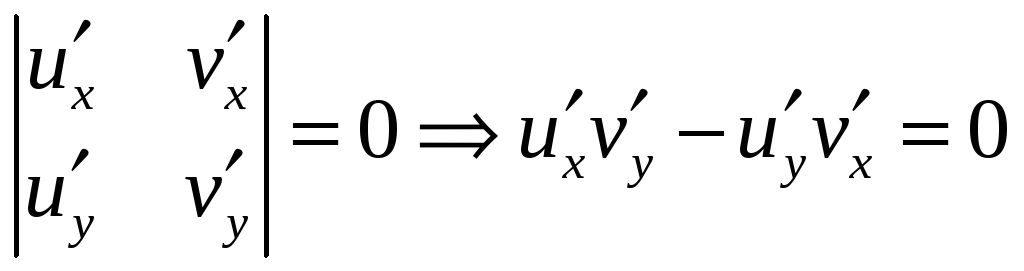
Звідси, врахувавши умови Коші-Рімана, отримуємо,

, або і аналогічно .

З останніх рівностей маємо: , , а це означає, що функція в околі , значить функція на всій області є константою, що не так. Отже, припущення про те, що є така точка , в якій модуль функції набирає найбільшого значення, невірне. А отже, вірне твердження нашої теореми. Теорема доведена.

Аналогічний результат для мінімуму модуля невірний, бо аналітична в області функція може мати нулі в цій області і звичайно в цих точках модуль її набиратиме найменшого значення (0). Якщо функція аналітична в області і не має нулів в цій області, то легко обґрунтувати, що її модуль в цій області не матиме і мінімального значення (достатньо перейти до функції і за доведеним раніше її модуль в цій області не матиме максимального значення). Таким чином, із всього сказаного вище випливає, що якщо функція неперервна в замкненій і обмеженій області і аналітична в області , то будемо мати: оскільки - компакт і функція неперервна на цьому компакті, то цей модуль досягає на свого найбільшого значення (теорема Вейєрштрасса). Оскільки з принципу максимуму модуля випливає, що ця точка, де відбувається це досягання, не може належати області , то зрозуміло, що цього максимуму модуль досягає на межі області. (Якщо до того ж в області , то цей модуль досягає і свого мінімуму на межі області ).

Використовуючи цей факт, легко одержуємо, наступний цікавий факт:

Якщо функція аналітична в області і в точках межі цієї області її модуль зберігає стале значення, то всередині цієї області існуватиме хоча б один нуль функції .

Справді, якщо припустити, що нулів нема, то і максимуму і мінімуму досягатиме на межі цієї області, а там всі значення рівні, отже, в області, а значить (див. Заключну частину доведення принципу максимуму модуля) і в області, що ми не передбачаємо.

З допомогою щойно одержаного результату доводиться наступна

Теорема. (Основна теорема алгебри)

Кожен многочлен в полі комплексних чисел має хоча б один корінь.