
- •П.1 Логарифмічна функція і її властивості ………………………………… 48
- •Розділ 1. Вступні зауваження і факти
- •§1. Комплексні числа. Операції над комплексними числами
- •§2. Збіжність послідовностей комплексних чисел
- •§3 Нескінченно віддалена точка. Розширена комплексна площина. Стереографічна проекція
- •§4 Ряди комплексних чисел
- •§5 Комплекснозначні функції комплексного аргументу та деякі їх властивості
- •Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції
- •§1 Похідна функції комплексної змінної. Критерій її існування
- •Доведення
- •§2 Геометричний зміст аргументу і модуля похідної
- •§3 Дробово-лінійна функція. Властивості і відображення здійснювані нею
- •§4 Експоненціальна і тригонометрична функції в комплексній області
- •П.1 Логарифмічна функція і її властивості
- •§5 Виділення однозначних віток многозначної функції
- •§6 Показникова та степенева функції в комплексній області
- •Розділ 3. Інтеграл в комплексній області
- •§1 Означення інтеграла від функції комплексної змінної та його властивості
- •§2 Інтегральна теорема Коші
- •Доведення
- •Доведення
- •§3 Інтегральна формула Коші та наслідки з неї
- •Доведення
- •Доведення
- •Розділ 4. Функціональні ряди в комплексній області
- •§1 Збіжність та рівномірна збіжність функціональних рядів в комплексній області. Теорема Вейєрштрасса про рівномірно збіжні ряди аналітичних функцій
- •Доведення
- •§2 Степеневі ряди в комплексній області
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§3 Ряди Лорана
- •Доведення
- •Розділ 5. Лишки та їх застосування
- •§1 Особливі точки аналітичної функції та їх класифікація
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§2. Теорема про лишки та її застосування. Обчислення лишків
- •§3 Принцип аргументу
- •Доведення
- •§4 Поняття про цілу функцію та лишки відносно нескінченно віддаленої точки
- •Висновок
- •Список використаної літератури:
Розділ 3. Інтеграл в комплексній області
§1 Означення інтеграла від функції комплексної змінної та його властивості
Нехай
![]() − деяка спрямлювана крива в
− деяка спрямлювана крива в
![]() -
площині і
-
площині і
![]() − деяка комплексно-значна функція
комплексного аргументу. Крім цього
нехай дана функція визначена на кривій
− деяка комплексно-значна функція
комплексного аргументу. Крім цього
нехай дана функція визначена на кривій
![]() .
Спробуємо перенести на ці два об’єкти
конструкцію, яка привела нас до
криволінійного інтеграла 2-го роду. З
цією метою візьмемо
.
Спробуємо перенести на ці два об’єкти
конструкцію, яка привела нас до
криволінійного інтеграла 2-го роду. З
цією метою візьмемо
![]() -
розбиття кривої
-
розбиття кривої
![]() точками
точками
![]() ,
,
![]() ,
,
![]() ,...,
,...,![]() .
На кожній з елементарних дуг
.
На кожній з елементарних дуг
![]() візьмемо по точці
візьмемо по точці
![]() і утворимо суму
і утворимо суму
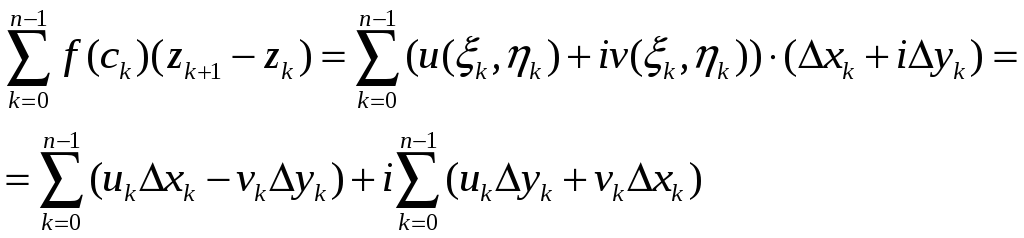 ,
,
яка
називається інтегральною
сумою для
функції
![]() для кривої
для кривої
![]() .
.
Означення.
Якщо при прямуванні до 0 кроку розбиття
кривої
![]() існуватиме границя цієї суми, яка не
залежатиме ні від способу розбиття цієї
кривої , ні від способу вибору точок на
елементарних дугах, то її ми називатимемо
інтегралом
від функції комплексної змінної по
кривій
існуватиме границя цієї суми, яка не
залежатиме ні від способу розбиття цієї
кривої , ні від способу вибору точок на
елементарних дугах, то її ми називатимемо
інтегралом
від функції комплексної змінної по
кривій
![]() і
позначатимемо
і
позначатимемо
![]() .
.
Наявність вище одержаної рівності дозволяє нам стверджувати, що існування такого інтеграла зв’язане з існуванням 2-х наступних криволінійних інтегралів
![]() і
і
![]() .
.
Як ми
знаємо з теорії криволінійних інтегралів,
останні два існують, якщо крива
![]() кусково-гладка, а функції
кусково-гладка, а функції
![]() і
і
![]() є неперервними на цій кривій. Оскільки
неперервність функцій
є неперервними на цій кривій. Оскільки
неперервність функцій
![]() і
і
![]() рівносильна неперервності функції
рівносильна неперервності функції
![]() ,
то можна стверджувати:
,
то можна стверджувати:
Якщо
функція
![]() неперервна на гладкій кривій
неперервна на гладкій кривій
![]() (
(
![]() ,
,
![]() і
і
![]() −
неперервні разом із своїми похідними
на
−
неперервні разом із своїми похідними
на
![]() ),
то існуватиме
),
то існуватиме

Остання формула вирішує в багатьох випадках проблему обчислення інтеграла від функції комплексної змінної.
Розглянемо деякі властивості введеного вище інтеграла.
-
З’ясуємо чи тут має значення напрям проходження кривої
 .
Простий аналіз означення інтеграла
показує, що
.
Простий аналіз означення інтеграла
показує, що
![]() .
.
Тобто при зміні напрямку інтегрування по кривій знак інтеграла змінюється на протилежний.
-
Якщо криву
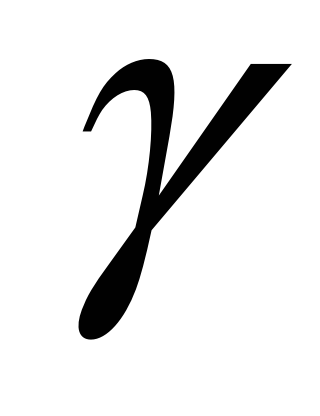 точками розбити на скінченну кількість
кривих
точками розбити на скінченну кількість
кривих
 -х
без внутрішніх спільних точок, то
-х
без внутрішніх спільних точок, то
![]() .
.
3)
![]() .
.
4) Ця властивість дає можливість робити оцінки інтеграла від функції комплексної змінної:
 ,
де
,
де
![]() −
диференціал дуги.
−
диференціал дуги.
Зауважимо, що справа стоїть криволінійний інтеграл 1-го роду. Доведення цієї нерівності одержується з самого означення інтеграла в комплексній області.
Часто ми будемо користуватися наслідком цієї нерівності:
![]() )
Якщо функція
)
Якщо функція
![]() є обмеженою на кривій
є обмеженою на кривій
![]() ,
тобто
,
тобто
![]() :
:
![]()
![]()
![]() ,
то
,
то
 ,
де
,
де
![]() − довжина кривої
− довжина кривої
![]() .
.
Що стосується відомої із дійсного аналізу теореми про середнє, то відповідь на те чи буде вона мати місце, буде дана дещо пізніше.
Зауважимо, що ми тут часто матимемо справу з інтегралом по замкненій кривій. Домовимося, що якщо не сказано в якому напрямку проходиться ця крива, то будемо брати той напрям, щоб область, яка обмежена цією кривою, залишалася зліва від спостерігача, що проходить криву.
Обчислимо декілька інтегралів від функції комплексної змінної:
1)
![]() .
.
Зауважимо,
що величина цього інтеграла зовсім не
залежить від кривої
![]() ,
а залежить від точок
,
а залежить від точок
![]() і
і
![]() ,
зокрема, якщо крива замкнена, то цей
інтеграл дорівнює 0.
,
зокрема, якщо крива замкнена, то цей
інтеграл дорівнює 0.
2)
![]()
![]() .
.
Останню
рівність одержимо, взявши
![]() -
розбиття і в якості точок
-
розбиття і в якості точок
![]() візьмемо праві (ліві) кінці дуг розбиття.
З останньої рівності видно, що величина
інтеграла не залежить від форми кривої,
а залежить від початкової і кінцевої
її точок. Якщо крива замкнена, то цей
інтеграл теж рівний 0.
візьмемо праві (ліві) кінці дуг розбиття.
З останньої рівності видно, що величина
інтеграла не залежить від форми кривої,
а залежить від початкової і кінцевої
її точок. Якщо крива замкнена, то цей
інтеграл теж рівний 0.
3)
![]()
 ,
,
нехай
![]() −
коло
з центром в точці
−
коло
з центром в точці
![]() і
радіусом
і
радіусом
![]() ,
тоді
,
тоді
![]() .
.
