
- •П.1 Логарифмічна функція і її властивості ………………………………… 48
- •Розділ 1. Вступні зауваження і факти
- •§1. Комплексні числа. Операції над комплексними числами
- •§2. Збіжність послідовностей комплексних чисел
- •§3 Нескінченно віддалена точка. Розширена комплексна площина. Стереографічна проекція
- •§4 Ряди комплексних чисел
- •§5 Комплекснозначні функції комплексного аргументу та деякі їх властивості
- •Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції
- •§1 Похідна функції комплексної змінної. Критерій її існування
- •Доведення
- •§2 Геометричний зміст аргументу і модуля похідної
- •§3 Дробово-лінійна функція. Властивості і відображення здійснювані нею
- •§4 Експоненціальна і тригонометрична функції в комплексній області
- •П.1 Логарифмічна функція і її властивості
- •§5 Виділення однозначних віток многозначної функції
- •§6 Показникова та степенева функції в комплексній області
- •Розділ 3. Інтеграл в комплексній області
- •§1 Означення інтеграла від функції комплексної змінної та його властивості
- •§2 Інтегральна теорема Коші
- •Доведення
- •Доведення
- •§3 Інтегральна формула Коші та наслідки з неї
- •Доведення
- •Доведення
- •Розділ 4. Функціональні ряди в комплексній області
- •§1 Збіжність та рівномірна збіжність функціональних рядів в комплексній області. Теорема Вейєрштрасса про рівномірно збіжні ряди аналітичних функцій
- •Доведення
- •§2 Степеневі ряди в комплексній області
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§3 Ряди Лорана
- •Доведення
- •Розділ 5. Лишки та їх застосування
- •§1 Особливі точки аналітичної функції та їх класифікація
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§2. Теорема про лишки та її застосування. Обчислення лишків
- •§3 Принцип аргументу
- •Доведення
- •§4 Поняття про цілу функцію та лишки відносно нескінченно віддаленої точки
- •Висновок
- •Список використаної літератури:
Доведення
Візьмемо
![]() .
Очевидно, що існує коло
.
Очевидно, що існує коло
![]() таке,
що точка
таке,
що точка
![]() лежить в середині цього кола (не на
колі). З того, що функція
лежить в середині цього кола (не на
колі). З того, що функція
![]() аналітична в області
аналітична в області
![]() і з того як розміщується точка
і з того як розміщується точка
![]() відносно кола
відносно кола
![]() (і де лежить
(і де лежить
![]() )за
інтегральною формулою Коші будемо мати,
)за
інтегральною формулою Коші будемо мати,
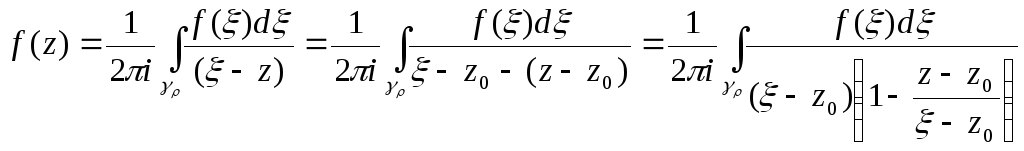 (1)
(1)
Розглянемо
функцію
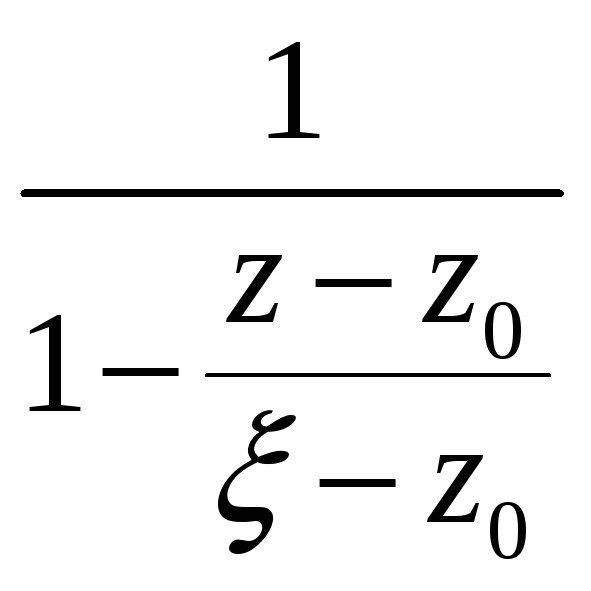 .
Для неї
.
Для неї
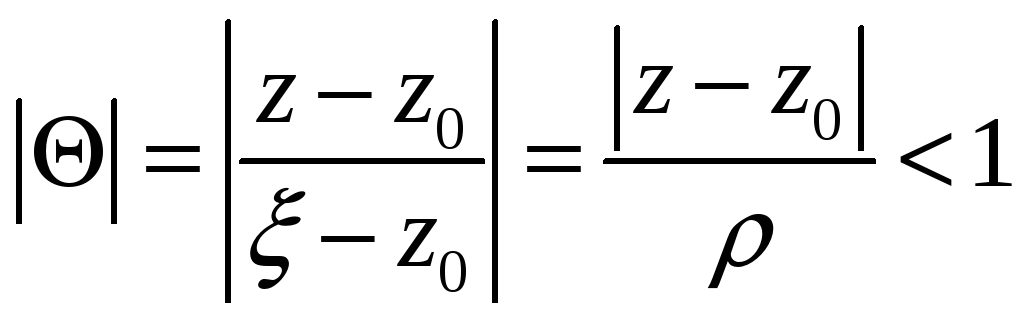 ,
,
![]() ,
а раз так, то остання функція є сумою
геометричної прогресії із знаменником
,
а раз так, то остання функція є сумою
геометричної прогресії із знаменником
![]() і тому будемо мати,
і тому будемо мати,
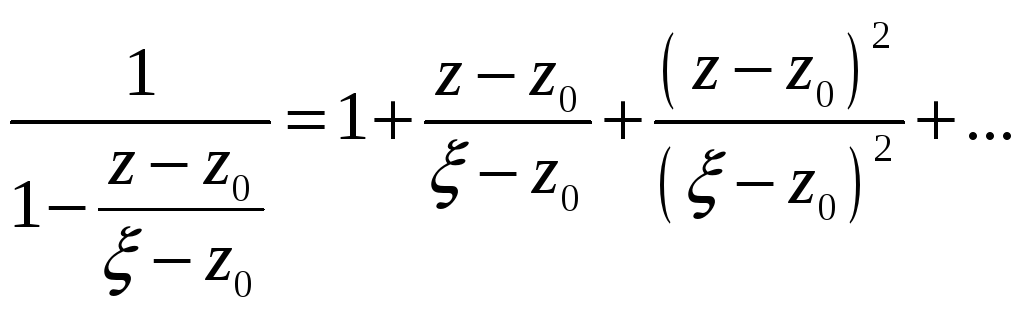 ,
(2)
,
(2)
причому
цей ряд на колі
![]() є рівномірно збіжний. Розглянемо функцію
є рівномірно збіжний. Розглянемо функцію
![]() на колі
на колі
![]() .
Для неї справедлива нерівність,
.
Для неї справедлива нерівність,
![]() ,
,
де
![]() ,
,
![]() ,
а отже, ця функція є обмеженою на колі
,
а отже, ця функція є обмеженою на колі
![]() .
Значить ряд (2) можна на неї домножити і
він залишиться на
.
Значить ряд (2) можна на неї домножити і
він залишиться на
![]() рівномірно
збіжним. Звідси і з рівності (1), підставивши
в інтеграл (1) замість підінтегральної
функції ряд, який одержується з (2)
домноженням на
рівномірно
збіжним. Звідси і з рівності (1), підставивши
в інтеграл (1) замість підінтегральної
функції ряд, який одержується з (2)
домноженням на
![]() і можливістю почленного інтегрування
ряду будемо мати,
і можливістю почленного інтегрування
ряду будемо мати,
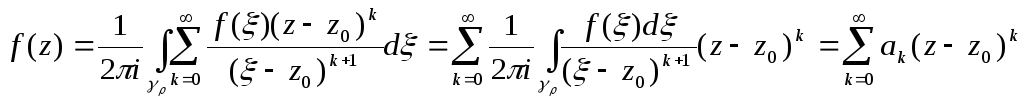 ,
,
де
![]() (3)
(3)
і
отже, потрібний нам розклад в крузі
![]() одержаний. Формула (3) дає можливість
обчислювати коефіцієнти цього степеневого
ряду. Теорема
доведена.
одержаний. Формула (3) дає можливість
обчислювати коефіцієнти цього степеневого
ряду. Теорема
доведена.
Таким
чином теорема 2, взагалі кажучи, не тільки
стверджує можливість розкладу в
степеневий ряд у відповідному крузі,
але й формулою (3) дає можливість знаходити
коефіцієнти розкладу. (Тут коло
![]() −
довільне коло з центром в точці
−
довільне коло з центром в точці
![]() ,
яке лежить в крузі
,
яке лежить в крузі
![]() ). Помноживши обидві частини формули
(3) на
). Помноживши обидві частини формули
(3) на
![]() ми, скориставшись інтегральною формулою
Коші отримаємо:
ми, скориставшись інтегральною формулою
Коші отримаємо:
![]()
![]() .
(4)
.
(4)
Це ще одна формула для обчислення коефіцієнтів розкладу. Але на практиці легко користуватися формулами (3), коли похідна довільного порядку легко шукається.
Розклади
синуса, косинуса і експоненти ми мали
з самого означення. Використовуючи
формулу (4), можна одержати розклади
довільної вітки
![]() по степенях
по степенях
![]() ,
а звідси розклад якої-небудь вітки
,
а звідси розклад якої-небудь вітки
![]() по степенях
по степенях
![]() .
Аналогічно можна зробити і з функцією
.
Аналогічно можна зробити і з функцією
![]() (з якою-небудь її віткою) по степенях
(з якою-небудь її віткою) по степенях
![]() ,
а звідси одержимо розклад по степенях
,
а звідси одержимо розклад по степенях
![]() і
звідси одержимо також біноміальний
ряд.
і
звідси одержимо також біноміальний
ряд.
Зауважимо, що і в комплексному аналізі при розкладі функції в степеневий ряд теж переважно користуються не формулами (3) і (4), а відомими класичними розкладами і якимось штучними прийомами.
Повернемося
знову до доведеної вище теореми. По-перше,
якщо областю аналітичності є вся
комплексна площина, то
![]() .
На практиці, якщо область аналітичності
не вся комплексна площина, то
.
На практиці, якщо область аналітичності
не вся комплексна площина, то
![]() практично означає відстань від точки
практично означає відстань від точки
![]() до найближчої особливої точки цієї
функції. По-друге зауважимо, що одержані
результати дозволяють прояснити
ситуацію, чому деякі функції на дійсній
прямій розкладаються в ряд на якомусь
інтервалі скінченої довжини, хоча вони
на всій прямій мають гарні властивості.
Так, наприклад, функція
до найближчої особливої точки цієї
функції. По-друге зауважимо, що одержані
результати дозволяють прояснити
ситуацію, чому деякі функції на дійсній
прямій розкладаються в ряд на якомусь
інтервалі скінченої довжини, хоча вони
на всій прямій мають гарні властивості.
Так, наприклад, функція
![]() і цей розклад має місце тільки на
інтервалі
і цей розклад має місце тільки на
інтервалі
![]() ,
хоча сама функція є «гарною» на всій
числовій прямій. Пояснює це явище вихід
в комплексну область, на якій функція
,
хоча сама функція є «гарною» на всій
числовій прямій. Пояснює це явище вихід
в комплексну область, на якій функція
![]() має на колі
має на колі
![]() дві особливі точки
дві особливі точки
![]() та
та
![]() .
Повернемося тепер до формули (3). Будемо
мати,
.
Повернемося тепер до формули (3). Будемо
мати,
![]() .
.
Ми
отримали, що для
![]()
![]() .
(5)
.
(5)
Нерівності (5) називають нерівностями Коші для коефіцієнтів степеневого ряду. З цих нерівностей в якості наслідку випливає
Теорема 3. (Ліувіль)
Кожна аналітична і обмежена на всій комплексній площині функція є константою.
