§2 Інтегральна теорема Коші

Аналізуючи приклади інтегралів, обчислених в попередньому параграфі, можна зробити висновок, що інтеграли по замкненому контуру від деяких функцій дорівнюють 0. Наступна теорема, яка є однією з основних в теорії аналітичних функцій, дає достатні умови рівності 0 інтегралів від деяких функцій по деяких кривих.

Теорема (Інтегральна теорема Коші)

Якщо функція аналітична в однозв’язній області і − довільна замкнена спрямлювана крива в цій області, то

.

Доведення

Нехай спочатку є трикутний контур, який лежить в області , тобто − це трикутник (див рис. 20 ). Покажемо, що . Позначимо . Ясно, що . Нам треба довести, що . Проведемо в цьому трикутнику всі 3 середні лінії. Ці середні лінії розіб’ють трикутник на 4 трикутники: , , , . Тоді . З останньої рівності будемо мати:

. А якщо так, то обов’язково знайдеться принаймні один з 4-х трикутників, позначимо його через , такий, що . Зробивши з трикутником те саме, що ми зробили з трикутником , ми знайдемо трикутник , такий, що 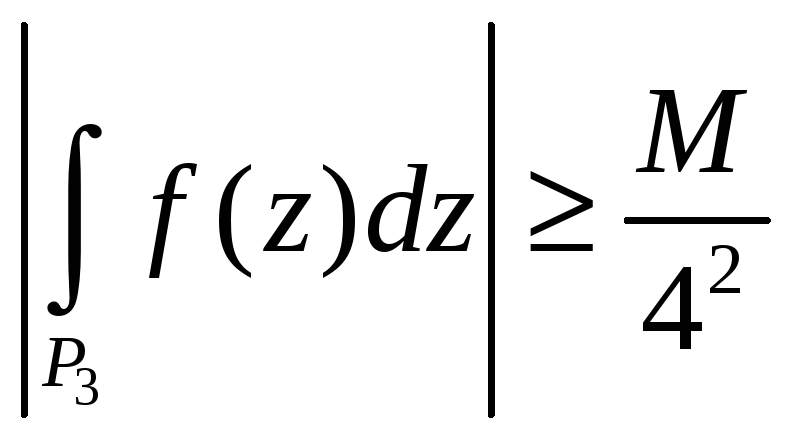. Продовжуючи цей процес і так далі ми утворимо послідовність трикутних контурів , , ,... , про які можна сказати таке:

1) ;

2) Периметр трикутника , де − периметр трикутника ;

3) .

Оскільки трикутники утворюють послідовність вкладених ком пактів, діаметр яких прямує до 0, то за відомою з функціонального аналізу теоремою будемо мати, що , яка належить всім трикутникам . Оскільки всі трикутники належать області і − однозв’язна, то точка , а значить функція диференційовна в цій точці (бо - аналітична в області ). Тоді

.

А це означає, що

, : і

або

. (1)

Оскільки точка − це єдина спільна точка для всіх наших трикутників і всі вони стягуються в цю точку, то очевидно, починаючи з деякого номера , всі трикутники належатимуть . А якщо так, то для матимемо, що . Таким чином, для таких матимемо на основі співвідношення (1), що для справедлива нерівність,

. (2)

Обчислимо, врахувавши перші два інтеграли кінця попереднього параграфа,

.

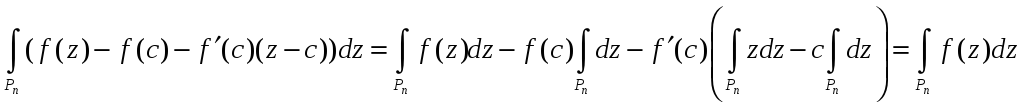Звідси і з (2) будемо мати,

.

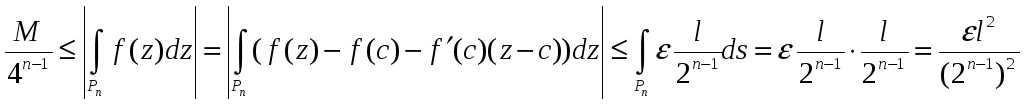З останньої рівності будемо мати, , а оскільки довільне, то зразу одержуємо, що , а значить і теорема Коші для випадку трикутного контуру доведена.

Очевидно, використовуючи вище доведене, легко показати, що теорема буде вірна і для довільного опуклого многокутника (бо його можна розбити діагоналями, що виходять з однієї вершини на скінченну кількість трикутників). Див. рис. 21.

Якщо ми матимемо замкнену ламану , яка утворюватиме не опуклий многокутник, то очевидно цей многокутник можна буде розбити на скінченну кількість опуклих многокутників і справа зведеться до попереднього випадку.

Якщо ми маємо замкнену ламану, яка має точки само перетину, налягання одних ланок на інші, то використовуючи геометричні ідеї, легко показати, що справа зведеться до попереднього. А значить ми показали, що яку б замкнену ламану, яка лежить в області , ми не взяли, завжди інтеграл від нашої функції по цій ламаній буде дорівнювати 0.

Перехід від ламаної до довільної спрямлюваної кривої можна здійснити з допомогою леми, яку ми вивчали в криволінійних інтегралах і для функції комплексної змінної її можна сформулювати так:

Лема. Нехай неперервна в області функція і − довільна спрямлювана крива, що належить . Тоді , , існує ламана , вписана в криву , така що,

1. всі ланки ламаної належать ;

2. .

Тепер можна закінчувати доведення інтегральної теореми Коші. Нехай − довільна замкнена спрямлювана крива в цій області . Візьмемо , тоді за лемою існує ламана , вписана в цю криву і

.

Але за доведеним . Звідси маємо, що

.

Оскільки довільне і ліва частина останньої нерівності від не залежить, то одержимо, що

.

Теорема доведена.

Зауважимо що ця теорема залишається вірною і при дещо менш жорстких умовах, накладених на функцію. Нехай − замкнена спрямлювана крива, яка обмежує область . Якщо неперервна в (замикання області ) і аналітична в , то як і раніше .

Що стосується доведення цієї теореми, то воно порівняно просте для випадку зіркової області, тобто області, яка обмежена кривою, яку будь-який промінь, який виходить з внутрішності цієї кривої, перетинає її лише в одній точці. Що стосується загального випадку кривої , то доведення цієї теореми виходить за рамки нашого курсу.

Зауважимо, що інтегральну теорему Коші одержав, обчислюючи так звані інтеграли Френеля

і .

Покажемо як з допомогою теореми Коші обчислюються останні інтеграли.

Для обчислення цих інтегралів розглянемо функцію . Ця функція аналітична на . Взявши контур (див. рис.22) одержимо за інтегральною теоремою Коші . З адитивності інтеграла будемо мати

Зробимо деякі позначення.

,

.

Оцінимо , , .

, а оскільки останній інтеграл є інтегралом Пуассона, який ми в свій час вже обчислювали (), то

. (1)

Оцінимо . Оскільки , то матимемо,

. (2)

Оскільки при (див. рис. 23) і , то . Звідси і з (2) одержимо:

,

а тому, , коли .Звідси і з (1) будемо мати,

.

З останньої рівності будемо мати, що обидва інтеграли і збіжні до числа . Отже, .

Є ще декілька таких невласних інтегралів, які обчислюються так само як і інтеграли Френеля.

Інтегральна теорема Коші приводилася для функції аналітичної в однозв’язній області. Звісно вона не переноситься (ми розглядали приклад) в такому ж виді на неоднозв’язні області. Проте як наслідок з доведеної вище теореми можна одержати так звану теорему Коші для системи контурів.

Теорема (Коші, для системи контурів)

Нехай в деякій області визначена аналітична функція , і в цій області задана систем замкнутих спрямлюваних жорданових кривих , , ,…, така, що,

1) , ,…, лежать в області, яка обмежується кривою ,

2) для криві лежать у зовнішності кривої , .

3) Многозв’язна область , обмежена кривими , , ,…, (вона одержується, якщо із внутрішності кривої вилучити області обмежені кривими , ), належить області .

Тоді , причому напрям обходу всіх кривих в цій рівності додатній.