Доведення

Дивлячись на доведення інтегральної теореми Коші робимо висновок, що такий інтеграл дорівнює 0 по довільному спрямлюваному контуру, який належить області . Тоді звідси матимемо, що буде однозначною в області функцією, причому із неперервності функції випливає диференційованість функції і рівність . Значить аналітична в цій області (бо вона тут диференційовна), тому за наслідком 3 її похідна, яка дорівнює , теж аналітична в цій області. Теорема доведена.

Нехай знову − функція аналітична в деякій області . Тоді при вказаних в інтегральній теоремі Коші, умовах на , матиме місце формула (6). Будемо вважати, що − це коло . Як і раніше . Тоді з (6) матимемо,

.

Нерівності () називають нерівностями Коші. З останньої нерівності матимемо:

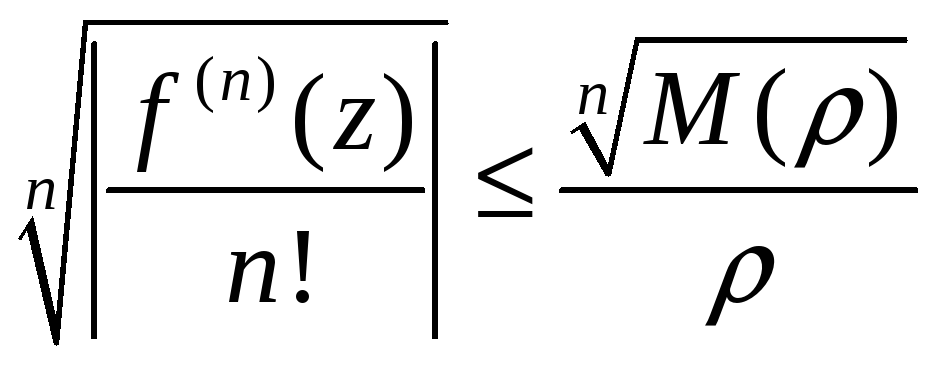(7)

Позначимо через − відстань від точки до межі області аналітичності. Тоді зрозуміло, що в попередніх викладках довільне але менше за . Візьмемо таке і зафіксуємо його. Тоді величина теж буде фіксованою і при . Звідси і нерівності (7) будемо мати,

.

Оскільки, остання нерівність правильна для , то з неї отримаємо,

.

Ми отримали співвідношення між величиною цієї верхньої границі і відстанню від точки до межі області аналітичності функції . Зокрема ця верхня границя не може бути великою, якщо відстань теж є великою і, якщо функція є аналітичною на всій площині, то і значить розглядувана верхня границя дорівнює 0. Відмітимо до слова, що функції аналітичні на всій комплексній площині називаються цілими.

Розділ 4. Функціональні ряди в комплексній області

§1 Збіжність та рівномірна збіжність функціональних рядів в комплексній області. Теорема Вейєрштрасса про рівномірно збіжні ряди аналітичних функцій

Означення 1. Ряд, членами якого є функції комплексного аргументу називається комплексно значним рядом

(1)

Означення 2. Множина , в кожній точці якої ряд (1) збіжний, називається областю збіжності цього ряду. Зрозуміло, що сумою ряду (1) буде деяка функція , яка задана в області . Очевидно те, що функція є сумою ряду (1) на мові можна записати так:

,

де .

Аналогічно, як і в дійсному аналізі, якщо в, написаному вище, означенні збіжності залежатиме тільки від і не залежатиме від , то такий ряд будемо називати рівномірно збіжним до функції .

Означення 3. Ряд (1) називається рівномірно збіжним до суми на множині , якщо

.

Зрозуміло, що із рівномірної збіжності випливає його звичайна чи поточкова збіжність, але не навпаки. Як і в дійсному аналізі можна довести, що ряд збіжний до функції в крузі , але він тут нерівномірно збіжний.

Як і в дійсному аналізі рівномірно збіжні ряди мають властивості, яких не мають поточково збіжні ряди. Зокрема

Теорема. Якщо члени ряду (1) є неперервними на деякій множині функції і цей ряд збіжний на множині рівномірно до деякої функції , то функція буде неперервною.

Теорема. Нехай члени ряду (1) є функції інтегровані на деякій спрямлюваній кривій і ряд (1) рівномірно збіжний на цій кривій до деякої функції . Тоді справедлива рівність

.

Зауважимо, що інколи корисною для теоретичних досліджень є

Теорема. (Критерій Коші рівномірної збіжності функціонального ряду)

Для того, щоб ряд (1) був рівномірно збіжний на деякій множині необхідно і достатньо щоб

.

Тут також має місце відома з дійсного аналізу ознака Вейєрштрасса рівномірної збіжності ряду, в якій для збіжності ряду підшуковується мажорантний збіжний числовий знакододатний ряд на множині .

Як виявляється в теорії аналітичних функцій суттєву роль відіграє ще й так зване поняття рівномірної збіжності всередині області .

Означення. Ряд (1) називається рівномірно збіжним всередині області , якщо він рівномірно збіжний на будь-якій замкненій і обмеженій підмножині множини .

Очевидно, що із рівномірної збіжності в області тривіально випливає рівномірна збіжність всередині області, але не навпаки. В цьому нас переконує геометрична прогресія, яка, як легко показати, рівномірно збіжна всередині одиничного круга, але не є рівномірно збіжною на всьому (відкритому) одиничному крузі.

Наступне твердження дає необхідні і достатні умови рівномірної збіжності ряду всередині деякої області.

Теорема. (Критерій рівномірної збіжності ряду всередині області)

Для того, щоб ряд (1) був рівномірно збіжний всередині області необхідно і достатньо, щоб для існував окіл, в якому цей ряд рівномірно збіжний.

(Необхідність очевидна. Достатність доводиться методом від супротивного.)

Наступна теорема є в якійсь мірі перенесенням на комплексну площину відомої з дійсного аналізу тереми про почленне диференціювання функціонального ряду.

Теорема Вейєрштрасса. (про рівномірно збіжні ряди аналітичних функцій)

Нехай ряд

(2)

аналітичних в області функцій рівномірно збіжний всередині цієї області. Тоді сума цього ряду є функцією аналітичною в цій області і ряд (2) можна почленно диференціювати в області довільну кількість разів, тобто справедлива рівність

, (3)