Доведення

Нехай маємо многочлен . Якщо , то все ясно ( − корінь многочлена). Припустимо, що . Розглянемо в - площині множину. Очевидно, що множина не порожня (бо точка 0 належить цій множині). Звісно, що множина обмежена і відкрита. Справді, із неперервності функції випливає, що якщо значення цієї функції в якійсь точці менше за якесь число, то у всіх точках достатньо близьких до точки її значення теж буде менше за це число. Отже, кожна точка , яка попадає в множину «увійде» в неї разом з деяким своїм околом і отже, точка - внутрішня точка і - відкрита множина.

Неважко показати, що в кожній межовій точці множини буде виконуватися рівність . Припустимо, що це не так. Тобто нехай в якійсь точці межі множини виконується нерівність . Тоді існує цілий окіл цієї точки , в кожній точці якого буде виконуватися остання нерівність, а отже, цілий окіл цієї точки належить до множини , а це неможливо для межової точки. Якщо припустити, що , то знайдеться цілий окіл точки , жодна точка якого не належатиме до множини . Отже, − не порожня, обмежена, відкрита множина, на межі якої функція є сталою. А це на основі попереднього і означає, що в цій множині є хоча б одна така точка, в якій . Теорема доведена.

§3 Ряди Лорана

Безпосереднім узагальненням степеневих рядів є ряди по від’ємних степенях . Розглянемо такий ряд

(1)

Заміна зводить цей ряд до степеневого ряду

(2)

Знайдемо радіус збіжності цього ряду: . Тоді,

1. якщо , то ряд (2) збіжний в точці ;

2. якщо , то ряд (2) збіжний на всій комплексній площині;

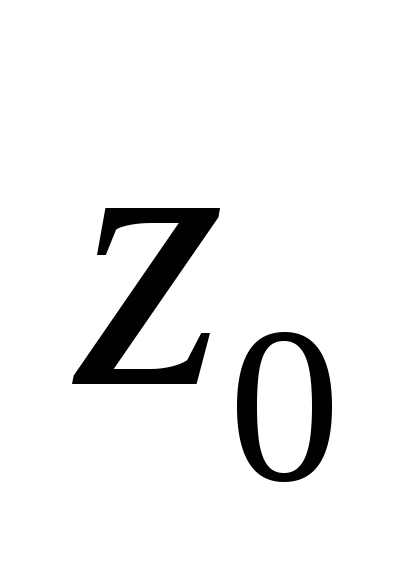3. якщо , то ряд збіжний в крузі і розбіжний на (при − невідомо).

Повертаючись до ряду (1) і звертаючи увагу на заміну, будемо мати, що

1. при ряд (1) збіжний лише в нескінченно віддаленій точці;

2. при ряд (1) збіжний на всій комплексній площині, крім точки ;

3. при 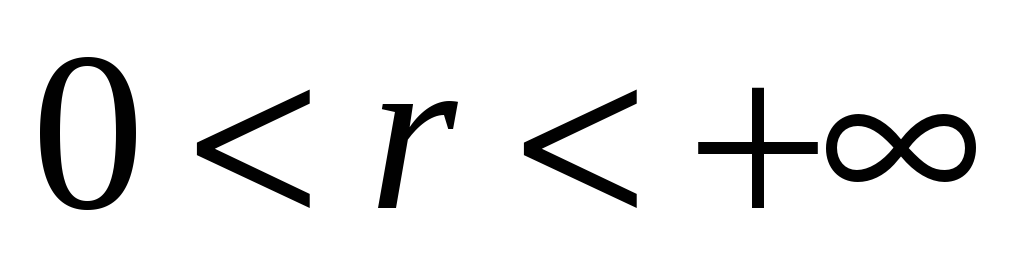ряд (1) збіжний в області і розбіжний в крузі 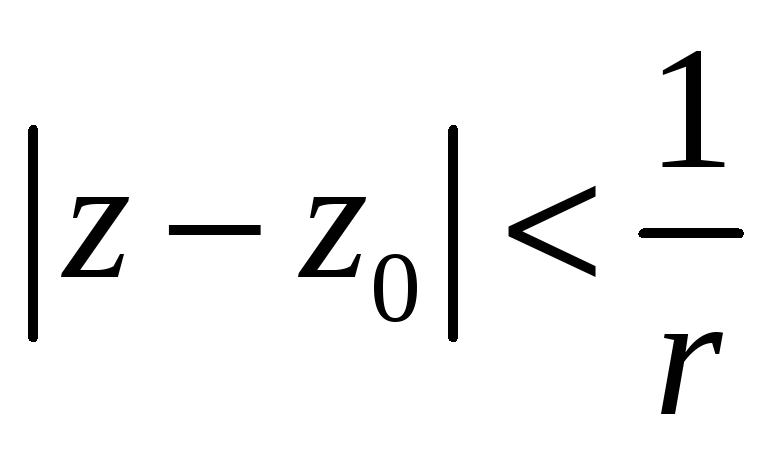. З того, що сума ряду (2) є функцією аналітичною в крузі випливає, що сума ряду (1) теж є функція аналітична в області (при ). Цей результат можна одержати і з дещо інших міркувань, а саме: у вказаній вище області члени ряду (1) є аналітичними в області функціями і якщо ми візьмемо довільну замкнену область, яка належить області 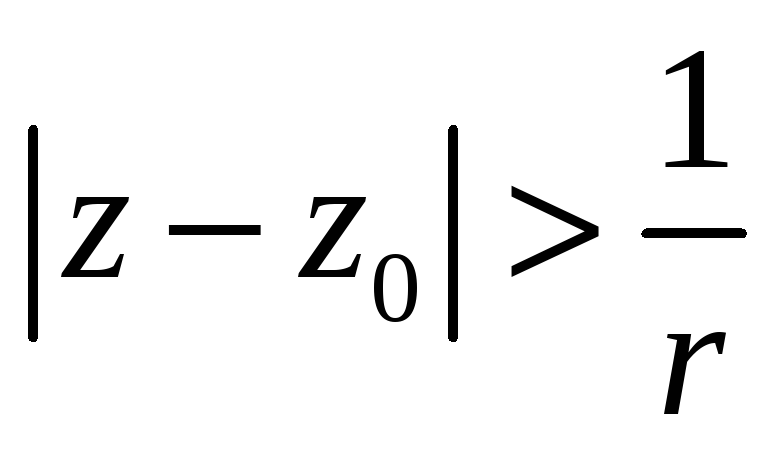, то відображення переведе її в якусь замкнену область круга , а на цій замкненій області степеневий ряд (2) збіжний рівномірно і значить на вихідній замкненій області, що належить області , ряд (1) теж збіжний рівномірно. Отже, виходить, що ряд (1) збіжний всередині області 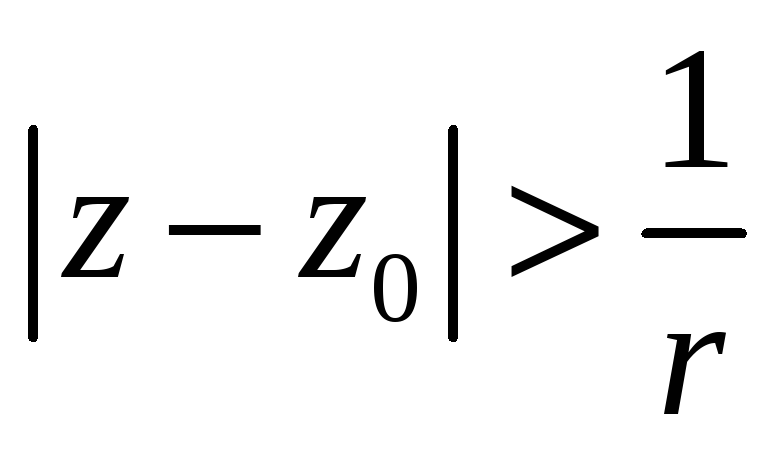. Тоді за теоремою Вейєрштрасса сума цього ряду є функція аналітична в цій області. Якщо ми маємо функцію , яка є сумою ряду (1) в області , то логічно вважати її аналітичною в нескінченно віддаленій точці і 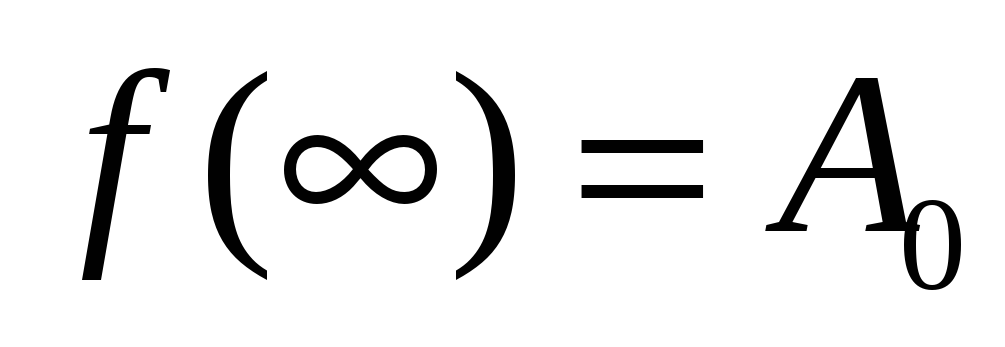(це ми приймаємо за означенням).

Безпосереднім узагальненням степеневих рядів і рядів (1), (2) є так звані ряди Лорана. Це є ряд виду

.

Збіжність ряду Лорана треба розуміти так: або що , причому і прямують до незалежно одне від одного, або, що те саме, . Тобто іншими словами, ряд Лорана збіжний тоді і тільки тоді, коли одночасно збіжні обидві його частини і .

З’ясуємо що є областю збіжності ряду Лорана. Нехай − радіус збіжності степеневої частини ряду Лорана (тобто тої частини, яка є степеневим рядом) , а − радіус збіжності іншої частини ряду Лорана . Тоді ми будемо мати, що степенева частина ряду Лорана буде збіжною в крузі і інша частина ряду Лорана буде збіжною в області . Очевидно, що якщо ці дві області не матимуть спільної частини (якщо ), то не буде жодної точки, в якій би ряд Лорана був би збіжним. Якщо ж , то ці дві області матимуть спільну частину (кільце ), яка і буде областю збіжності ряду Лорана. Це кільце може вироджуватися в круг з проколеним центром (коли ).

Якщо для ряду Лорана ми маємо, що , тобто є кільце, де ряд Лорана збіжний, то оскільки в тому кільці суми обох частин ряду Лорана є аналітичними функціями, то сума ряду Лорана теж є аналітичною функцією в тому кільці. Очевидно, як випливає з вище сказаного, ряд Лорана збігається до цієї функції рівномірно всередині кільця.

Міркуючи подібно до того, як ми це робили для степеневих рядів, можна легко одержати, що коефіцієнти ряду Лорана однозначно виражаються через суму цього ряду, а значить можна зробити відповідні висновки про єдиність представлення функції своїм рядом Лорана. Звідси можна отримати, що якщо функція парна, то вона розкладається в ряд Лорана по парних степенях, якщо непарна, то по непарних степенях.

Простий аналіз розкладу функції в степеневий ряд і того, що ми зробили зараз для ряду Лорана наводить на думку, що функцію, аналітичну в деякому кільці, можна розкласти в ряд Лорана (в степеневий ряд тут розклад не відбудеться).

Теорема. (Лорана)

Якщо функція однозначна і аналітична в кільці , то її в цьому кільці можна розкласти в ряд Лорана, тобто

, (кільце).