§3 Принцип аргументу

Нехай − деяка функція, яка аналітична в області , функція теж аналітична в цій області, за винятком хіба що полюсів, − довільне дійсне число, − замкнутий спрямлюваний контур, який повністю лежить в області разом із своєю внутрішністю і не проходить ні через полюси функції , ні через її -точки. Обчислимо такий інтеграл . Для цього розглянемо функцію . Бажаючи обчислити цей інтеграл з допомогою теореми про лишки, з’ясуємо які особливі точки має підінтегральна функція в області, що обмежується кривою і знайдемо лишки цієї функції в цих точках. З умови задачі маємо, що функція матиме у внутрішності кривої особливі точки, які будуть або -точками функції , які для функції будуть полюсами, або полюсами функції , які для функції також будуть полюсами. Нехай − -точки функції , які лежать у внутрішності кривої з відповідною кратністю і нехай - полюси функції , що лежать у внутрішності з відповідною кратністю . Ніяких більше особливих точок функція у внутрішності кривої не має. Для обчислення розкладемо функцію в ряд по степенях . Для цього порозкладаємо в ряд функції , , . Будемо мати:

,

, де ,

.

Звідси будемо мати, що

.

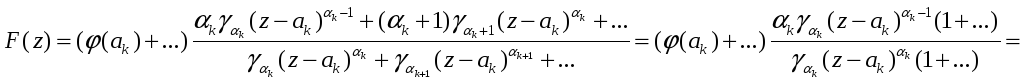
Таким чином, з тільки що одержаного маємо, що

. (1)

Обчислимо далі лишки функції відносно полюса функції . Оскільки функція аналітична в околі точки , то її розклад в ряд по степенях матиме вигляд:

.

Оскільки точка є полюсом кратності для функції , то її розклад в ряд по степенях матиме вигляд:

,

.

Тоді будемо мати для функції ,

.

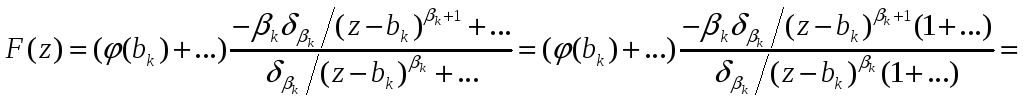
З останньої рівності видно, що

(2)

Звідси і з рівностей (1), (2) за теоремою про лишки одержимо,

.

Отже, ми отримали, що дорівнює різниці суми значень функції в -точках функції , які лежать всередині кривої , і суми значень функції в полюсах функції , які також лежать всередині кривої .

Є декілька часткових випадків одержаного твердження. Ми розглянемо один із них. Нехай . Тоді одержана вище рівність буде мати вигляд,

. (3)

Ми отримали, що інтеграл зліва в останній рівності дорівнює різниці між кількістю -точок функції , які лежать всередині кривої , і кількістю полюсів цієї ж функції, що лежать всередині кривої .

Оскільки , то ліву частину рівності (3) називають логарифмічним лишком функції .

Розглянемо частковий випадок формули (3), коли . Тоді -точки функції перетворяться в її нулі і ми можемо з рівності (3) одержати наступне:

різниця між кількістю нулів функції , що лежать всередині кривої , і кількістю полюсів цієї ж функції в тій же області буде дорівнювати логарифмічному лишку функції . Тобто

(4)

Візьмемо на кривій якусь точку і будемо рахувати її за початкову і кінцеву точку інтегрування по кривій . Якщо точка пробіжить один раз криву від точки до неї ж в додатному напрямку, то точка теж пробіжить деяку криву. Нехай − значення в початковій точці функції . А − значення , але після проходження точкою повністю кривої один раз в додатному напрямку. Оскільки під інтегралом в (4) стоїть похідна від функції , то цей інтеграл з врахуванням тільки що вказаних значень буде дорівнювати

.

Ця рівність може бути сформульована так: різниця між кількістю нулів і полюсів функції , які лежать всередині кривої , дорівнює зміні аргументу цієї функції, коли точка пробіжить один раз пробіжить криву в додатному напрямку, що ділиться на . Цей факт називають принципом аргументу.

З іншої сторони, права частина останньої рівності це не що інше як кількість обертів, які зробить навколо початку координат точка , якщо точка зробить один повний оберт по кривій . (Оберт дорівнює +1, якщо точка пробіжить один раз навколо початку координат в додатному напрямку і оберт дорівнює -1, якщо точка пробіжить один раз навколо початку координат у від’ємному напрямку ). Звідси і з принципу аргументу одержуємо, що різниця між кількістю нулів і полюсів функції , які лежать всередині кривої , дорівнює кількості обертів, які зробить вектор навколо точки 0, коли точка один раз пробіжить по кривій . Звідси, якщо функція аналітична у вказаній області , то кількість нулів цієї функції в середині кривої дорівнює кількості обертів, які зробить вектор навколо точки 0, якщо точка пробіжить один раз в додатному напрямку по кривій .

З цього результату легко одержується наступна важлива

Теорема. (Руше)

Нехай − замкнена спрямована крива, а і − функції аналітичні на кривій і у внутрішності цієї кривої. Якщо для виконується нерівність , то функції і мають всередині кривої однакову кількість нулів.