
u_lectures
.pdf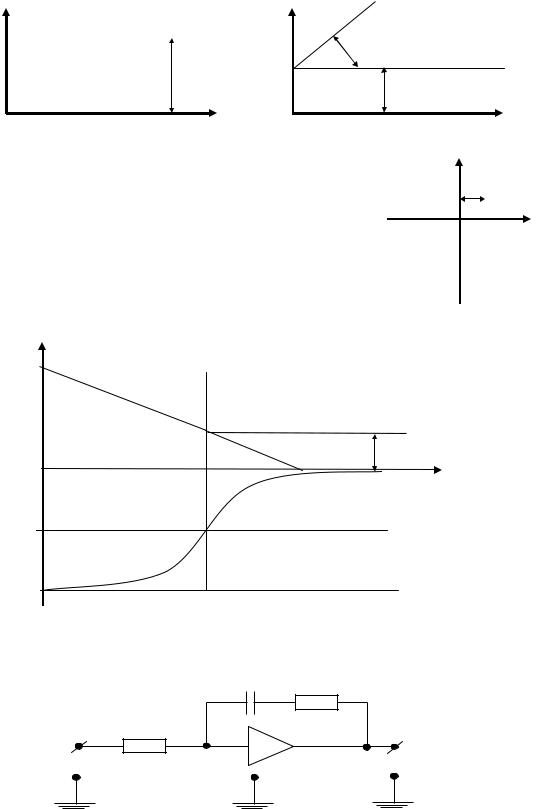
|
|
|
|
73 |
|
|
x1 |
|
|
x2 |
|
|
|
|
|
|
|
α |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
Рис. 4.44 |
|
Рис. 4.45 |
V |
||
|
|
|
||||
|
Частотные характеристики звена |
|||||
|
kT=k1 |
|||||
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
kT(Tjω+1) |
|
|
|
ω=∞ |
|
W ( jω) = |
|
|
|
ω→0 |
|
|
Tjω |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логарифмические частотные характеристики (рис. 4.47) Рис. 4.46 |
|||||
ϕ(ω) L(ω) |
|
|
1/T |
|
|
|
|
|
|
|
|
|
|
|
|
-20дБ/дек |
|
|
|
|
|
|
|
|
k 20lgk |
ω,с-1 |
|
ϕ(ω)
-45°
-90°
Рис. 4.47
Пример звена (рис. 4.48).
R2
R1 С
U1=x1 |
U2=x2 |
Рис. 4.48
Изодромное звено чаще всего применяется как регулятор, который называется также пропорционально-интегральным.
74
4.5. Дифференцирующие звенья
Их основное свойство заключается в том, что они реагируют только на изменение входного сигнала и если входной сигнал постоянный, то выходная величина равна нулю.
4.5.1. Идеальное дифференцирующее звено
Идеальное |
|
дифференцирующее звено описывается уравнением |
|
|||||
x2 = K dx1 |
dt . |
|
|
|
|
|
||
Передаточная функция звена |
|
|
|
|
|
|||
W( p ) = Kp . |
x2 |
|
|
|
||||
|
|
|
|
|
|
|
||
Переходная функция звена имеет вид |
|
h(t) |
|
|||||
|
|
|||||||
|
|
|
|
|
|
|
||
x2 = h( t ) = K d [1( t )] dt = Kδ( t ) |
|
|
t |
|
||||
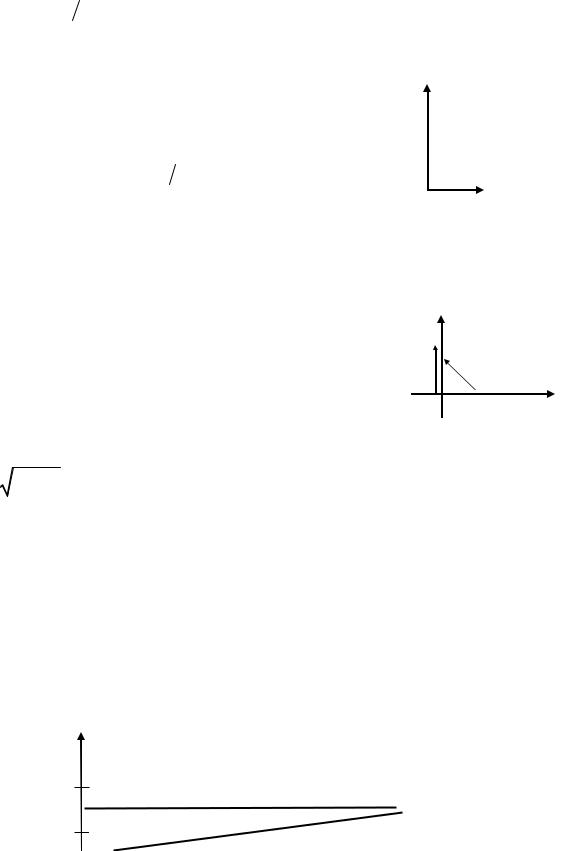
и изображена на рис. 4.49. |
|
|
|
|
||||
Рис. 4.49 |
|
|||||||
Частотная передаточная функция |
|
|
|
|
|
|||
W ( jω)=kjω , тогда U(ω)=0; |
V(ω)=kω. |
V |
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ω→∞ |
|
|
|
V (ω) |
|
|
ω |
|
|
|
|
ϕ(ω)=arctg |
|
=arctg∞=90° |
|
ϕ=90° |
U |
|||
U (ω) |
|
|
ω→0 |
|
||||
|
|
|
|
|
|
|
||
Построим ЛЧХ. |
|
|
|
|
Рис. 4.50 |
|
||
A(ω) = (kω)2 =kω L(ω) =20lgkω
Найдем наклон ЛАХ
20lgk +20lg10ω −(20lgk +20lgω) =+20дБ/дек
1)ω=1: L(ω)=20lg k
2) L(ω) =0 = 20lgkω |
ω = |
1 |
|
|
k |
Логарифмические частотные характеристики приведены на рис. 4.51.
ϕL,дБ
40 ϕ(ω)
+90°
20 |
L(ω)+20дБ/дек |
|
75
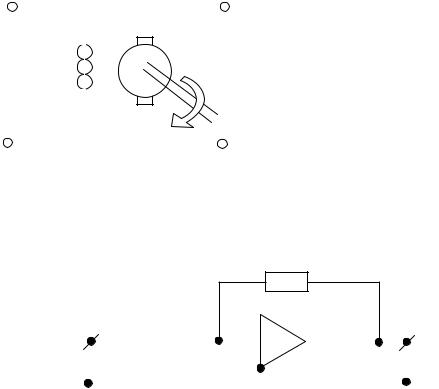
Примером звена является тахогенератор постоянного тока (рис. 4.52) в режиме холостого хода (Iя=0). При этом в качестве входной величины рассматривается угол поворота якоря, а в качестве выходной – э.д.с. якоря e.
|
|
|
|
|
|
|
|
|
|
|
|
|
Приближенно |
в |
качестве |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
идеального |
дифференциального |
|||
|
|
|
|
|
|
|
|
|
dα |
|
|||||||
|
|
|
|
|
|
|
x2=e= K |
|
|
звена |
может |
рассматриваться |
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
Uв |
|
|
|
|
|
|
|
dt |
|
|
операционный усилитель в режиме |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
дифференцирования. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
α=x1 |
|
|
Необходимо отметить, что осуще- |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ствить дифференцирование сигнала |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
реальных системах |
довольно |
||
|
Рис. 4.52 |
||||||||||||||||
|
|
|
сложно из-за наличия помех. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Приближенно в качестве идеального дифференциального звена может |
||||||||||||||||
рассматриваться операционный |
усилитель |
в |
режиме |
дифференцирования |
|||||||||||||
(рис. 4.53). |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С R
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U2=x2 |
||||||
U1=x1 |
|
|
|
|
|
||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.53
Необходимо отметить, что осуществить дифференцирование сигнала в реальных системах довольно сложно. Если x1(t) имеет разрывы первого рода, то получение точной производной невозможно.
4.5.1. Дифференцирующее звено с замедлением
Описывается уравнением
76
T dx2 +x =kT dx1 dt 2 dt
Передаточная функция
W ( p)= kTp
Tp+1
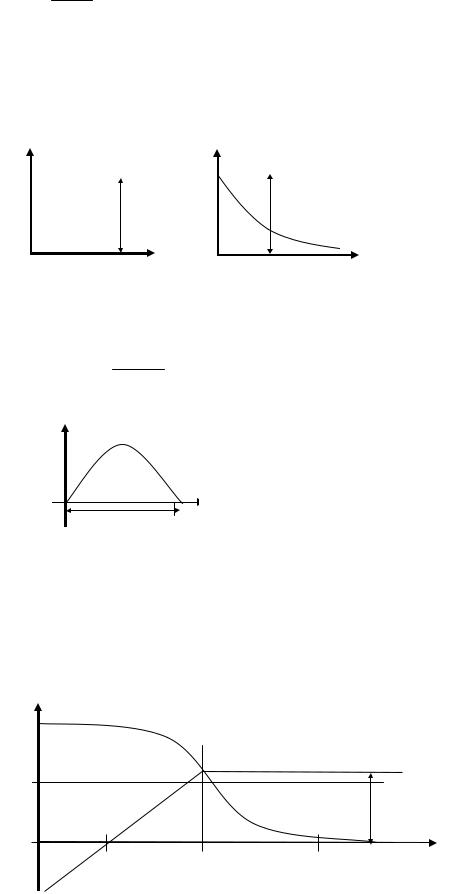
Переходная функция (рис. 4.55)
|
− |
t |
|
|
|
|
|
T |
|
|
|
||||
h(t)=ke |
|
|
|
||||
x1 |
|
|
|
x2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
k |
||
|
|
|
|
|
|
||
|
|
|
|
t |
|
|
t |
|
|
Рис. 4.54 |
|
Рис. 4.55 |
|||
Частотные характеристики
W ( jω)= kTjω
Tjω+1
V
ω=0 ω=∞
U k 

Рис. 4.56
Логарифмические частотные характеристики (рис. 4.57).
ϕ(ω) L(ω)
+90°
+45°
20lgk
ω,с-1
1 |
1/T |
10 |
+20
Рис. 4.57

77
Примеры:
С
U1=x1 R 
 U2=x2
U2=x2
Рис. 4.58 |
Рис. 4.59 |
|
z = |
|
1 |
|
|
z =R |
|
|
|
|
|
||||||||
Cp |
|
|
|
|
|
|||||||||||||
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||
U |
|
= |
|
z2 |
U = |
|
R |
U = |
RCp |
U |
||||||||
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
z1 +z2 |
1 |
|
|
|
|
|
1 |
1 |
RCp+1 |
1 |
|||
|
|
|
|
|
|
|
|
|
R+Cp |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
W = |
|
RCp |
|
= |
|
Tp |
, |
|
k=1. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
RCp+1 Tp+1 |
|
|
|
|
|
|||||||||
Выше рассмотрены типовые линейные звенья, которые наиболее часто встречаются в системах управления, но в некоторых САУ встречаются и другие типы звеньев, например:
1) неминимально-фазовые устойчивые звенья (имеют нули в правой полуплоскости), 2) неустойчивые звенья (имеют полюсы в правой полуплоскости)
W( p)=Tpk−1,
3)звенья с распределенными параметрами, которые делятся на:
•иррациональные и описываются иррациональными функциями;
W ( p)= |
k |
; |
W ( p) = |
|
k |
|
; |
p |
+ |
|
|||||
|
|
|
|
1 |
pT |
||
78
•трансцендентные, описываемые трансцендентными функциями; например,
W ( p)=e−pτ - звено чистого запаздывания.
7. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ САУ
Переходный процесс САУ – это закон изменения ее выходной координаты после внезапного изменения сигнала на входе. В качестве входных воздействий наиболее часто встречаются следующие: δ(t); 1(t);
−t
sin(ω t); tk– степенная функция; e T – показательная функция.
Переходная функция h(t) – частный случай переходного процесса для xвx =1(t).
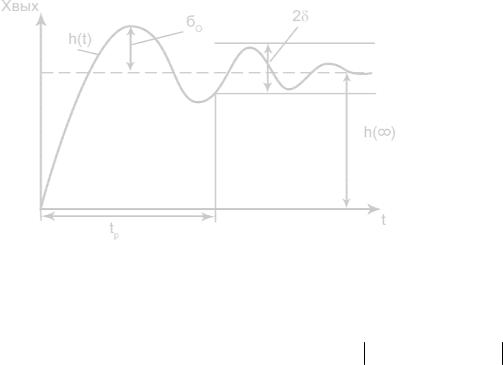
Рис. 7.1
На рис. 7.1,а изображена система автоматического управления и возможные типы переходных процессов рис. 7.1,б.
Существует ряд методов для расчета переходных процессов.
1.Классический метод решения дифференциальных уравнений, которые описывают замкнутую систему.
2.Операторный метод решения дифференциальных уравнений.
3.Частотный метод построения переходных процессов.
Методы 1 и 2 применяются для дифференциальных уравнений не выше третьего порядка. Метод 3 – приближенный и применим для устойчивых систем любого порядка, причем рост порядка уравнения мало сказывается на трудоемкости расчетов.
4. Графические методы.
Используются для построения переходных процессов в нелинейных системах.
5.Метод расчета переходных процессов на АВМ.
6.Метод расчета на ЦВМ путем интегрирования систем дифференциальных уравнений методом Рунге-Кутта.
Разработаны эффективные и удобные пакеты программ для решения этой задачи, например, Matlab.
7.1.Операторный метод решения дифференциальных уравнений

79
Пусть имеем систему автоматического управления (рис. 7,а) и известен закон изменения входной величины xвx (t), по которому можно определить
изображение Xвх(p).
Найдем изображение выходной величины
Хвых(p)=W (p) Хвх (p)= |
B(p) |
. |
|
||
|
A(p) |
|
Тогда при отсутствии нулевых и кратных корней можно найти оригинал
|
B(0) |
n |
|
B( pi ) |
e pi t , |
|
xвых(t) = |
+ ∑ |
|
(7.1) |
|||
A(0) |
p |
|
||||
|
i=1 |
A′( p ) |
|
|||
|
|
|
i |
i |
|
|
где n – число корней характеристического уравнения системы, т.е.
A(p)=0;
A′( p) = dAdp( p) ,
pi – значение i-го корня.
Здесь трудоемко только вычисление корней (при решении дифференциальных уравнений необходимо дополнительно вычислять постоянные интегрирования Ci).
7.2. Частотный метод расчета переходных процессов
Метод применяется для устойчивых систем любого порядка. Пусть передаточная функция замкнутой системы имеет вид
W ( p) = Хвых ( p)
Хвх ( p)
Если перейти к частотной передаточной функции
W ( jω) = P(ω) + jQ(ω),
то можно получить выражение для переходной функции
|
2 |
∞ |
sinωt |
|
|
||
h(t) = |
|
|
∫P(ω) |
|
dω . |
(7.2) |
|
π |
ω |
||||||
|
0 |
|
|
||||
|
|
|
|
|
|
||
Выражение (7.2) является основой частотного метода и позволяет определить переходную функцию, то есть реакцию САУ на единичную
80
ступенчатую функцию. Это выражение аналитически вычисляется сложно, поэтому применяют приближенные или численные методы вычисления интеграла на ЭВМ.
8. КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
Необходимым условием работоспособности системы является ее устойчивость. Но устойчивая система может обладать недостаточным быстродействием, точностью, то есть качество работы системы может не соответствовать требованиям, которые предъявляются конкретным технологическим процессом. Для количественной оценки качества регулирования вводят показатели качества.
8.1. Оценка качества по переходной функции
Оценка широко применяется из-за простоты и наглядности эксперимента, как на модели, так и в реальных условиях.
Если xвх =1(t) , то на выходе системы получим переходную функцию
h(t).
Рис. 8.1
Имея h(t) можно определить следующие показатели качества. 1)Быстродействие определяется временем регулирования tp. Время
регулирования – это время от момента подачи входного воздействия до момента, после которого выполняется неравенство xвых (t) − xвых (∞) < δ , где
δ – заданная малая постоянная величина, которая является заданной точностью системы. Часто принимают δ = 5% .
2) Перерегулирование σ0 – это максимальный выброс регулируемой величины относительно установившегося значения. Перерегулирование

|
|
81 |
|
σ% = |
σ0 |
100% – это относительная величина. Она характеризует |
|
xвых (∞) |
|||
|
|
склонность системы к колебаниям.
3) Статическая ошибка или установившееся рассогласование
xуст = xвх − xвых (∞) .
Рис. 8.2
4) Динамическая ошибка x(t) = xвх (t) − xвых (t).
Оценка качества по h(t) является прямым способом оценки качества. Однако для линейных систем эта задача успешно решается и косвенными методами.
8.2. Косвенные методы оценки качества
Эти методы делятся на три группы:
–частотные;
–интегральные;
–корневые.
1. Частотные способы оценки качества.
При исследовании системы с помощью частотных характеристик используют такие параметры, как запас устойчивости по модулю и запас устойчивости по фазе.
Запас устойчивости по модулю – это величина, которая показывает во сколько раз нужно увеличить заданный коэффициент усиления (при неизменных других параметрах), чтобы устойчивая система оказалась на границе устойчивости
K = Kкр , K з
где Kкр – критический коэффициент усиления, при котором система находится на границе устойчивости,
Kз – заданный коэффициент.

82
|
V |
|
–1 |
ω=0 |
U |
|
КЗ
аWР(jω) Wp(p)ККР
|
|
|
|
|
Рис. 8.3 |
|
|
Пусть ω |
|
– частота, при которой ϕ = −180o , тогда |
|
||||
1 |
|
|
|
|
|
|
|
Wр ( jω) = U (ω) + jV (ω) = K[U1 |
(ω) + jV1 (ω)] = KU1 (ω1 ) |
(8.1) |
|||||
|
|
|
|
|
|
123 |
|
Из выражения (8.1) следует, что |
=0 |
|
|||||
|
|
||||||
K з U1 (ω1 ) = −a , |
|
(8.2) |
|||||
Kкр U1 (ω1 ) = −1. |
|
(8.3) |
|||||
Из (8.2) и (8.3) найдем |
|
|
|||||
K = |
Kкр |
= |
1 |
>1. |
|
(8.4) |
|
|
K з |
a |
|
||||
|
|
|
|
|
|
||
Запас устойчивости по фазе – это величина, которая показывает насколько нужно увеличить (или уменьшить) фазу, чтобы устойчивая
система оказалась на границе устойчивости (при постоянстве других |
|||
параметров). |
|
V |
|
|
|
|
|
|
|
a |
|
|
–1 |
ω = ∞ |
U |
|
|
||
|
γ |
|
|
|
|
|
|
|
|
φ1 |
|
Рис. 8.4
