
u_lectures
.pdf
163
Перейдем к эквивалентной схеме. Функция, описывающая форму импульса, представлена на рис. 18.8,б. Найдем передаточную функцию формирующего звена.
∞ |
T |
1− e− pT |
|
|
Wф(p)= ∫1 e−pt dt = ∫e−pt dt = |
|
. |
||
p |
||||
0 |
0 |
|
||

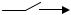 WФ(p)
WФ(p)  WН(p)
WН(p)  -
- 
Рис. 18.9
Представим передаточную функцию в виде сомножителей
Wф(p)= (1 − e−pT ) |
1 |
|
= W ( p) W |
( p) . |
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
Т |
|
|
|
Ф.Н.Ч. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
WТ(p) |
|
|
|
|
|
|
|
WП.Н.Ч.(p) |
|
|
|
|||||||
- |
|
|
|
|
|
|
|
1-e-pT |
|
|
|
|
|
|
|
|
|
k |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(T1p+1) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.10 |
|
|||
WП.Н.Ч.(p)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p(T p +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Разлагаем на простые дроби |
|
|
|
||||||||||||||||||||||||
|
k |
= |
A |
|
+ |
|
|
|
B |
|
|
|
|
= |
|
AT1 p + A + Bp |
|
A = k; B = -kT1; |
|||||||||
|
p(T p +1) |
p |
T p +1 |
|
|
p(T p +1) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
k |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
= k |
|
− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
p(T1 p +1) |
p |
|
+ |
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
|
|
||||||||||
По таблице дискретного преобразования Лапласа [1] находим:
* |
|
e pT |
|
|
|
e pT |
|
|
|
|
e pT (1 − e−T / T1 ) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
= k |
|
|
|
|
|
|
|
|
|
|
pT |
|
|
− |
pT |
|
−T / T |
|
pT |
|
−T / T |
pT |
. |
|||||
WП.Н.Ч. ( p) = k |
−1 |
− e |
|
(e |
− e |
||||||||||||||
|
e |
|
|
e |
|
1 |
|
|
|
1 )(e |
|
−1) |
|||||||
Передаточная функция разомкнутой системы
164
W * ( p) =W ( p) W * |
( p) = (1−e− pT ) k |
epT (1−e−T /T1 ) |
|
= |
|||||
|
|
||||||||
p |
|
|
T |
П.Н.Ч. |
|
(epT −e−T /T1 )(epT |
−1) . |
||
|
k(1 |
−e |
−T /T1 |
|
|
||||
= |
|
) |
|
|
|
|
|
||
pT |
−e |
−T /T |
|
|
|
|
|
||
|
e |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Таким образом, Wp*(p) является трансцендентной функцией и может быть представлена в виде отношения двух полиномов.
18.3. Передаточные функции замкнутых систем
Для частного, но наиболее распространенного способа включения ИЗ в САУ после сумматора, эквивалентная схема представлена на рис. 18.11.
xвх |
x |
x* |
|
xвых |
|
Wфн(p) |
|||||
|
- |
|
|
||
|
|
|
|
Рис. 18.11
Схему можно преобразовать (рис. 18.12 и рис. 18.13)
xвх |
x*вх |
|
|
xвых |
x*вых x*вх |
|
|
|
x*вых |
|
W (p) |
|
* |
(p) |
|||||
|
|
- |
фн |
|
|
- |
Wp |
|
|
|
|
Wp* (p) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
Рис. 18.12 |
|
|
|
Рис. 18.13 |
|||
Передаточная функция замкнутой системы для схемы на рис.18.13 находится также как и для непрерывной системы:
* |
|
X вых* ( p) |
|
Wp* ( p) |
|
|
|
|||||||
W (p) = |
|
|
|
|
= |
|
|
|
|
Пусть |
||||
|
|
X вх* ( p) |
|
1+Wp* ( p) |
|
|
|
|||||||
Wp*(p) = |
B* ( p) |
, тогда |
|
|
|
|
|
|
||||||
C* ( p) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B* ( p) |
C* ( p) |
|
|
B* ( p) |
|
B* ( p) |
|
|||
* |
|
|
|
|
|
= |
|
= |
|
|||||
W (p) = |
|
|
|
|
|
|
, |
|||||||
1 |
+ B* ( p) |
|
C* ( p) + B* ( p) |
A* ( p) |
||||||||||
|
|
|
|
|
|
|
C* ( p) |
|
|
|
|
|
|
|
165
где A*(p) = C*(p)+ B*(p)=a0enpT+ a1e(n-1)pT+…+ an –
–характеристический полином замкнутой системы.
Вобщем случае для импульсных САУ при нахождении передаточных функций необходимо учитывать взаимное расположение непрерывных и импульсных элементов.
Вначале рассмотрим три случая расположения ИИЗ в разомкнутых
системах. |
|
|
|
|
|
ИИЗ |
1) |
|
|
|
|
|
|
x*вх |
|
|
|
|
x*вых |
|
xвх |
|
|
|
|
xвых |
|
W1(p) |
|
W2 (p) |
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 18.14 |
|
||
Изображение выходного сигнала имеет вид |
|
|||||
X*вых(p) = X*вх(p)W1W2*(p), где обозначено
W1W2*(p) = Z[W1(p)W2 (p)], то есть W*p(p) = W1W2*(p).
2) Пусть два звена с передаточными функциями W1(p) и W2 (p) соединены последовательно и разделены двумя ИИЗ, которые работают
синхронно. |
|
|
|
ИИЗ2 * |
|
|
|
|
x*вых(t) |
||||||
|
ИИЗ1* |
|
|
|
|
|
|
|
|||||||
xвх |
|
x вх |
|
W1(p) |
x1(t) |
|
x1 (t) |
|
W2 |
(p) |
|
xвых(t) |
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.15 |
|
|
|
|||
Для схемы (рис. 18.15) запишем |
|
|
|
|
|
||||||||||
X*1(p) = X*вх(p)·W1*(p) |
, где |
W1*(p) = Z[W1(p)]; |
|
||||||||||||
X*вых(p) = X*1(p)·W2*(p) |
, где |
W2*(p) = Z[W2(p)]; |
|
||||||||||||
X*вых(p) = W2*(p)·W1*(p)·X*вх(p) = W*p(p)·X*вх(p) |
|
||||||||||||||
W*p(p) = W2*(p) ·W1*(p) |
|
|
|
|
|
|
|
|
|
||||||
В общем случае W1W2*(p)≠ W1*(p) ·W2*(p) |
|
|
|
||||||||||||
3) |
|
|
|
|
|
ИИЗ x1* |
|
|
|
|
|
|
|
x*вых |
|
xвх |
|
|
|
|
x1 |
|
|
|
|
|
|
|
xвых |
||
|
W1(p) |
|
|
W2 (p) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.16
Для схемы найдем изображение выходного сигнала
X*вых(p) = X*1(p) ·W2*(p), где X*1(p) = Z[Xвх(p)W1 (p)]= XвхW1*(p)

167
xвх |
x |
|
x1 |
x1* |
|
xвых |
W1(p) |
W2(p) |
|||||
|
– |
|
|
|
|
* |
|
|
|
|
|
|
x вых |
Рис. 18.18
Составим уравнения для отдельных элементов схемы
X1(p) = X(p)W1(p)= W1(p) [Xвх(p) – Xвых(p)]= =W1(p)Xвх(p)- W1(p)W2(p)X*1(p).
Применим к этому равенству дискретное преобразование
X*1(p)= XвхW*1(p) – W1W*2(p)X*1(p),
где XвхW*1(p) = Z[Xвх(p)W1(p)], W1W*2(p) = Z[W1(p)W2(p)].
Из выражения получим
* |
|
X W * ( p) |
||
|
вх |
1 |
|
|
X |
1(p) = |
|
. |
|
1+W W * ( p) |
||||
|
|
1 |
2 |
|
Окончательно изображение выходной величины
X * |
( p) = X * ( p)W * ( p) = |
XвхW1* ( p) W2* ( p) |
, |
||
1+W W * ( p) |
|||||
вых |
1 2 |
|
|||
|
|
1 |
2 |
|
|
где W*2(p) = Z[W2(p)].
То есть передаточная функция в явном виде не выражается.
19. УСТОЙЧИВОСТЬ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
19.1. Понятие об устойчивости
Линейная импульсная САУ считается устойчивой, если после
кратковременного внешнего воздействия |
(например, xвх(t)=δ(t)) при t → |
∞ xвых(t) → 0. |
|
Пусть W*(p) = B* ( p) – передаточная функция замкнутой системы.
A* ( p)
Тогда характеристический полином замкнутой системы |
|
A*(p) = C*(p)+ B*(p)=a0enpT+ a1e(n-1)pT+…+ an . |
(19.1) |
Корни характеристического уравнения рассматриваются в полосе
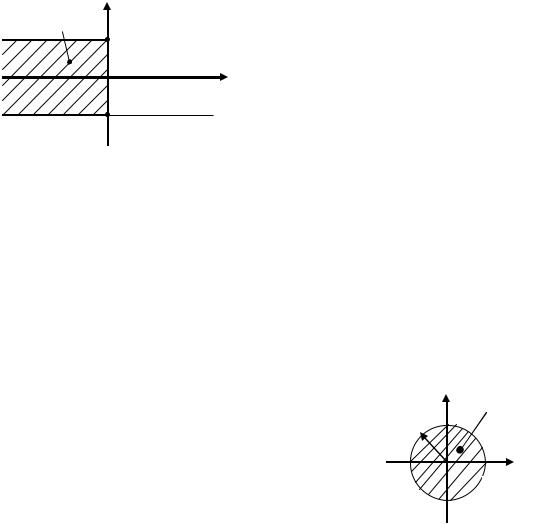
|
|
|
|
|
|
|
169 |
|
v = |
z −1 |
= |
e pT −1 |
. |
(19.7) |
|||
|
|
|
|
|||||
z +1 |
e pT +1 |
|||||||
|
|
|
|
|||||
Из (19.7) видно, что если вещественная часть комплекса vi = αv +jβv будет отрицательна, то |zi| < 1 и система устойчива. Характеристическое
уравнение принимает вид |
|
|
|
|
|
1+v n |
1 |
+v n−1 |
(19.8) |
A(v) = a0 |
+ a1 |
|
+…+ an =0 |
|
|
1−v |
1 |
−v |
|
или |
|
|
|
|
a0 (1+v)n + a1 (1+ v)n−1 (1−v) +…+ an (1−v)n =0, |
|
|||
a0’ vn + a1’ vn−1 +…+ an’ =0, |
(19.9) |
|||
где – a0’, … an’ – новые коэффициенты.
Для характеристического уравнения (19.3) можно использовать критерий Гурвица, сформулированный для непрерывных систем, и исследовать систему на устойчивость.
19.3. Критерий устойчивости Михайлова для импульсных систем
Пусть имеем характеристический полином замкнутой системы.
A(z) = a0zn+ a1zn-1 +…+ an , |
(19.9) |
где z = epT. |
|
Разложим (19.9) на сомножители |
|
A(z) = a0(z –z1)(z –z2)…(z –zn), |
(19.10) |
где zi – корни уравнения A(z)=0, соответствующие корням pi характеристического уравнения A*(p)=0.
Положим z = ejωT и найдем изменение аргумента (фазовый сдвиг) одного из сомножителей (z –zi), входящих в состав A(z),
jωT |
|
|
|
ωи |
ωи |
|
|
arg (e |
-zi) |
при изменении − 2 < ω ≤ |
2 . |
|
|
||
|
|
|
|
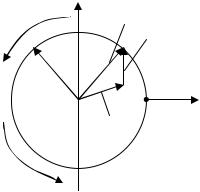
1) Допустим |zi| |
< 1, |
что |
|
|
|
|
e |
соответствует корню pi = αi ± jβi |
при αi |
||
|
|
|
|
< 0. |
|
|
|
ω |
|
|
ω |
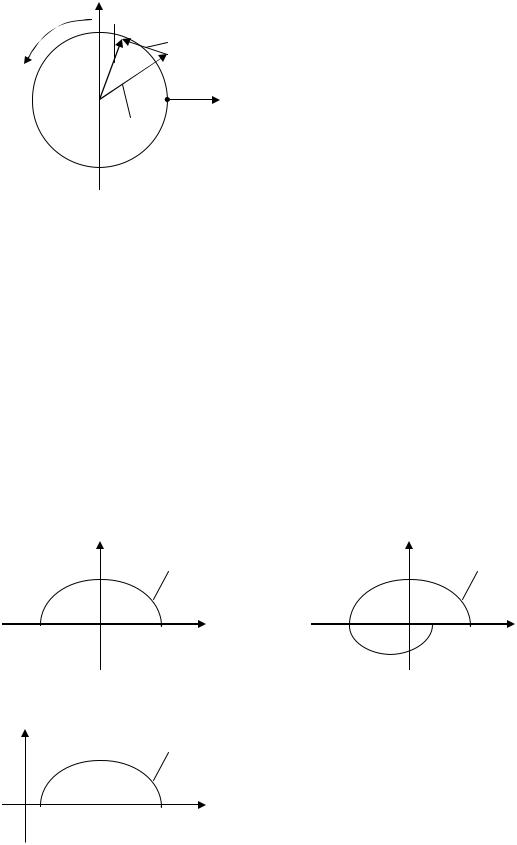
Концы |
векторов |
скользят |
по |
|
|
окружности единичного радиуса. |
|
||||
|
|
|
|
|
|||
Рис. 19.3
171
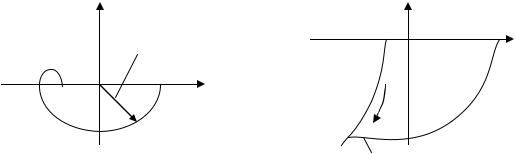
19.4. Критерий устойчивости Найквиста для импульсных систем
Пусть разомкнутая система устойчива или нейтральна и имеет передаточную функцию Wp*(p).
Замкнутая система будет устойчива, если при изменении ω от 0 до ωи/2 годограф вектора Wp*( jω) не охватывает точку (-1, j0).
Система устойчива в |
Для нейтральной |
|
системы |
||
замкнутом состоянии |
||
|
||
W |
|
|
ω |
|
Дополнение годографа |
Рис. 19.6 |
к бесконечности |
|
а б
Рис.
20. КОРРЕКЦИЯ ИМПУЛЬСНЫХ СИСТЕМ
20.1 Способы коррекции
Вобщем случае для достижения требуемых показателей качества переходных процессов вводят корректирующие устройства.
Вотличие от непрерывных систем применяют два способа коррекции: непрерывный и импульсный.
172
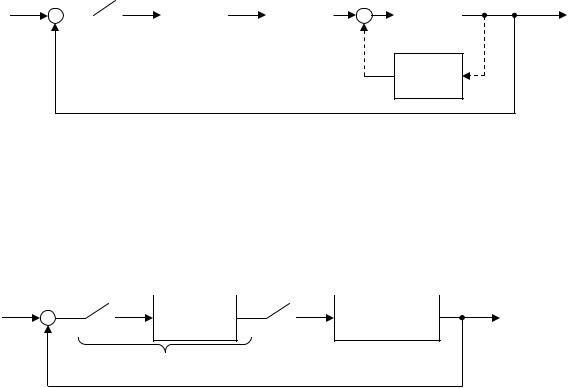
При первом способе коррекция осуществляется введением непрерывных корректирующих устройств, при втором – введением в
систему импульсных и цифровых фильтров.
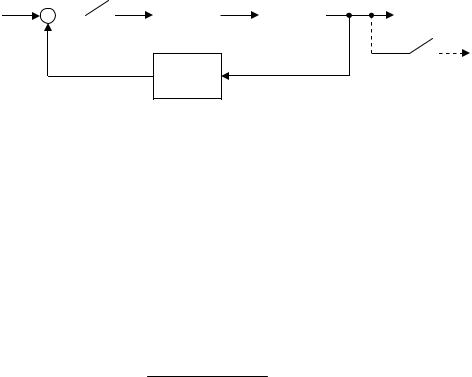
1. При непрерывной коррекции непрерывное корректирующее звено вводят последовательно или параллельно с элементами непрерывной части.
.
xвх |
|
|
|
|
|
|
|
xвых |
|
|
WФ(p) |
|
WК1(p) |
|
WН(p) |
||
- |
|
|
|
|
|
- |
|
|
WК2(p)
Рис. 20.1
При этом деформируются частотные характеристики приведенной непрерывной части. Задачу решают методом ЛЧХ.
2. Импульсная коррекция состоит во введении в импульсную систему импульсного фильтра.
|
|
|
|
xвых |
|
WФ1WК |
|
WФ(p)WН(p) |
|
xвх |
|
|
|
|
-
WК*(p)
Рис. 20.2
Импульсный элемент преобразует дискретные значения входного сигнала в последовательность импульсов.
Обычно в процессе синтеза получают передаточную функцию WК*(p) в виде импульсной передаточной функции, затем определяют передаточную функцию WК(p).
3.Использование цифровых фильтров.
Вэтом случае по импульсной передаточной функции WК*(p) находят разностное уравнение и решают его на ЦВМ.
