
u_lectures
.pdf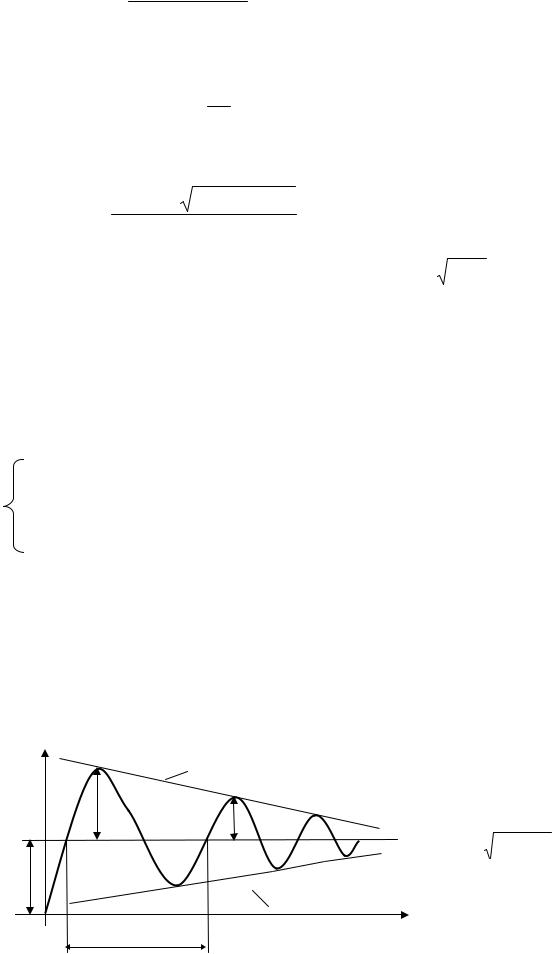
63
k |
|
|
W ( p) = T 2 p2 + 2ξTp +1, |
||
где T = T2 , 2ξT = T1 . |
|
|
Откуда определим ξ = |
T1 |
< 1 - показатель колебательности. |
|
2T |
|
Корни характеристического уравнения будут равны
r |
= |
− 2ξT ± 4ξ2T 2 |
− 4T |
2 |
|
|
|
||
|
|
=α ± jβ, |
|
|
|
||||
1,2 |
|
|
2T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где α = − |
ξ |
|
– вещественная |
часть корней; β = |
1 |
1−ξ 2 |
– мнимая часть |
||
T |
T |
||||||||
|
|
|
|
|
|
||||
корней.
Если на вход поступает воздействие x1=1(t), то найдем переходной процесс. x*2=k;
x2 =[k+eαt (C1cos βt+C2 sin βt)]1(t)
Пусть при t=0; (x2)0=0 и (x΄2`)0=0
(x2)0 =k +C1 =0 |
C1 =−k |
|
|
||
(x2′)0 =αC1 +βC2 =0 |
C2 |
=− |
αC1 |
= |
αk |
|
|
|
β |
|
β |
x2 = h(t) = K[1 − eαt (cos βt − αβ sin βt)] 1(t).
Переходный процесс изображен на рис. 4.15. На основе полученной переходной функции можно определить параметры передаточной функции.
|
|
|
Из рис. 4.15 следует: |
|||||||||
x2 |
k(1+eαt) |
|
2π |
1 |
|
|
|
A |
||||
|
|
|
β = |
|
; α = |
|
|
ln |
2 |
; |
||
|
h(t) |
|
τ |
τ |
A |
|||||||
|
A2 |
|
|
|
|
|
|
|
|
1 |
|
|
A1 |
|
α2 +β 2 = |
1 |
|
|
|
||||||
|
|
|
но |
|
, тогда |
|||||||
|
|
|
T |
|||||||||
K |
|
получим |
|
|
|
|
|
|||||
k(1-eαt) |
|
|
|
|
|
|
|
|||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
τ=2π/β |
|
|
|
|
|
|
|
|
|
|
|
64
Т= |
1 |
; ξ = −αT . |
|
α 2 + β 2 |
|||
|
|
Рис. 4.15
Частотные характеристики
W ( jω) = |
|
|
k |
2 |
2 |
+2ξTjω+1 |
|
|
−T ω |
|
Логарифмические частотные характеристики
W ( jω) = |
k |
= |
(1−T 2ω2 )+ j2ξTω |
= |
k |
|
× |
A− jB |
= |
|
kA |
|
− j |
kB |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
2 |
2 |
+B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A+ jB A− jB |
|
A +B |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
V(ω) |
|
|
|
|
|
где обозначено А=1–Т2ω2; |
В= 2ξТω. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
Найдем модуль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ω= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2(A2 +B2 ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ω=0 |
U(ω) |
A(ω) = |
|
kA |
2 |
+( |
kB |
|
2 |
= |
|
= |
|
k |
|||||||||||
2ξ |
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
A2 +B2 |
|
A2 +B2 |
|
|
(A2 +B2 )2 |
|
A2 |
|||||||||||||||||
k |
|
|
|
|
ω=1/T |
|
|
|
A(ω) = |
|
|
|
k |
|
|
|
|
= |
|
|
|
|
|
k |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(1−T 2ω2 )2 +4ξ2T 2ω2 |
2 ( |
1 |
−ω2 )2 +4ξ2ω |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65
Тогда ЛЧХ будут иметь вид:
L(ω) =20lgk −20lgT 2 ( |
1 |
|
−ω |
2 )2 +4ξ2ω2 |
|
1 |
|
|
|
|
|||
T 2 |
T 2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
ϕ(ω) =arctg |
V (ω) |
=arctg(− |
kB |
) =−arctg( |
|
2ξTω |
|
||||||
|
|
|
|
|
) . |
|
|||||||
U(ω) |
kA |
|
|
2 2 |
|
||||||||
|
|
|
|
1−T |
ω |
|
|||||||
Построим ЛЧХ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) ω<1/T, то ω2≈0, L(ω)=20lg k |
|
|
|
|
|
|
|||||||
2)ω>1/T, то 1/T2≈0, L(ω) = 20lg k − 20lgT |
2ω |
2 = L (ω) + L (ω) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
Наклон L (ω) |
−20lgT 2102ω2 −(−20lgT 2ω2) =−20lg102 =−40дБ/дек |
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛЧХ изображены на рис. 4.17 при различных значениях ξ.
|
ϕ L,дБ |
|
|
|
|
ω=Т-1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ξ=0,01 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ=0,1 |
|
|
|
|||
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-40дБ/дек |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
20lgk |
|
|
|
|
|
ξ=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L(ω) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
1 |
|
|
|
|
|
ω,с-1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|||||||||||||
-90° |
|
|
|
|
|
|
|
|
ϕ(ω) |
|
|
|
|
ξ=1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
ξ=0,1 |
ξ=0,01 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
-180° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.17 |
|
|
|
|
|
|||||
|
Фазовые характеристики звена могут быть построены по выражению |
||||||||||||||||||||||||
ϕ(ω) = −arctg |
|
2εТ1ω |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
−Т1 ω |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

66
При вычислении характеристики φ(ω) на калькуляторе или в системе Mathcad необходимо учесть переход с одной ветви функции arctg на другую при изменении знака знаменателя и проводить вычисления по выражениям:
|
2εТ1ω |
|
|
|
1 |
|
|
|||
−arctg |
|
|
|
, |
при ω ≤ |
|
|
|
|
; |
2 |
|
2 |
T1 |
|||||||
|
1−Т1 ω |
|
|
|
|
|||||
ϕ(ω) = |
|
|
2εТ1ω |
|
1 |
|
|
|
||
−180o −arctg |
|
, при ω > |
. |
|
||||||
|
|
|
|
|||||||
|
1−Т2ω2 |
|
T1 |
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
Примеры колебательных звеньев.
1. Двигатель постоянного тока с независимым возбуждением (рис. 4.18).
Uв |
Uя=x1 |
ω=x2
Рис. 4.18
Описывается |
уравнением |
в |
операторной форме |
|
|
(TМTЯp2+TМp+1)ω=КДUЯ,
где TЯ=LЯ/RЯ – электромагнитная постоянная якоря; TM=(RЯJ)/(CЕCМ) – электромеханическая постоянная; КД=1/CЕ – коэффициент передачи двигателя.
2. RLC–цепь (рис. 4.19) |
|
|
|
|||||
|
|
R |
|
|
L |
|
Описывается уравнением |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(LCp2+RCp+1)U2 =U1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звено является колебательным при |
|
|
|
|
|
|
||||
u1 |
|
|
|
С |
u2 |
|||
|
|
|
|
|
|
|
выполнении условияR < 2 |
L . |
|
|
|
|
|
|
|
|
C |
|
|
|
Рис. 4.19 |
|
|
|
||
4.3.2.Апериодическое звено второго порядка
Вэтом случае передаточная функция звена второго порядка
67
W ( p) = |
|
k |
|
T 2 p2 |
+T p +1 |
|
|
2 |
1 |
|
|
записывается в более удобной форме
W ( p) = |
|
k |
|
|
. |
||
(T p +1)(T p +1) |
|||
|
3 |
4 |
|
Постоянные времени Т3 и Т4 определяют из решения системы уравнений
T22 = T3T4 ,
T1 = T3 +T4 ,
и их значения равны
T |
= |
T |
± |
T 2 |
−T |
2 |
. |
1 |
1 |
|
|||||
3,4 |
|
2 |
|
4 |
2 |
|
|
|
|
|
|
|
|
||
Апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно с общим коэффициентом k и постоянными времени T3 и T4.
Переходная функция находится путем решения дифференциального уравнения. Характеристическое уравнение звена имеет действительные отрицательные корни.
(T3r+1) (T4r+1)=0; |
r1= –1/T3, |
r2= –1/T4 . |
|||
Если x1=1(t), то |
x = h(t) = k +C er1t |
+C |
2 |
er2t . |
|
|
2 |
1 |
|
|
|
C1 и C2 найдем с учетом начальных условий: t=0, x2= x2`=0.
(x1)0 =k +C1 +C2 =0 |
C = |
r1k |
; |
C = |
r2k |
; |
|
|
|||||
(x2′)0 =r1C1 +r2C2 =0 |
2 r2 −r1 |
1 r2 −r1 |
||||
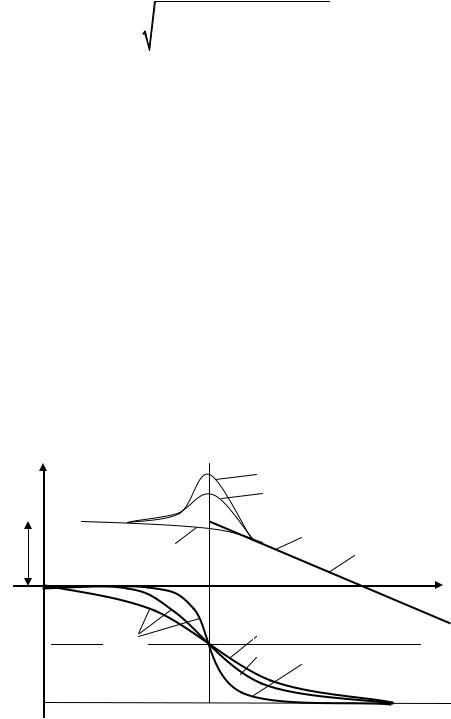
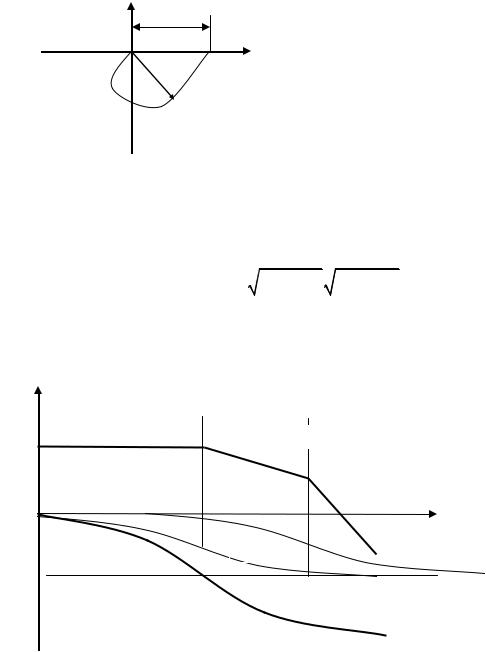
Переходная функция изображена на рис. 4.20.
T3+T4
x1 |
x2 |
1 |
|
|
|
h(t) |
K |
|
|
|
|
||
|
|
|
|
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
Рис. 4.20 |
|
T4 |
|
|
|
|
|
|
68
Частотная передаточная функция имеет вид
W ( jω)= |
|
k |
(T |
jω+1)(T jω+1) |
|
3 |
4 |
|
АФХ изображена на рис. 4.21.
V
ω= |
k |
U |
|
||
|
|
|
|
A(ω) |
ω=0 |
|
|
Рис. 4.21
Логарифмические частотные характеристики (рис. 4.22), построены по выражениям
L(ω) = 20lg A(ω) = 20lg |
|
k |
|
|
; |
T 2ω2 |
+1 |
T 2ω2 |
+1 |
||
|
3 |
|
4 |
|
|
ϕ(ω ) = ϕ3 (ω ) +ϕ4 (ω ) = −arctgT3ω − arctgT4ω .
ϕ L,дБ |
|
1/T3 |
|
1/T4 |
||||
|
|
|
40 |
|
L(ω) |
|
-20дБ/дек |
|
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
20 |
|
|
|||
|
|
|
|
|
|
|
-40дБ/дек |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω,с-1 |
|
|
|
|
|
|
|
|
ϕ4 |
|
|
|
|
|
|
|
ϕ3 |
|
-90° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ(ω) |
-180° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 4.22
Примеры апериодических звеньев второго порядка.
69
1. Двигатель постоянного тока при выполнении условия TМ ≥4TЯ.
2. RLC–цепь при выполнении условия R ≥ 2 L C .
4.4. Интегрирующие звенья
Общее свойство интегрирующих звеньев в том, что их выходная величена неограниченно возрастает при постоянной величине входного сигнала.
4.4.1. Идеальное интегрирующее звено
Описывается уравнением
dxdt2 =kx1 ,
и имеет передаточную функцию
W( p ) = kp .
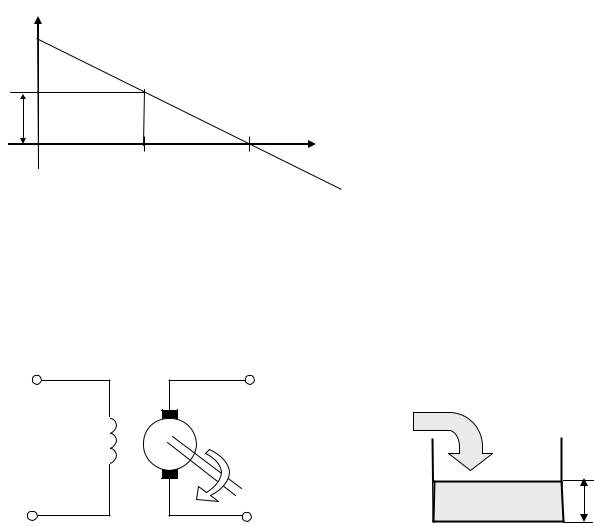
Переходная функция: x1(t) =1(t);
x1
1
x2(t) =h(t) =k t∫1(t)dt =kt .
0
x2
|
|
tgα=k |
|
|
α |
||
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.33 |
|
|
|
Частотная передаточная функция |
|
V |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( jω) = |
|
k |
|
|
=− j |
|
k |
|
; U(ω)=0; V(ω)= - k/ω |
|
|
|
||||
|
jω |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
ω |
|
|
ω=∞ |
U |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(ω) = |
(− |
|
k |
|
) |
2 |
= |
|
k |
: |
ω |
W(jω) |
|
|||
ω |
|
|
ω |
|
ω→0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
ϕ(ω) =arctgU(ω) =arctg(−∞) =−90° |
|
|
||||||||||||||
Рис. 4.34 |
|
|||||||||||||||
|
|
|
|
|
V (ω) |
|
|
|
||||||||
70
Логарифмические частотные характеристики (рис. 4.35) строятся по выражениям
L(ω) = 20lg k − 20lgω; |
ϕ(ω ) = −90o . |
|
|||
L(ω) |
|
|
|
|
|
|
|
|
|
Если ω=1, то L(ω)=20lg k . |
|
|
|
|
|
Найдем наклон. |
|
20lgk |
|
|
|
20lg k − 20lg10ω − (20lg k − 20lgω) = |
|
|
k=ω |
ω,с-1 |
|||
|
|
||||
|
|
|
= −20дБ / дек |
||
1 |
10 |
||||
|
|||||
Рис. 4.35 |
|
|
|
|
|
Примеры звена.
1. Двигатель постоянного тока (рис. 4.36), если допустить, что TЯ=0, TМ=0 и в качестве выходной величины рассматривать угол поворота якоря, а в качестве входной – напряжение якорной цепи.
Uв |
Uя=x1 |
G=x1 |
|
||
|
α=x2 |
H=х2 |
|
|
|
Рис. 4.36 |
|
Рис. 4.37 |
2.Гидравлический резервуар (рис.4.37). Входным воздействием является расход воды G, поступающий в резервуар, а выходной величиной уровень воды в резервуаре H. Входная и выходная величины связаны зависимостью S dH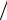 dt = G , где S – площадь поперечного сечения
dt = G , где S – площадь поперечного сечения
резервуара.
3. Модель интегрирующего звена
71
С
R
|
|
|
|
|
U1=x1 |
|
U2=x2 |
||
|
||||
Рис. 4.38
4.4.2. Интегрирующее звено с замедлением
Дифференциальное уравнение звена
T ddt2 x22 +dxdt2 =kx1 .
Передаточная функция звена
W ( p)= p(Tpk +1) ,
то есть соответствует идеальному интегрирующему звену и апериодическому звену первого порядка, соединенным последовательно.
|
|
|
|
|
|
|
− |
t |
|
|
|
|
|
x =1(t); |
h(t)= x |
|
T |
)]×1(t) |
|
||||||||
2 |
(t)=k[t −T (1−e |
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
x2 |
|
|
|
kt |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
h(t) |
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.39 |
|
|
|
T |
Рис. 4.40 |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
V |
|||||
Частотная передаточная функция |
|
|
|
|
|
||||||||
W ( jω) = |
|
k |
|
|
|
|
|
|
|
|
|
ω=∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
jω(Tjω+1) |
|
|
|
|
|
U |
||||||
ω→0
Рис. 4.41
72
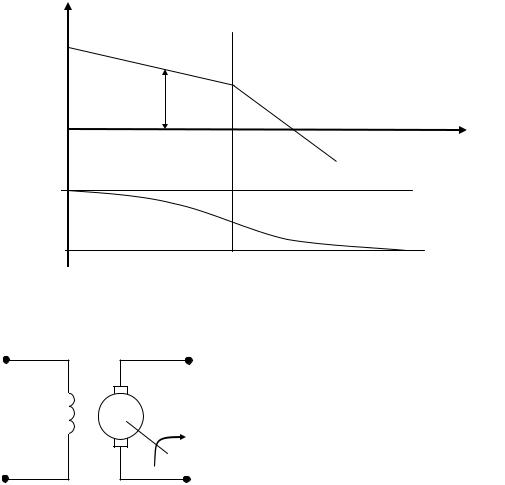
Логарифмические частотные характеристики
ϕ(ω) |
L(ω) |
1/T |
|
|
|
|
-20дБ/дек |
|
|
-20lgk |
-40дБ/дек |
ω,с-1
-90°
ϕ(ω)
-180°
Рис. 4.42
Пример: двигатель постоянного тока при Tя=0; Tm≠0
U1=x1
0
ϕ=x2
Рис. 4.43
4.4.3. Пропорционально-интегральное звено
Описывается уравнением
dxdt2 =kx1 +k1 dxdt1 .
Передаточная функция имеет вид
W ( p)= |
k |
+k |
= |
k(1+Tp) |
, где T = |
k1 |
- постоянная времени. |
|
p |
p |
|||||||
|
1 |
|
|
k |
|
Переходная функция
x2(t) =h(t) =(kt +k1)×1(t)
