Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Казанский национальный исследовательский технический университет им. А. Н. Туполева
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

u_lectures

.pdf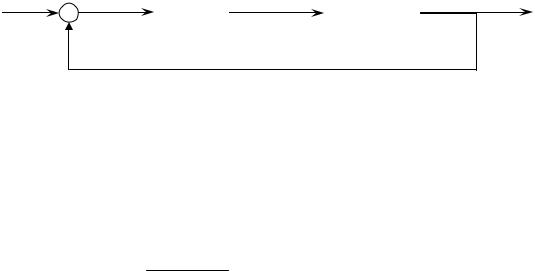
Скачиваний:
52
Добавлен:
22.03.2016
Размер:
2.16 Mб
Скачать
☆
Wp ( z )

193

Допустим, что a0 =1. Это всегда можно сделать, если поделить на a0 . Последнее выражение представляет собой разностное уравнение,

которое связывает две решетчатые последовательности u0 [nT ]и e0 [nT ]. Из него можно получить алгоритм работы ЦВМ при a0 =1.

u0 ( nT ) = b0e0 ( nT ) + b1e0 [(n −1)T ]+K+ bk e0 [(n − k )T ]− −{a1u0 [(n −1)T ]+ a2u0 [(n − 2)T ]+K+ ak u0 [(n − k )T ]}.

В соответствии с этим выражением должно формироваться значение выходного сигнала ЦВМ. При этом используются текущее значение входного сигнала e0 (nT ), а также предыдущие значения входного и

выходного сигналов, хранящиеся в памяти ЦВМ.

Таким образом, ЦВМ соответствует фильтру с передаточной функцией

D( z ).

Если в установившемся режиме, то есть при z = 1, D( z ) равно конечному числу, то фильтр соответствует статическому звену.

Если D( z )

содержит сомножитель (z – 1) в знаменателе, то ЦВМ

выполняет интегрирующие операции.

 

 

 

 

23.6. Передаточные функции цифровой САУ

Структурная схема цифровой САУ

с учетом рассмотренного ранее

имеет вид

 

 

 

 

 

 

X(n)

 

 

U(n)

 

 

y(n)

 

D(z)

 

WH(z)

−

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 23.8

Тогда передаточная функция разомкнутой системы:

Wp(z) = D(z) WH(z).

Передаточная функция замкнутой системы:

W( z ) = 1 +Wp ( z ) .

194

23.7. Приближенное определение дискретной передаточной функции по передаточной функции непрерывной части

(подстановочный метод)

Проектирование цифровых САУ может быть выполнено на основе двух подходов:

1)Первый подход основан на синтезе системы, рассматриваемой как непрерывная, в области комплексной переменной «р». Синтезируется аналоговый регулятор. Затем производится его дискретная аппроксимация и определяется алгоритм работы цифровой части системы.

2)При втором подходе описание непрерывного объекта заменяется дискретной аппроксимацией, в результате чего вся система оказывается описанной в области комплексной переменной «z», а алгоритм работы цифровой части определяется в результате синтеза дискретной системы.

Для обоих подходов необходимо определить передаточную функцию дискретной системы, которая определяется двумя способами:

1)Первый способ основан на использовании таблиц z – преобразования (рассмотрен ранее и является точным методом).

2)Второй широко используемый метод перехода от непрерывного математического описания к дискретному является подстановочный (один из вариантов его рассмотрен при реализации алгоритма ПИД – регулятора на ЦВМ). Рассмотрим его более подробно.

Подстановочный метод получения дискретной передаточной функции.

Он основан на дискретной аппроксимации аналоговых интеграторов и

подстановки вместо комплексной переменной

1

следующих выражений.

p

 

 

 

 

 

 

 

 

 

 

 

1

=T

1

 

;

 

 

 

(23.1)

 

p

z −1

 

 

 

 

 

 

 

 

 

 

1

=T

 

z

 

;

 

 

 

(23.2)

 

p

z −1

 

 

 

 

 

 

 

 

 

 

1

= T

 

z +1

 

;

 

(23.3)

 

p

z −1

 

 

2

 

 

 

 

Вместо

выражений (23.1) – (23.3) можно

подставить аналогичные им.

 

 

 

 

195

p =

z −1

;

 

(23.4)

T

 

 

 

 

 

p =

z −1

;

 

(23.5)

T z

 

 

 

 

 

p =

2(z −1)

;

(23.6)

T (z +1)

 

 

 

Пример.

Пусть передаточная функция непрерывной системы Wp ( p)

= T1 pk+1 .

Ей соответствует точная передаточная функция, определенная по таблицам z–преобразования

 

 

−T

 

 

 

k 1

−e

T1

 

 

 

 

 

 

 

 

Wp (z) =

 

 

 

 

;

(23.7)

 

−

T

 

 

 

T1

 

 

 

 

z −e

 

 

 

Эта передаточная функция определена ранее в одном из примеров при условии, что импульсное звено имеет прямоугольные импульсы.

Найдем дискретную передаточную функцию с помощью метода подстановки. Подставим (23.4) в Wp(p)

 

 

k

 

 

 

 

k

 

k

T

 

 

k

T

 

 

Wp (z) =

 

 

=

 

 

=

 

T

 

=

 

T

 

(23.8)

 

 

 

 

 

 

 

 

1

 

 

1

 

 

z −1

 

 

T1

 

 

 

T

 

T

 

 

T

+1

 

(z −1) +1 z −1+

 

 

 

 

 

T

T1

 

 

 

 

 

1 T

 

 

 

 

 

 

 

 

z − 1− T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

Выражение (23.8) является приближенным и совпадает с (23.7) при

малых значениях T :

T1

−TT

 

T

 

 

 

 

 

 

 

 

 

 

(23.9)

e 1 ≈1− T

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

Подставим (23.9) в (23.7) и получим

 

 

 

k

 

 

− T

 

 

k

T

 

 

 

 

1− 1

 

 

 

T

 

 

 

 

 

 

 

 

 

 

T1

 

 

 

 

 

Wp (z) =

 

 

 

 

 

 

 

 

=

 

1

 

 

(23.10)

 

 

 

 

−

T

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

z − 1

 

 

 

z − 1−

 

 

 

 

 

 

 

 

T1

 

 

 

 

T1

 

Выражение (23.10) совпадает с (23.8).

Пример 2.

196

Если вместо р подставить p = Tz −z1 , то получим

Wp (z) =

 

 

 

 

k

 

 

 

=

 

k z

 

=

 

 

k z

 

 

 

T1

(z −

1)

+1

T1

(z −1)

+ z

 

 

T

 

T

 

 

 

 

 

 

 

 

Tz

 

 

 

T

 

1

+

1

z −

1

 

 

 

 

 

 

 

 

 

 

 

T

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k 1

+

 

1

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z −

 

 

T1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T +T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

−1

z

 

 

k 1+

1

 

 

 

=

 

 

 

T

 

 

 

=

z −

T

 

 

 

T

−1

 

 

 

 

 

1

1+

1

 

 

T

T

 

 

 

 

 

 

 

 

(23.11)

Передаточная функция (23.11) отличается от(23.8).

Метод достаточно прост. К недостаткам относится то, что для сложных передаточных функций выражения громоздки и изменение одного из параметров передаточной функции Wp(p) требует пересчета всех коэффициентов Wp(z).

Структурный метод аппроксимации непрерывных передаточных функций.

Основан на подстановке выражений (23.1)–(23.3) или (23.4)–(23.6) в детализированную структурную схему.

Пример:

Пусть передаточная функция непрерывной системы имеет вид

Wp ( p) =

k

 

хвх

 

хвых

 

T p +1

 

 

 

 

 

 

1

 

 

Wp(p)

 

 

 

 

 

 

 

 

 

 

 

 

Представим ее в детализированной форме

хвх

к

 

1

 

хвых

 

 

 

T1 p

 

 

 

 

 

 

 

 

 

 

−

 

 

 

 

 

 

 

 

 

 

Заменим 1p = zT−1 и получим

хвх(z)

к

 

 

 

T

 

хвых(z)

 

 

 

T1

(z −1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

197

−

Найдем передаточную функцию

Wp (z) = xxвых((zz)) =

вх

k

 

 

T

T (z −1)

 

 

 

1

 

 

1+

 

T

T

(z −1)

 

 

 

 

1

 

 

 

k

T

 

k

T

 

 

 

=

 

T

=

 

T

 

 

(23.12)

 

1

 

1

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

z −1+ T1

 

z − 1− TT

 

 

 

 

 

 

 

 

1

 

Выражение (23.12) совпадает с (23.8).

24. РЕАЛИЗАЦИЯ НА МИКРОЭВМ ЦИФРОВЫХ АЛГОРИТМОВ УПРАВЛЕНИЯ

Реализация алгоритмов управления на микроЭВМ часто требует выполнения операций дифференцирования и интегрирования над некоторыми цифровыми последовательностями.

24.1. Дифференцирование цифровых последовательностей

Рассматривается задача, когда непрерывная функция времени f(t) дискретизируется по времени и уровню и представляется в виде цифровой последовательности f(nT) c периодом Т.

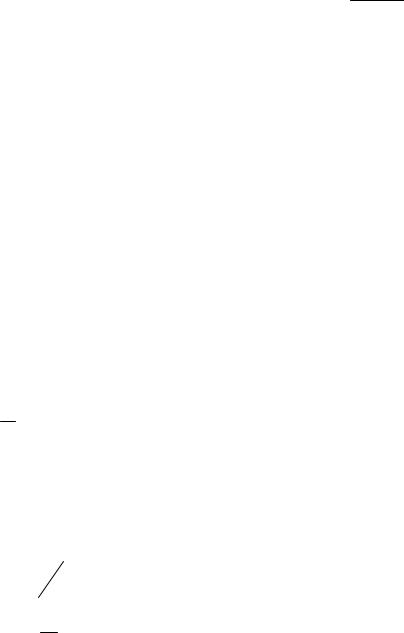
198

Требуется найти наилучшее приближение производной непрерывной

•

функции времени df(t)/dt к её производной в цифровой форме f (nT ) . В

непрерывных системах оператором дифференцирования является p = d/dt.

•

Для вычисления f (nT ) необходимо найти алгоритмы дифференцирования, реализуемые на ЦВМ.

Известно, что z = epT , откуда найдем p = lnTz . Последнее выражение можно разложить в ряд тремя способами:

p =

1

(z −1)− 1 (z −1)2

+ 1 (z −1)3 −K

;

(24.1)

 

 

T

 

 

 

 

 

2

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p =

2

z −1

 

1

z

−1 3

 

1

z −1

5

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

+

 

 

 

 

 

 

 

+K

;

(24.2)

T

 

 

 

3

 

 

5

 

 

 

 

 

z +1

 

z

+1

 

z +1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

−1

 

 

1

 

 

−1

 

2

 

 

1

 

 

 

−1

 

3

 

 

 

p =

 

(1

− z

 

)

+

 

(1− z

 

)

 

+

 

(1

− z

 

)

 

+K

(24.3)

T

 

2

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Оператор z1 соответствует упреждению на 1 такт, z2 соответствует упреждению на 2 такта и так далее, z -1 – соответствует задержке на один такт.

Поэтому выражение (24.1) можно использовать, когда известны будущие значения дифференцируемой функции. Выражение (24.2) не может быть использовано для целей дифференцирования, так как будет получена неустойчивая программа обработки на ЦВМ. Это следует из того, что в знаменателе всех слагаемых есть корень z1 = –1, соответствующий границе колебательной устойчивости.

Выражение (24.3) может быть использовано для дифференцирования, так как для его реализации необходимо знать текущее и прошлое значения обрабатываемой функции.

Обычно используется первый член выражения (24.3), тогда получим:

f

(z) =

T1 (1− z−1 ) f (z)

•

 

 

 

или перейдя к оригиналам

f (n) = 1

[ f (n) − f (n −1)].

•

 

 

T

 

Таким образом, передаточная функция операции численного дифференцирования будет равна

•

D(z) = ff ((zz)) = T1 (1− z−1 ).

199

Или в структурной форме

f (z)

 

 

•

 

D(z)

 

f (z)

 

 

 

24.2. Цифровые интеграторы

 

Рис. 24.1

 

 

Рассматривается задача интегрирования непрерывной функции f(t), представленной в виде цифровой последовательности.

Необходимо найти алгоритм цифрового интегрирования, обеспечивающий наилучшее приближение выходной величины к цифровой последовательности, образованной дискретизацией интеграла от f(t) по времени.

Так как операция интегрирования обратна операции дифференцирования, то в качестве оператора рассматривается величина 1/p, где p = d /dt. Эту величину можно получить из формул (24.1)÷(24.3) путем их обращения, рассматривая только первое слагаемое.

Тогда получим:

1

≈

T

 

 

=

T z−1

 

 

p

z −1

1

− z−1

 

 

 

 

 

 

 

1

≈

T

 

z +1

=

T

 

1+ z−1

 

 

 

 

 

 

 

 

 

 

− z−1

p

2

z

−1

2

1

 

 

 

 

1

≈

 

T

 

 

 

 

 

 

 

 

 

p

1− z−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(24.4)

(24.5)

(24.6)

Формула (24.4) соответствует численному интегрированию методом прямоугольников и ее можно также получить другим способом.

f(p)

 

F(z)

 

WФ(p)

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

x(p)

X(z)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 24.2

 

 

 

 

 

 

 

 

 

T z−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

X (z)

 

z −1

 

 

1

 

 

 

z −1

 

T z

 

 

 

 

 

T

 

 

 

 

 

=

 

 

Ζ

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

=

 

−1 .

F(z)

z

 

2

 

z

(z −1)

2

z −1

1− z

 

 

p

 

 

 

 

 

 

 

 

 

 

 

Разностное уравнение получим, перейдя от изображений к оригиналам:

X(z) (1− z−1 )= F(z) T z−1

x[n]= x(n −1) +T. f (n −1)

200

На рис. 24.3 приведена геометрическая интерпретация разностного уравнения.

f(t)

с упреждением

 

 

 

аппроксимация f(t)

 

 

 

x(n)

Т

2Т

3Т

4Т

 

Рис. 24.3

 

Формула (24.6) соответствует численному интегрированию методом прямоугольников с упреждением и имеет разностное уравнение

x(n) = x(n −1) +Tf (n) .

Этот способ дает скачок при t = 0, хотя в дальнейшем переходная функция близка к истинной. Вид аппроксимирующей функции изображен на рис. 24.3 пунктиром.

Формула (24.5) соответствует интегрированию методом трапеций. Разностное уравнение имеет вид:

X(z) (1− z−1 )= T2 (1+ z−1 ) F(z), x(n) = x(n −1) + T2 [ f (n) + f (n −1)].

24.3.Обобщенная формула численного интегрирования.

Компенсация ошибок

Численное интегрирование выполняется с ошибками, источники которых многочисленны. Наиболее существенны для замкнутых систем фазовые искажения, которые уменьшают устойчивость САУ. Для их компенсации вводят корректирующее звено с передаточной функцией

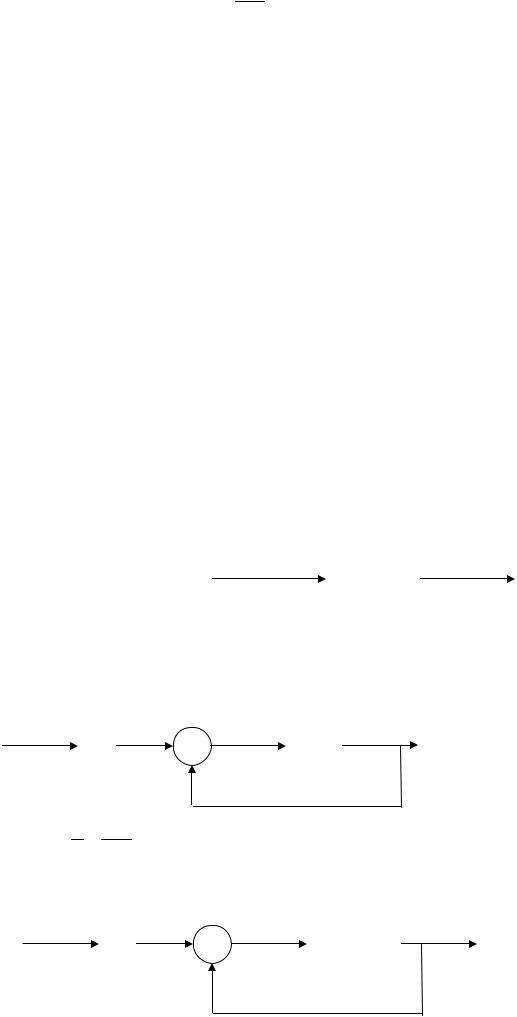
Wk ( p) = eγ pT ≈1+γ pT , где γ - коэффициент коррекции по фазе. Непрерывный процесс интегрирования представлен на рис. 24.4.

f(p) 1 X(p)

p

Рис. 24.4

201

Структурная схема дискретного процесса интегрирования (рис. 24.5).

f(p)

F(z)

~f(p)

1+γpT

~X(p)

X(z)

 

z −1

 

1

 

 

 

 

1

 

 

 

 

eγpT

 

 

z

 

p

 

 

 

 

p

 

 

 

 

Рис. 24.5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Передаточная функция

X (z)

 

z −1

 

 

 

 

 

z −1

 

 

1

=

 

Ζ 1+γ pT

 

=

Ζ

 

F(z)

z

 

 

 

 

p2

 

 

 

z

 

p2

γz +(1−γ )

γ + (1−γ ) z

−1

 

 

= T

 

z −1

 

= T

1− z

−1

 

 

 

 

 

 

 

 

 

 

 

Откуда получим:

такой аппроксимации

 

γT

 

 

z −1

 

 

Tz

 

γTz

 

 

 

+

 

=

 

 

+

 

=

p

z

(z −1)2

z −1

 

 

 

 

 

 

 

X (z) = X (z) z−1 +T γ F(z) + (1−γ )F(z)z−1 .

Тогда разностное уравнение:

x(n) = x(n −1) +T [γ f (n) + (1−γ ) f (n −1)].

Изменение значения γ приводит к формулам численного интегрирования с разными фазовыми характеристиками, в том числе и к классическим формулам интегрирования.

При различных γ получим:

γ= 1 – метод прямоугольников с упреждением;

γ= 0,5 – метод трапеций;

γ= 0 – метод Эйлера (метод прямоугольников).

24.4.Дискретные регуляторы

ВСАУ широко применяются регуляторы, имеющие следующие составляющие в законе регулирования: пропорциональную, интегральную, дифференциальную.

Рассмотрим переход от аналогового регулятора к цифровому. Передаточная функция аналогового ПИД-регулятора имеет вид

W ( p) = k

1+

1

+T p

 

=

U ( p) .

(24.7)

T p

 

 

 

D

 

X ( p)

 

 

 

I

 

 

 

 

 

202

Используя метод интегрирования способом прямоугольников, то есть выражение (24.4) и (24.3), получим дискретную передаточную функцию

 

 

 

U (z)

 

 

 

 

 

 

 

 

 

T

 

 

 

z−1

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W (z) =

X (z)

= k

1+

 

 

 

 

 

+

 

 

D

 

(1− z

 

 

)

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

1− z−1

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−1

 

 

T

 

 

 

 

−1

 

 

 

T

 

(1− z

−1

)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

(1− z

 

)

+

 

 

z

 

 

 

 

+

 

D

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1− z−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Откуда найдем:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U (z) (1− z

−1

)= k

 

 

 

−1

)

+

 

T

z

−1

+

 

T

 

 

(1− z

−1

)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(1− z

 

 

 

T

 

 

 

 

T

 

 

 

 

X (z);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

D

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U (z) =U (z) z

−1

+ k

 

T

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

T

 

 

z

−1

 

 

 

T

 

z

−2

 

X (z)

 

 

 

 

 

 

 

1+

 

D

+

 

−1+

 

 

 

 

 

− 2 D

 

 

 

+

 

D

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

TI

 

 

 

T

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отсюда получим разностное уравнение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

u(n) = u(n −1) + k

 

1

 

+

 

 

D

x(n) +

−1+

 

 

 

 

 

−

2

 

 

D

 

x(n −1) +

 

D

x(n − 2)

 

 

 

 

 

TI

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

или

сокращенно

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u(n) = u(n −1) + q0 x(n) + q1x(n −1) + q2 x(n − 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(24.8)

 

 

где q

= k 1+

TD

 

,

 

q = k

 

−1+

T

− 2

TD

 

,

 

q = k

TD

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

T

 

 

 

1

 

 

 

 

 

 

 

 

 

 

T1

 

 

 

 

 

T

 

 

 

 

 

 

2

 

 

 

 

T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выражение (24.8) является основой алгоритма, реализуемого на ЭВМ. Для сокращения обозначено u(n) = u(nT). Таким образом, для вычисления u(nT) на данном шаге квантования необходимо иметь u[(n-1)T] и

значения входного сигнала в моменты времени: nT; (n-1)T; (n-2)T. Коэффициенты qi зависят от параметров аналогового регулятора, но

для конкретной реализации регулятора будут постоянны.

Частный случай. ПИ – регулятор.

Если в последних выражениях положить TD = 0, то получим выражение, соответствующее ПИ – регулятору.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности