
u_lectures
.pdf
33
Рассмотрим примеры: |
|
|
|
|
|
|||||||||||
1) Пусть W(jω)=K1, тогда |
|
|
|
|
|
|||||||||||
|
A(ω)=К1 и |
L(ω) =20lg A(ω) =20lgK1 |
||||||||||||||
ϕ(ω) |
|
L(ω) |
1 |
|
|
|
|
4 |
20дБ/дек |
|||||||
60° |
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
20lgK1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
40° |
20 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
20° |
|
10 |
|
|
|
|
|
|
|
20lgK2 |
20lgK3 |
|
|||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω,1/сек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20° |
|
|
|
1 |
|
10 |
|
|
|
|
|
100 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
-20дБ/дек |
|
|
|
|
||||
-40° |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-60° |
|
|
|
|
|
-40дБ/дек |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Рис. 3.9 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
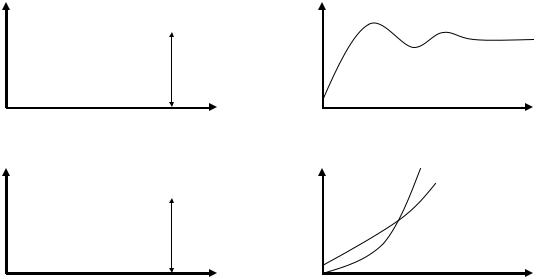
2) W ( jω) = Kω2 ; тогда j
A(ω) = K2 |
; |
L(ω) =20lg K2 −20lgω |
ω |
|
|
если обозначить lgω = x , то L(ω) =20lgK2 −20x . Пусть ω=1, тогда L(ω) =20lgK2 .
Определим наклон прямой, для этого вычислим L(ω) при ω1и 10ω1
L(10ω1)−L(ω1) =20lgK2 −20lg10ω1−(20lgK2 −20lgω1) =−20дБ , то есть за
одну декаду L(ω) уменьшится на 20дБ и наклон прямой составляет –20 дБ/дек.
3) W ( jω) = |
K3 |
|
( jω)2 |
||
|
A(ω) =ωK23
L(ω) =20lg K3 −20lgω2 =20lgK3 −40lgω
L(ω) также имеет вид прямой с наклоном –40дБ/дек.
4)W ( jω) =K4 jω
A(ω) = K4 ω
L(ω) =20lgK4 +20lgω
Это уравнение прямой с наклоном +20дБ/дек.
34
3.4. Понятие об устойчивых минимально-фазовых звеньях
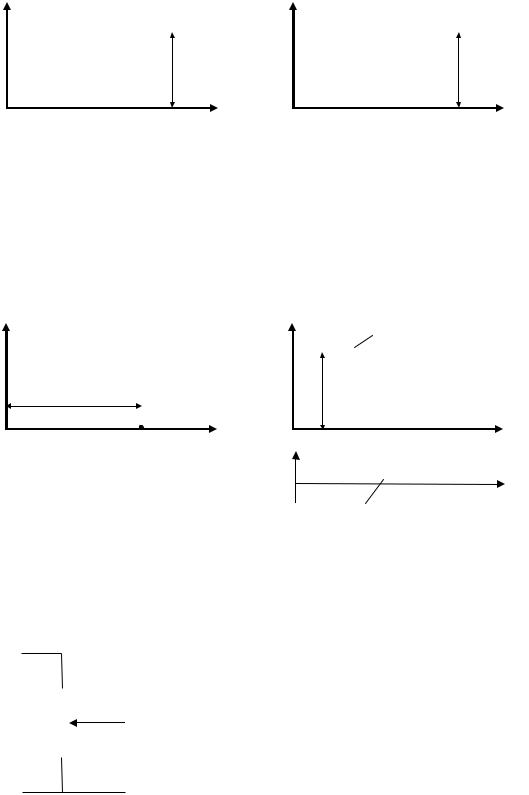
Звено называется устойчивым, если при ступенчатом воздействии на входе звена, его выходная величина устанавливается на некотором определенном значении.
x1 |
|
|
|
|
|
|
|
|
|
x2 |
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Устойчивое |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 3.10 |
|
|
|
|
Рис. 3.11 |
|||||||
x1 |
|
|
|
|
|
|
|
|
|
x2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неустойчивое |
|||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
|
|
Рис. 3.12 |
|
|
|
|
|
Рис. 3.13 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Устойчивость можно определить по передаточной функции звена |
||||||||||||||||
|
|
B( p) |
|
b pm +b pm−1 |
+K+b |
|||||||||||
W ( p) = |
= |
|
0 |
1 |
|
m |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
A( p) |
|
a0 pn +a1pn−1 +K+an |
||||||||||||
Передаточную функцию звена можно представить в виде: |
||||||||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
П ( p − qj |
) |
|
|
|
|
|
|
|
|
|||
W ( p) = |
0 |
j |
=1 |
|
|
, |
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
( p − r ) |
|
|
|
|
|
|
||||||
|
|
|
П |
|
|
|
|
|
|
|||||||
|
|
|
|
0 i = |
1 |
i |
|
|
|
|
|
|
|
|
|
|
где qj – нули W(p), которые являются корнями уравнения B(p) = 0,
ri – полюсы W(p) или корни уравнения A(p) = 0,
П – знак произведения.
Устойчивость звена определяется корнями полиномов. Для устойчивых звеньев полюсы имеют отрицательные вещественные части, при
35
этом свободная составляющая решения дифференциального уравнения содержит слагаемые типа Ci eri t , которые стремятся к нулю.
Минимально-фазовые звенья имеют все нули и полюсы W(p) с отрицательными вещественными частями. Название звеньев обусловлено тем, что этим звеньям присущи меньшие по абсолютной величине фазовые сдвиги по сравнению со звеньями, где это условие не выполняется.
Для этих звеньев справедливы зависимости:
|
|
|
|
∞ |
ω |
|
|
1 |
∞ U(ω ) |
|
||
U (ω) = − |
1 |
|
∫ |
V ( ) du ; |
V(ω ) = |
|
|
∫ |
du ; |
|||
π |
||||||||||||
|
π |
−∞ u −ω |
|
|
−∞ u −ω |
|
||||||
ϕ(ω) = |
1 |
|
∞ ln A(u) |
du . |
|
|
|
|
|
|||
|
|
|
∫ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
8,7π −∞ u −ω |
|
|
|
|
|
|
|||||
где u – переменная интегрирования. Эти выражения вытекают из преобразований Гильберта и имеют важное значение, так как дают однозначное соответствие между АЧХ и ФЧХ, а также АЧХ и W(jω).
4. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
Любую САУ можно разделить на ряд элементов, которые описываются определенными дифференциальными уравнениями. Причем одним классом дифференциальных уравнений могут описываться элементы различной физической природы (электрические, механические, тепловые и т.д.). Этот факт позволяет все многообразие элементов систем изучать на основе ограниченного числа типовых динамических звеньев.
Поэтому класификация звеньев осуществляется именно по типу дифференциального уравнения или по виду передаточной функции.
Для каждого звена будем рассматривать следующие характеристики:
1.дифференциальное уравнение,
2.передаточная функция – W(p);
3.переходная функция – h(t);
4.частотные характеристики: W(jω), L(ω), ϕ(ω);
5.примеры.
4.1. Безынерционное или пропорциональное звено
Описывается в статике и динамике уравнением
x2 = Kx1,
где K - коэффициент усиления или передачи звена.
Передаточная функция имеет вид
|
|
|
36 |
|
|
|
W(p) = K. |
|
|
|
|
Переходная функция звена |
h(t) = K ×1(t) = K . |
||||
x1 |
x2 |
|
h(t) |
||
|
|
|
|
|
|
1 |
|
|
K |
||
|
|
t |
|
|
t |
|
|
|
|
|
|
|
Рис. 4.1 |
|
|
Рис. 4.2 |
|
|
|
|
|
|
|
Частотнвя передаточная функция имеет вид
W(jω) = K.
Характеристики изображены на рис. 4.3 – 4.5.
V(ω) |
|
L(ω) |
|
L(ω)=20lgK |
|
|
|
|
|
|
|
K |
|
U(ω) |
|
20lgK |
|
|
|||||
|
|
|
|
|
|
Рис. 4.3 АФХ |
|
ϕ(ω) |
|
Рис. 4.4. ЛАЧХ |
|
|
|
||||
|
|
|
|
|
|
|
0° |
|
|
|
|
|
|
ϕ(ω)=0° |
|||
|
|
|
|
||
|
|
|
|
Рис. 4.5. ЛФЧХ |
|
Примеры звеньев.
1) Делитель напряжения.
Uвх |
|
|
R1 |
UВЫХ = K UВХ, |
|
R2 Uвых K= R2/(R1+R2). |
|||
|
|
|||
|
|
|||
Рис
.
2) Электронный усилитель
ω
ω
|
|
|
|
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электронный |
|
|
|
|
|
|
|
|
Uвых = K Uвх |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Uвх |
|
|
|
|
Uвых |
|
|
|
|
|
|
|||||||
|
|
усилитель |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
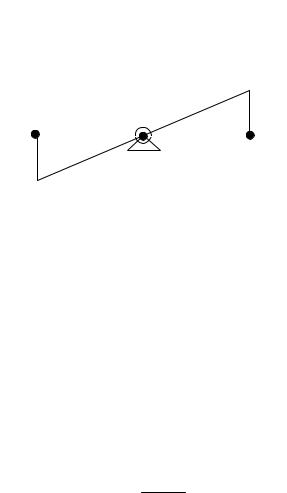
3) Механический рычаг. |
|
|
|
|
|
|
Если пренебречь массой рычага, то |
||||||||||||
|
|
|
|
Рис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
|
|
x2 |
|
l2 |
x |
= Kx , где |
|
l2 |
|
||||
|
|
|
|
|
|
|
|
x |
= |
K = |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
l1 |
1 |
1 |
|
l1 |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x1 |
|
|
|
|
l2 |
|
|
|||||||||||
|
|
|
Рис. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2. Апериодическое звено первого порядка
Описывается уравнением
T |
dx2 |
+ x |
2 |
= kx |
; |
|
|||||
|
dt |
1 |
|
||
|
|
|
|
||
где: k – коэффициент усиления, T – постоянная времени. Передаточная функция
W ( p) =Tpk+1 .
Найдем переходную функцию звена, решив дифференциальное уравнение. Характеристическое уравнение имеет вид
Tr +1=0 ;
Откуда единственный корень |
r =− |
1 |
. |
|
|||
|
T |
||
Тогда общее решение дифференциального уравнения
|
|
|
|
|
− |
t |
|
|
|
|
|
|
= Cert |
|
|
||
|
|
|
|
= Ce T . |
|
|||
|
x |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
Если x (t) =1(t) , то частное решение |
x =k . |
|||||||
|
|
1 |
|
|
|
|
2 |
|
Тогда
* |
−t |
||
x2 = |
|
+ x2 =Ce T +k ; |
|
x2 |
|||
Подставив начальные условия: t = 0, x2 = 0, получим x2(0) = С + k = 0, откуда C = – k.

38
Окончательное выражение для переходной функции (рис. 4.10) примет
вид
|
− |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 = h(t) = k(1−e T ) . |
|
|
|
|
|
|
|
|||
x1 |
|
x2 |
T |
|
|
|
|
|||
|
|
|
||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
h(t) |
K |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
Ри |
|
|
|
|
|
Рис. |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
4 10 |
Частотная передаточная функция
W ( jω) = Tjωk +1
Ее можно представить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W ( jω) = |
k |
|
× |
(−Tjω +1) |
= |
|
|
k |
|
|
|
− j |
|
kTω |
|
; |
||||
Tjω +1 |
(−Tjω +1) |
|
2 2 |
+1 |
|
2 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
T |
|
ω |
|
T |
ω |
+1 |
||||||
U (ω) = |
|
|
k |
|
|
; |
V (ω) = − |
kTω |
|
; |
|
|
|
|
||||||
|
2 2 |
|
2 2 |
|
|
|
|
|
|
|
||||||||||
T |
|
ω |
+1 |
|
|
|
|
T ω |
+1 |
|
|
|
|
|||||||
Годограф изображен на рис. 4.11.
|
V |
|
|
|
|
|
|
|
|
|
U(ω1) |
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ω=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ω→∞ |
|
|
|
|
|
|
ϕ(ω1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
V(ω1) |
|
|
|
|
A(ω1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ω2 |
|
|
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Рис. 4.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A(ω) = U |
2 |
(ω) +V |
2 |
(ω) |
= ( |
|
k |
|
) |
2 |
+( |
|
kTω |
|
) |
2 |
= |
k 2(T 2ω2 +1) |
= |
||||||||
|
|
|
|
2 2 |
|
|
|
2 2 |
|
|
2 2 |
+1) |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
ω |
+1 |
|
T |
ω |
+1 |
|
|
(T ω |
|
|
|||||
= |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2ω2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
39
A(ω) = |
k |
|
; |
|
|
|
T × ω2 + |
1 |
|
|
|
||
|
|
|
|
|
||
|
T 2 |
|
|
|
|
|
L(ω) =20lgk −20lgT |
|
ω2 + |
1 |
; |
||
|
|
|||||
|
|
|
|
T 2 |
|
|
ϕ(ω) =arctg UV ((ωω)) =arctg(−Tω) =−arctgTω;
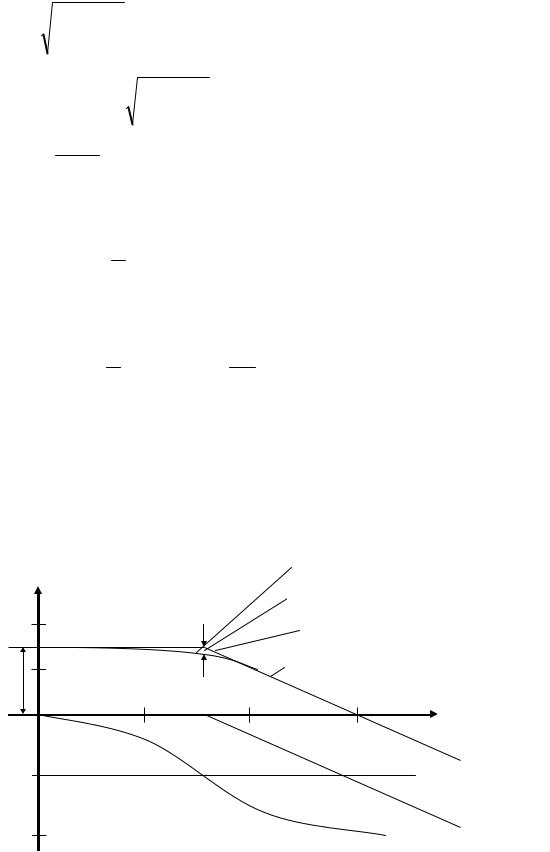
Построим ЛАЧХ (рис. 4.12)
1)Пусть ω <T1 , тогда пренебрегаем ω и считаем ω2 ≈ 0
L(ω) =20lgk −20lg1=20lgk
2)Пусть ω > T1 , тогда ω2 >> 12T
L(ω) =20lgk −20lgTω = L1(ω) +L2(ω)
Определим наклон L2(ω) на декаду
−20lgT 10ω −(−20lgT ω) =−20lgTω −20lg10+20lgTω =−20дБ/дек
L(ω) |
|
|
|
|
Приближенная (асимптотическая) |
||
|
|
|
Погрешность 3 дБ |
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
40 |
|
|
Точная |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
20lgk |
20 |
|
-20дБ/дек |
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω,с-1 |
|
ϕ(ω) |
1 |
10 |
|
100 |
|
||
|
|
|
|
|
|
|
|
-45° |
|
|
|
|
|
|
|
|
|
|
|
ϕ(ω) |
L2(ω |
||
-90° |
|
|
|
|
|
|
|
|
|
|
|
Ри |
|
|
|
40
Примеры звена.
1. RC–цепь, изображенная на рис. 4.13.
Приведенная RC–цепь описывается уравнением
RC |
du2 |
+ u2 = u1 , |
|
|||
dt |
|
|||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
где T=RC – постоянная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
времени звена. |
u1 |
|
|
|
|
C |
|
|
|
u2 |
||||
Рис. 4.13
Передаточная функция может быть найдена также через комплексные сопротивления ветвей
z ( p ) = R; z |
2 |
( p ) = |
1 |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
Cp |
|
1Cp |
|
|
|
|
|||
W ( p) = |
U2( p) |
= |
|
I ( p) z2( p) |
|
== |
= |
1 |
|
. |
||||
U1( p) |
I ( p)[z2( p) + z1( p)] |
|
|
|
||||||||||
|
|
|
R + 1Cp |
RCp +1 |
|
|||||||||
2. Генератор постоянного тока, приведенный на рис. 4.14.
Свойства генератора описываются передаточной функцией
Uв=x1 Г
Рис. 4.14
W( p ) = |
EГ ( p ) |
|
= |
|
KГ |
|
, |
||
|
T p + 1 |
||||||||
|
U |
В |
( p ) |
|
|
||||
Eг=x2 |
|
|
|
|
|
В |
|
||
|
|
|
|
|
|
|
|
|
|
где UВ – напряжение обмотки
возбуждения; ЕГ – э.д.с. генератора; TВ – электромагнитная постоянная обмотки
возбуждения; КГ – коэффициент передачи генератора.
4.3. Звено второго порядка

41
Его динамические свойства описываются дифференциальным уравнением второго порядка
T22 d 2 x2 +T1 dx2 + x2 = kx1 . dt2 dt
Звену соответствует передаточная функция:
W ( p) = |
|
k |
|
|
|
. |
|
T 2 p2 |
+T p +1 |
||
2 |
1 |
|
|
Характеристическое уравнение звена и его корни имеют вид
T 2 r2 |
+T r + 1 = 0; |
r = |
−T ± |
T 2 |
− 4T 2 |
|
1 |
1 |
2 . |
||||
2 |
1 |
1,2 |
|
2T |
2 |
|
|
|
|
|
2 |
|
|
Возможны два случая:
1.T12 − 4T22 < 0 – корни комплексные, а звено называется колебательным;
2.T12 − 4T22 ≥ 0 – корни действительные отрицательные, а звено является апериодическим второго порядка.
4.3.1. Колебательное звено
Передаточную функцию звена в этом случае принято записывать в следующем виде
k |
|
|
W ( p) = T 2 p2 + 2ξTp +1 , |
||
где T = T2 , 2ξT = T1 . |
|
|
Откуда определим ξ = |
T1 |
< 1 - показатель колебательности. |
|
2T |
|
Корни характеристического уравнения будут равны
r |
= |
− 2ξT ± |
4ξ2T 2 − 4T |
2 |
|
|
=α ± jβ, |
||
1,2 |
|
|
2T 2 |
|
|
|
|
|
42
где α = − |
ξ |
– вещественная часть корней; |
β = |
1 |
1−ξ 2 |
– мнимая часть |
|
T |
T |
||||||
|
|
|
|
|
корней.
Если на вход поступает воздействие x1=1(t), то найдем переходной процесс. x*2=k;
x2 =[k+eαt (C1cos βt+C2 sin βt)]1(t)
Пусть при t=0; (x2)0=0 и (x΄2`)0=0
(x2)0 =k +C1 =0 |
C1 =−k |
|
|
|
(x2′)0 =αC1 +βC2 =0 |
C2 |
=−αC1 |
= |
αk |
|
|
β |
|
β |
x2 = h(t) = K[1 − eαt (cos βt − αβ sin βt)] 1(t).
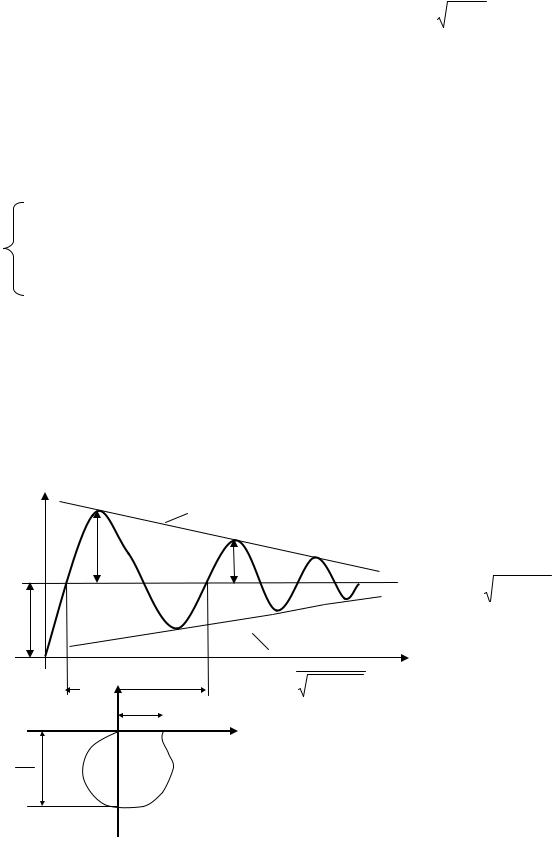
Переходный процесс изображен на рис. 4.15. На основе полученной переходной функции можно определить параметры передаточной функции.
x2
K
k
2ξ
|
|
|
|
|
|
|
Из рис. 4.15 следует: |
||||||||
|
|
|
k(1+eαt) |
|
|
β = |
2π |
; α = |
1 |
ln |
A2 |
; |
|||
|
h(t) |
|
|
|
|
τ |
τ |
A |
|||||||
|
|
A2 |
|
|
|
|
|
|
|
1 |
|
||||
A1 |
|
|
|
но α2 +β 2 = |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
, тогда |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
получим |
T |
|||||||
|
|
|
|
k(1-eαt) |
|
|
|
|
|
||||||
|
|
|
|
Т= |
1 |
; |
ξ = −αT . |
|
|
|
|
||||
V(ω)τ=2π/β |
|
|
α 2 + β 2 |
|
t |
|
|
|
|
||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω= |
|
|
|
|
|
Рис. 4.15 |
|
|
|
|
|||||
|
|
|
ω=0 |
U(ω) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Частотные характеристики |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
ω=1/T |
W ( jω) = |
|
k |
2 2 |
+2ξTjω+1 |
||
|
|
−T ω |
