
u_lectures
.pdf
23
Подставим (2.9) в (2.8)
c x |
0 |
σ′′ |
+c x |
0 σ′+c x 0 |
σ= b x 0 |
ϕ′+b x 0 |
ϕ |
(2.10) |
||||||||||||||||
2 |
2 |
|
1 |
2 |
|
|
|
|
0 |
2 |
|
|
1 |
1 |
|
|
0 |
1 |
|
|
||||
Разделим (2.10) на c x |
0 |
и получим с учетом новых обозначений: |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T 2 |
p2 |
+T p +1) σ = (K |
2 |
p + K ) ϕ |
|
|
|
|
|
|
|
(2.11) |
||||||||||||
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
c |
|
|
|
b x 0 |
|
|
|
b x 0 |
|
|
d |
|
|
|
|
||||
T 2 = 2 |
, |
T = |
1 |
, |
K |
|
= |
1 |
1 |
, |
K |
= |
0 |
1 |
, |
p = |
|
. |
|
|
|
|||
|
2 |
c x 0 |
c x 0 |
dt |
|
|
|
|||||||||||||||||
2 |
c |
|
1 |
|
c |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
0 |
|
|
|
|
0 |
|
2 |
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
Уравнение (2.11) можно преобразовать |
|
|
|
|
|
|
|
|
||||||||||||||||
(T 2 p2 |
+T p +1) σ = K (T p +1) ϕ |
|
|
|
|
|
|
|
|
|
(2.12) |
|||||||||||||
2 |
|
|
1 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где T3 = K2 ,
K1
Ti – постоянная времени звена, [c],
K1– коэффициент усиления (безразмерный).
Решая уравнение (2.12) как линейное, можно получить закон изменения выходной величины σ в функции времени σ =σ(t) .
Пример линеаризации звена.
Дана нелинейная функция z = x y , в статике z0 = x0 y0
Образуем функцию F = x y − z =0.
Разложим функцию в ряд Тейлора
|
∂F |
|
|
∂F |
|
∂F |
Δz = 0 , |
|
|
Δx + |
|
Δy + |
|
||
|
∂x 0 |
|
|
∂y 0 |
|
∂z 0 |
|
y0 x + x0 |
y −1 |
z = 0. |
|
|
|||
Откуда получим уравнение в отклонениях z = y0 x + x0 y .

24
3. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ СИСТЕМЫ
Динамическое звено – это устройство любого вида и принципа действия, описываемое определенным дифференциальным уравнением.
Свойства звена могут быть определены различными характеристиками: передаточной функцией, временными характеристиками и частотными характеристиками.
3.1. Передаточная функция звена
Пусть дано динамическое звено.
x1(t) x2(t)
Рис. 3.1
Дифференциальное уравнение такого звена можно записать следующим образом:
a0 |
d n x |
+a1 |
d n−1 x |
+a2 |
|
d n−2 |
x |
+K+an x2 |
= |
|||||||||
|
|
2 |
|
|
|
2 |
|
|
2 |
|
||||||||
|
|
dtn |
|
|
dtn−1 |
dtn−2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
|||||||
|
|
|
d m x |
|
|
|
d m1 − x |
|
|
|
|
|
|
|||||
= b |
|
|
+b |
|
|
+K+b |
x |
|
|
|||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|||||||||
0 |
|
dtm |
|
1 |
|
dtm−1 |
|
|
|
m |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Применим преобразование Лапласа, тогда уравнение (3.1) можно записать:
A1 ( p) X2 ( p) + A2 ( p) = B1 ( p) X1 ( p) + B2 ( p) , |
|
|
|
(3.2) |
||||||||
Правила преобразования Лапласа для производных: |
|
|
|
|||||||||
Если |
f (t) = F( p), то |
|
|
|
|
|
|
|
|
|||
df (t) |
= p F( p) − f (0) , |
|
|
|
|
|
|
|
|
|||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
d n ( f (t)) |
|
n |
|
n−1 |
|
n−2 |
|
|
n−1 |
|
|
|
dtn |
= p |
|
F( p) − p |
|
f (0) + p |
|
f (0) |
+K+ f |
|
(0) |
. |
|
Тогда в уравнении (3.2)
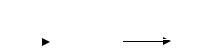
25
A1( p) = a0 pn +a1 pn−1 +K+an ,
A2 ( p) = (a0 pn−1 + a1 pn−2 +K+ an−1 ) x2 (0) −(a0 pn−2 + a1 pn−3 +K+ an−2 ) x2′(0) −
−K−a0 x2n−1 (0)
B1( p) = b0 pm +b1 pm−1 +K+bm ,
B2 ( p) = (b0 pm−1 +b1 pm−2 +K+bm−1 ) x1 (0) −(b0 pm−2 + b1 pm−3 +K+ bm−2 ) x1′(0) −K
−b0 x1m−1(0)
Из уравнения (3.2) выразим X2 ( p) |
|
|||||
X2 ( p) = |
B1 |
( p) |
X1( p) + |
B2 ( p) − A2 ( p) |
(3.3) |
|
A1 |
( p) |
A1( p) |
||||
|
|
|
||||
Первая составляющая представляет собой эффект действия входного сигнала на звено. Вторая составляющая учитывает начальные условия входной и выходной величин.
Пусть при |
|
t = 0 |
x = x ′(t) = x ′′(t) =K= 0 , |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
2 |
= x ′ |
(t) = x ′′(t) =K= 0 . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
Тогда A2 ( p) = 0 и B2 ( p) = 0, а значит уравнение (3.3) примет вид |
|
|||||||||||||||||
|
|
|
X2 |
( p) = |
B1 ( p) |
X1( p) |
|
|
|
|
(3.4) |
|||||||
|
|
|
A1 ( p) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
2 |
( p) |
= |
|
b pm +b pm−1 |
+K+b |
|
|
=W ( p) |
(3.5) |
|||||||
|
|
|
|
0 |
1 |
|
|
|
|
m |
|
|||||||
|
X |
|
( p) |
|
pn + a pn−1 |
|
|
|||||||||||
|
1 |
|
|
a |
0 |
+K+ a |
n |
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
Выражение (3.5) называется передаточной функцией звена.
Таким образом, передаточной функцией звена (или системы) называется отношение изображений выходной и входной величин при нулевых начальных условиях.
С физической точки зрения W ( p) можно представить как динамический, т.е., переменный во времени коэффициент передачи звена.
Выражение (3.5) можно представить графически (рис. 3.2).
X1( p) |
|
|
X |
2( p) |
|
W ( p) |
|||||
|
|
|
|
||
|
|
|
|
|
26
Рис. 3.2
3.2. Временные характеристики динамических звеньев
Динамические свойства звена могут быть определены по его переходной функции или по импульсной функции (функции веса).
Переходная функция h(t) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход ступенчатого воздействия типа единичной ступенчатой функции.
Если входное воздействие представляет собой неединичную
x1
x1=1(t
1
0
ступенчатую функцию
|
|
x2 |
1(t)= |
0 при t≤0 |
x2(t)=h |
1 при t>0 |
|
|
|
|
t |
Рис. 3.3 |
0 |
|
t |
x1(t) = N 1(t) , то выходная величина x2 (t) = N h(t).
Ступенчатая функция часто встречается при анализе САУ. Примером функции 1(t) может служить: мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, управляющие воздействия, подаваемые на вход системы оператором.
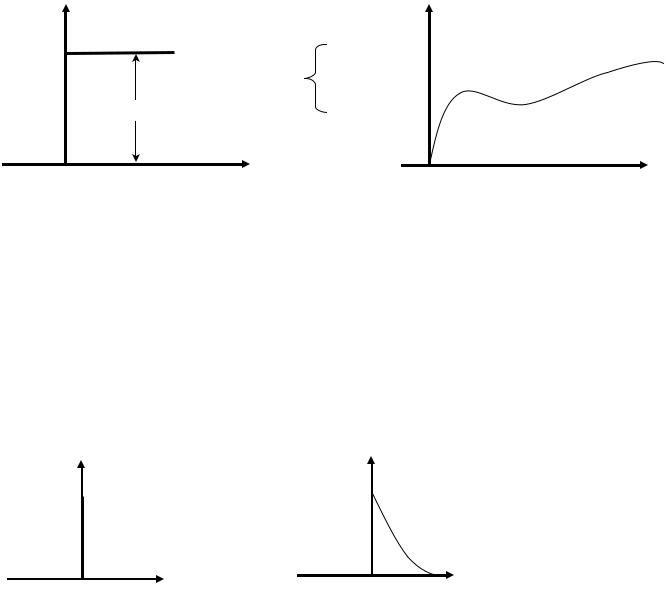
Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход.
Единичная импульсная функция, или дельта-функция, это производная от единичной ступенчатой функции δ (t) =1′(t) . Дельта-функция δ(t) равна
нулю везде, кроме точки t = 0, где она стремится к бесконечности.
X1 |
X2 |
δ(t)
w(t) –функция веса
0 |
t |
Рис. 3.4 |
0 |
t |
|
|
|
|
+∞
Основное свойства δ(t): ∫ δ(t) dt =1, т.е. она имеет единичную площадь.
−∞
27
Пример δ(t). Кратковременный ток короткого замыкания в генераторе, кратковременная нагрузка на валу двигателя.
Связь между h(t) и w(t).
Воспользуемся дифференциальным уравнением звена в операторной форме
A(D) xвых (t) = B(D) xвх (t) . |
|
|||
Пусть xвх (t) =1(t) , тогда |
|
|||
A(D) h(t) = B(D) 1(t) . |
(3.6) |
|||
Продифференцируем (3.6) по t и получим |
|
|||
′ |
|
|
||
A(D) h (t) = B(D) δ (t) , но так как |
|
|||
A(D) w(t) = B(D) δ (t) , то следует, что |
|
|||
′ |
|
|
||
w(t) = h (t). |
|
|
||
Таким образом, уравнение связи имеет вид |
|
|||
w(t) = |
dh(t) |
или |
(3.7) |
|
dt |
||||
|
|
|
||
t
h(t) = ∫w(τ)dτ .
0
Связь весовой функции с передаточной функцией звена
Для звена справедливо:
X2 ( p) =W ( p) X1( p)
Пусть x1(t) =δ (t) ,тогда x2 (t) =ϖ(t) .
Найдем изображения входной и выходной величин:
X1( p) =δ ( p) =1 , X2 ( p) =ϖ( p) =W ( p) 1.
Откуда следует, что
ϖ(t) ÷W ( p).
Таким образом, ϖ(t) и W ( p) связаны с помощью прямого преобразования
Лапласа
W ( p) = ∞∫ϖ(t)e− ptdt .
0

28
∞
W ( p) = p∫h(t)e− pt dt - связь переходной и передаточной функций.
0
Если входное воздействие x1(t) произвольно то X2 ( p) =W ( p)* X1( p)
и на основании теоремы свертки x2 (t) = ∫t ϖ(t)* x1(t −τ)dτ ,
0
где τ - вспомогательное время интегрирования, изменяющееся в пределах от 0 до рассматриваемого текущего времени t0.
3.3. Частотные характеристики звеньев
Переходные характеристики дают сведения о поведении системы в
переходных режимах. Для оценки установившихся режимов более удобно рассматривать поведение систем при воздействиях, являющихся периодическими функциями времени. Выбор гармонических воздействий обусловлен следующими причинами:
реальные воздействия можно разложить в ряды Фурье,
гармонические воздействия можно легко получить в эксперименте.
|
|
|
|
Пусть на вход звена (рис. 3.5) |
подано гармоническое |
|
x1 |
|
|
x2 |
воздействие |
x1 = X1 cosωt , где X1 |
– амплитуда, ω - угловая |
|
|
|||||
|
|
|
|
|||
|
|
|
|
частота. |
|
|
|
Рис. 3.5 |
|
|
|
||
|
|
|
|
|
||
Тогда на выходе появится также гармонические колебания, имеющие ту же
частоту, но в общем случае сдвинутые по фазе относительно входной величины на угол ϕ, то есть x2 = X2 cos(ωt +ϕ).
Представим x1 и x2 в символической форме
x |
= X e jωt |
(3.8) |
1 |
1 |
|
|
|
|
|
|
|
|
x |
= X |
2 |
e j(ωt+ϕ) |
|
|
|
(3.9) |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
(В символической форме cosωt =e jωt , вместо точного значения |
||||||||||||||||||||
x1 = |
X1 |
(e jωt + e− jωt ) = x1′ |
+ x2′′ - на основании формулы Эйлера). |
|||||||||||||||||
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Чтобы выяснить соотношение между x1 и x2 воспользуемся |
|||||||||||||||||||
дифференциальным уравнением звена |
|
|
|
|
|
|||||||||||||||
|
|
|
d n x |
2 |
|
d n−1x |
2 |
|
|
|
|
|
|
|
d m x |
|
d m−1x |
|
||
a |
|
|
|
|
+ a |
|
+K + a |
n |
x |
|
= b |
1 |
+ b |
1 |
+K + b x |
|||||
0 |
|
dtn |
dtn−1 |
2 |
dtm |
dtm−1 |
||||||||||||||
|
|
1 |
|
|
|
|
0 |
1 |
m 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
29
Продифференцируем (3.8) и (3.9) по t и подставим в (3.10)
dx2 |
= |
X |
ω |
e |
j(ωt +ϕ) ; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
dt |
2 j |
|
|
|
|
|
|
|
d n x2 |
|
|
|
|
|
|
|||
d 2 x2 |
= |
|
|
ω |
2 |
|
j(ωt +ϕ) |
|
K |
|
= |
|
ω |
n |
|
j(ωt +ϕ) ; |
||
dt2 |
|
|
|
|
|
dtn |
|
|
||||||||||
|
X 2 ( j ) |
|
e |
|
, |
|
, |
|
X |
2 ( j ) |
|
e |
|
|||||
dx1 |
= X jωe jωt ; |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dt |
|
|
|
|
1 |
|
|
|
|
|
d m x1 |
|
|
|
|
|||||
d 2 x1 |
|
= X |
1( jω)2 e jωt ,K, |
= X1( jω)m e jωt . |
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||
dt 2 |
|
|
|
|
|
|
|
|
|
dt m |
|
|
|
|
|
|||||
[a |
0 |
( jω)n |
|
+ a ( jω)n−1 +K+ a |
n |
]X |
2 |
e j(ωt+ϕ) |
= |
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(3.11) |
||||
|
|
|
|
|
( jω)m + b ( jω)m−1 +K+ b |
]X e jωt |
|
|
||||||||||||
= |
[b |
|
|
|
|
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
m |
|
1 |
|
|
|
||
|
|
|
|
Из (3.11) получим |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
X 2 |
|
e |
jϕ |
= |
b0( jω)m +b1( jω)m −1 +K+bm |
=W ( jω). |
(3.12) |
|||||||
|
|
|
|
|
|
X1 |
|
|
a0( jω)n |
+ a1( jω)n −1 +K+ an |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
W ( jω) – это комплексное число, модуль которого равен отношению
амплитуды выходной величины к амплитуде входной, а аргумент сдвигу фаз
входной и выходной величин
modW ( jω) = |
|
W ( jω) |
|
= |
X2 |
; |
argW ( jω) =ϕ . |
|
|
||||||
|
|
X1 |
|||||
|
|
|
|
|
|
|
Если в W(p) вместо p подставить jω, то формально можно получить
частотную передаточную функцию. Выражение (3.12) можно представить
W ( jω) = |
A+ jB |
= |
(A+ jB) |
× |
(C − jD) |
= AC + BD |
+ j BC − AD |
=U (ω) + jV , |
C + jD |
|
|
||||||
|
|
(C + jD) (C − jD) |
C2 + D2 |
C2 + D2 |
|
|||
где U(ω) – вещественная составляющая частотной функции; V(ω) – мнимая составляющая частотной функции.
Можно представить W ( jω) и в другой форме, а именно:

30
W ( jω) == A(ω) e jϕ(ω) ,
где W ( jω) = 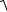 U 2(ω) +V 2(ω) = A(ω) – модуль частотной передаточной функции,
U 2(ω) +V 2(ω) = A(ω) – модуль частотной передаточной функции,
ϕ(ω) = arctg UV ((ωω)) – фаза частотной передаточной функции.
Для наглядного представления частотных свойств звена применяются так называемые частотные характеристики.
3.3.1. Амплитудно-фазовая частотная характеристика
Строится на комплексной плоскости. Представляет собой геометрическое место концов векторов (годограф), соответствующих
частотной |
передаточной |
функции |
W ( jω) =U (ω) + jV (ω) |
|
при |
|||||
изменении ω от 0 до ∞. |
|
|
1 |
|
||||||
Пример. Пусть дана частотная передаточная функция W ( jω) = |
|
|||||||||
Tjω+1 |
||||||||||
|
V |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
–ω2 |
|
|
|
|
|||
|
|
|
|
|
–ω1 |
|
|
|
||
|
|
|
|
U |
|
|
|
|||
ω→– |
|
|
|
|
U(ω1) |
|
|
|
||
|
|
|
|
|||||||
|
|
|
ω=0 |
|
|
|
||||
ω→∞ |
|
ϕ(ω1) |
|
|
|
|
||||
V(ω1) |
A(ω1) |
|
|
|
|
|||||
|
|
ω1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
ω2 |
|
|
|
|
|||
|
|
|
Рис.3.6 |
|
|
|
|
|||
Основные свойства:
1)Число квадрантов, где проходит АФХ не выше, чем порядок дифференциального уравнения;
2)АФХ, построенные при изменении ω от 0 до +∞ и от 0 до -∞, симметричны.
3)Можно построить зависимости модуля и фазы от частоты (рис. 3.7).
A |
|
|
ϕ |
|
|
|
|
0 |
ω |
|
|
|
|
|
а) |
ω |
|
–90° |
б) |
|
|
|
||
Рис. 3.7 |
|
|||

31 |
|
3.3.2. Логарифмические частотные характеристики |
|
Пусть задана частотная передаточная функция |
|
W ( jω) = A(ω) e jϕ(ω) |
(3.13) |
Прологарифмируем (3.13)
lnW ( jω) =ln A(ω) + jϕ(ω) ,
то есть логарифм W(jω) – это комплексное выражение, где действительная часть– ln модуля, а мнимая часть– фаза.
Для практических целей удобно пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (ЛАХ) и логарифмическую фазовую частотную характеристику (ЛФХ).
Для построения ЛАХ находится величина
L(ω) =20lgW ( jω) =20lg A(ω).
L(ω) – измеряется в децибелах [дБ].
Бел – это такое усиление, когда мощность увеличивается в 10 раз (1Б=10дБ) 2 Бела – усиление в 100 раз.
Крупные единицы: декабелы, гектобелы и т. д. Мелкие единицы: децибелы, сантибелы и т. д.
Так как мощность сигнала пропорциональна квадрату его амплитуды (например, P ≈ I 2 ), то при усилении, равном 1Б, величина
lgW ( jω) 2 = 2lgW ( jω) равна 1, при усилении, равном 2Б, эта величина равна
2 и т. д.
Следовательно, усиление амплитуды в Б, численно равно 2lgW ( jω) , а усиление в децибелах, численно равно 20lgW ( jω) .
|
|
P |
|
|
|
|
|
U 2 |
|
|
U |
2 |
|
|
|
|
|||||
L(ω) =10lg |
2 |
[дБ] |
=10lg |
2 |
|
=20lg |
|
|
[дБ] |
|
|
||||||||||
|
P1 |
U12 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
U1 |
|
|
|
|||||
|
P |
|
|
|
U |
2 |
|
|
U |
2 |
|
|
|
|
|
U |
2 |
|
|||
L(ω) =lg |
2 |
|
[Б] =lg |
|
|
|
= 2lg |
|
|
[Б] |
= 20lg |
|
[дБ]. |
||||||||
P |
|
|
|
2 |
U |
U |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
U1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
По оси абсцисс откладывается частота ω в логарифмическом масштабе, то есть наносятся отметки, соответствующие lgω, а около них пишется само значение частоты ω, [рад/сек].
Единицами измерения ω являются октава и декада.
32
Декада – это интервал частот, заключенный между произвольным значением ω и 10ω.
lg10ω−lgω=lg10=1, то есть отрезок между ω и 10ω не зависит от
абсолютного значения ω.
Октава – интервал частот, заключенный между произвольным значением ω и 2ω.
lg 2ω−lgω=lg 2 , тоже не зависит от абсолютного значения ω.
ϕ° |
|
L,дБ |
|
|
|
|
|
|
|
|
|
|
|
Рекомендуемый |
|
60° |
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
40° |
|
20 |
|
|
|
декада |
|
|
|
|
декада |
|
|
1 декада – 50 мм |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
20° |
|
|
|
|
|
|
|
|
ω,1/сек |
1 дБ – 2 мм |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-20° |
|
|
1 |
2 |
|
4 |
10 |
20 |
40 |
100 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1° – 1 мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-40° |
|
|
|
|
октава |
|
|
|
|
|
октава |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-60°
Рис. 3.8
Практически для нанесения логарифмического масштаба можно пользоваться выражением:
mω [мм] = mдек [мм] lgω ,
где: ω – угловая частота, mдек – длина декады в миллиметрах, mω –длина
отрезка от начала декады до заданной частоты. Достоинства логарифмического масштаба:
•Могут быть нанесены на график несоизмеримые значения амплитуды и частоты;
•ЛАЧХ являются прямолинейными;
•Основное достоинство ЛАЧХ в том, что их построение почти не требует вычислительной работы. Это особенно заметно, когда W(jω) может быть представлена в виде произведения сомножителей.
W ( jω) =W1( jω) W2( jω) ;
W ( jω) = A1(ω)e jϕ1(ω) A2(ω)e jϕ2 (ω) = A1(ω) A2(ω) e j[ϕ1(ω)+ϕ2(ω)] ,
то есть логарифмические частотные характеристики можно получить суммированием ординат отдельных ЛАХ.
L(ω) =20lg A1(ω) lg A2(ω)
L(ω) =20lg A1(ω) +20lg A2(ω)
ϕ(ω) =ϕ1(ω) +ϕ2(ω)
