u_lectures

113

Тогда (11.17) перепишем в виде:

x&1 = x2x&2 = x3

...........

x&n-1 = xn

x&n = a1 (U - a1xn - ...- an-1x2 - an x1 )

0

(11.18)

Уравнение (11.13)можно представить:

Y(p)= b0 pm X(p)+b1 pm-1 X(p)+…+bm X(p)

(11.19)

Применим обратное преобразование Лапласа к (11.19)

y = b0 xm +b1x(m-1) +…+bm x .

(11.20)

С учетом равенств (11.17) запишем (11.20) в виде:

y = b0 xm+1 +b1xm +…+bm x1 .

(11.21)

Уравнения состояния (11.18)и (11.21) можно представить в векторно-матричной форме:

117

x&(t)= Ax(t)+ Bu(t),

(11.26)

y(t)= Cx(t)+ Du(t),

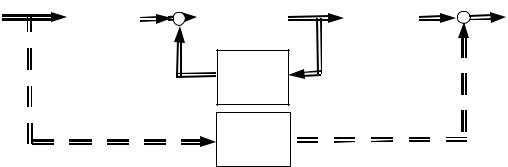
Тогда можно изобразить матричную структурную схему (рис. 11.4), где двойные стрелки соответствуют векторным величинам.

A

D

Рис. 11.4. Матричная структурная схема

2. Характеристическое уравнение системы.

По уравнениям состояния стационарных систем можно найти характеристическое уравнение в виде

[pI − A] = 0

pn + a1 pn−1 +K+ an = 0 .

(11.27)

Корни уравнения (11.27) соответствуют полюсам системы и называются собственными или характеристическими числами матрицы А. Корни

118

уравнения (11.27) определяют устойчивость системы, отсюда следует, что только матрица А определяет устойчивость системы.

3. Определение передаточной матрицы объекта управления по уравнениям состояния.

Пусть уравнения состояния имеют вид (11.26).

Используя преобразование Лапласа, получим:

pX(p)- x(0)= AX(p)+BU(p)

Y(p)=CX(p)+DU(p)

( 1 1 . 2 8 ) ( 1 1 . 2 9 )

Допустим, что начальные условия нулевые, т.е. x(0)= 0 , а также будем считать, что матрица D = 0, тогда перепишем уравнение (3) в виде:

[pI - A]X(p)= BU(p)

(11.30)

откуда выразим Х(р):

X(p)= [pI - A]-1 BU(p)

(11.31)

Подставим это выражение в уравнение (11.29):

Y(p)= C[pI - A]-1 BU(p).

(11.32)

119

Тогда из (11.32) следует, что передаточная матрица между вектором входных и выходных переменных будет равна:

W(p)= C[pI - A]-1 B

(11.33)

Обратную матрицу [pI - A]-1 в (11.33) определяют по выражению:

[pI - A]-1 = adj(pI - A) , /pI - A/

(11.34)

где /pI - A/ - определитель матрицы (pI-A),

adj(pI - A) - присоединенная матрица, которая получается

транспонированием матрицы, составленной из миноров каждого элемента матрицы (pI - A), взятых со знаком (-1)i+ j (i, j - номера строк и столбцов).

120

12. СИНТЕЗ МОДАЛЬНЫХ РЕГУЛЯТОРОВ

Задача синтеза автоматических систем занимает центральное место в теории управления. Современный подход к решению этой задачи базируется на математическом описании в виде уравнений пространства состояний.

121

Существует несколько подходов для решения этой задачи.

1.Составляют функционал от функции состояния и управления, накладывают физические ограничения на эти функции и на основе вариационного исчисления определяют оптимальное управление, минимизирующее исходный функционал. Этот раздел ТАУ – называется оптимальное управление и разработан Понтрягиным Л.С.

2.Существует подход, называемый аналитическое конструирование регуляторов. В этом случае при заданной структуре объекта и регулятора на основе заданного функционала, отражающего требование к системе, определяются параметры регулятора, обеспечивающие минимум функционала. Задача может быть решена на ЭВМ с помощью методов поисковой оптимизации: градиентного, симплексного и т.д.

3.Наряду с этими общими подходами разработаны методы синтеза замкнутых систем непосредственно по заданным динамическим

Это направление современной теории получило широкое распространение в инженерной практике, т.к. эти регуляторы реализуемы и могут быть синтезированы на ЦВМ и аналитически.

Модальное управление – это методы формирования цепей обратных связей, придающих замкнутой системе заранее выбранное расположение корней характеристического уравнения.

(Происхождение термина: корням характеристического уравнения соответствуют составляющие свободного движения системы, называемые иногда модами).

Обычно задаются желаемым характеристическим полиномом замкнутой системы (т.е. знаменателем передаточной функции замкнутой системы). Существует несколько типовых форм полиномов, из них наиболее употребительны следующие.

Форма Баттерворта Биномиальная форма

122

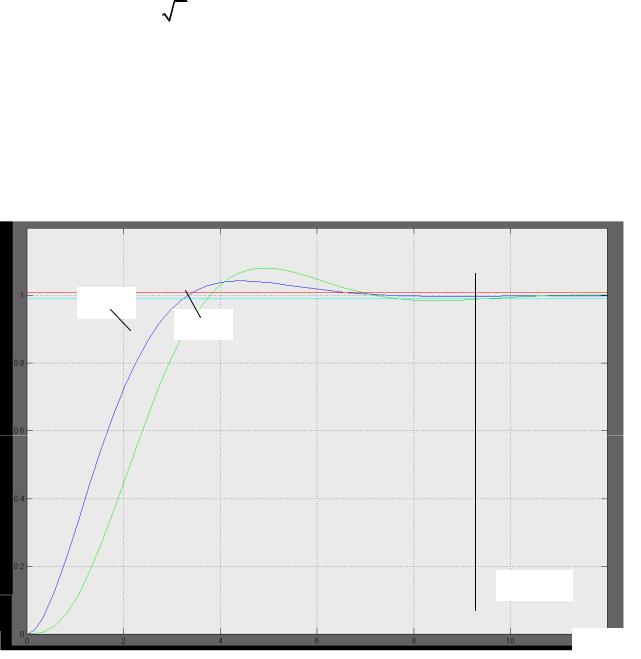
Эти полиномы минимизируют интегральные критерии различного вида, здесь ω0 - постоянная, выбираемая исходя из желаемого быстродействия. Для фильтра Баттерворта нормированный переходный процесс имеет вид:

x

n =2

n =3

tp =9.5

ω0 tp

Рис. 12.1.Переходный процесс для фильтра Баттерворта

По оси абсцисс откладывается относительное время переходного процесса. Если n= 3, то при ω0 ×tn = 9.5 переходный процесс закончен

(при величине зоны – 1%).

Пусть задано tn =0.2 c , тогда