
u_lectures
.pdf103
Т.е. f1 дает статическую ошибку, а f2 не дает.
10.2. Коэффициенты ошибок
Пусть на входе системы действует сигнал g(t) произвольной формы. Найдем изображение сигнала ошибки.
X ( p) = ΦX ( p)G( p) = |
|
|
G( p) |
, |
(10.6) |
|
1 |
+W ( p) |
|||||
|
|
|
||||
где ΦX ( p) – передаточная функция замкнутой системы по ошибке, G( p) – изображение сигнала g(t) .
Разложим ΦX ( p) в ряд по возрастающим степеням p
X ( p) = |
c0 |
+c1 p + |
c2 |
p2 + |
c3 |
p3 +K G( p) , |
(10.7) |
|
|
||||||
|
|
2! |
3! |
|
|
||
|
|
|
|
||||
сходящийся при малых значениях p, то есть при больших значениях времени t, что соответствует установившемуся процессу при заданном g(t) .
Перейдем в (10.7) к оригиналу и получим формулу для установившейся ошибки
|
|
X |
уст |
= c |
g(t) + c |
dg(t) |
+ |
c |
2 |
|
d 2 g |
(t) |
|
+K |
. |
(10.8) |
|||||||
|
|
dt |
|
2! |
dt 2 |
|
|||||||||||||||||
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
||||||||||
Величины c0 , c1 , c2 ,… – коэффициенты ошибок, которые проще всего |
|||||||||||||||||||||||
определить, |
если числитель |
|
ΦX ( p) разделить на знаменатель и сравнить |
||||||||||||||||||||
полученный ряд с выражением (10.7). |
|
|
|
|
1 |
|
|
||||||||||||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
≠ 0 в статических системах c |
0 |
= |
|
|
|
, |
|
|||||||||||||||
1 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ K |
|
|||||
c0 |
= 0 , c1 ≠ 0 в астатических системах 1-го порядка, |
|
|||||||||||||||||||||
c0 |
= 0 , c1 = 0 , c2 ≠ 0 в астатических системах 2-го порядка |
|
|||||||||||||||||||||
Пример: |
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
WP ( p) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p(Tp +1) |
|
|
p(Tp +1) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ΦX ( p) = |
|
|
1 |
|
= |
|
|
|
|
|
|
|
|
||||||||||
1 |
+WP ( p) |
p(Tp +1) + K |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
p +Tp2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
K + p +Tp2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
1 |
3 |
|||||||||||||||||||
|
p + |
|
|
|
|
p |
|
|
+ |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p + |
|
|
|
|
|
T − |
|
|
|
|
|
|
p |
|
|
+ |
|
|
|
− 2T + |
|
p |
|
||||||||||||||||
|
K |
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
K |
|
|
|
|
|
|
|
|
K |
2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
K |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
T |
|
p |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
T − |
|
|
|
p |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
T |
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
T − |
|
|
|
p |
|
|
+ |
|
|
|
|
|
|
T − |
|
|
|
|
p |
|
|
+ |
|
|
|
|
T |
− |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
K |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
T |
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2T |
+ |
|
|
|
|
p |
|
|
− |
|
|
|
|
T |
− |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2T |
+ |
|
|
|
|
p |
|
|
+K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Таким образом, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ΦX ( p) = |
|
|
|
|
|
p + |
|
|
|
|
|
|
T |
− |
|
|
|
|
p |
|
|
|
+ |
|
|
|
|
|
|
− |
2T + |
|
|
|
|
|
p |
|
+K |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K 2 |
|
|
K |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Откуда коэффициенты ошибок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
c0 = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c = |
1 |
, с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= |
|
|
|
|
T − |
|
|
|
|
|
, с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
K |
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
c3 |
|
|
|
1 |
|
|
− 2T |
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
, с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6 |
|
K 2 |
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10.3. Повышение степени астатизма
Системой с нулевым порядком астатизма или статической по данному воздействию называется система, у которой при g = g0 = const ошибка x
пропорциональна величине g0 . Это возможно только при c0 ≠ 0 .
Системой с астатизмом первого порядка называется система, у которой x = 0 при g = g0 + g10t постоянна и пропорциональна g10 . Это возможно, если
c0 = 0 , c1 ≠ 0 .
Системой с |
астатизмом |
второго |
порядка |
называется система, у |
|||||||
которой x = 0 при |
g = g |
0 |
+ g |
10 |
(t) , а при |
q = q |
0 |
+ q |
t + |
q20t 2 |
пропорциональна |
|
|||||||||||
|
|
|
|
|
10 |
2! |
|
||||
|
|
|
|
|
|
|
|
|
|
||
величине q20 .
Рассмотрим структурный признак астатизма.
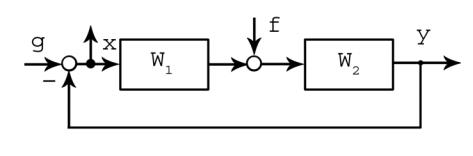
Пусть имеем систему (рис. 10.4).
105
Рис. 10.4
Порядок астатизма по отношению к рассматриваемому воздействию f
равен числу интегрирующих звеньев, включенных в цепь обратной связи W1 ( p) между точками приложения воздействия (входом) и измерения
ошибки (выходом) и не зависит от числа интегрирующих звеньев, включенных в цепь прямого преобразования сигнала.
Для управляющего воздействия весь контур системы представляет собой обратную связь.
Пример:
W |
( p) = |
Ku |
; W |
( p) = |
W0 |
= |
1 |
|
|
K |
. |
|
|
|
|
|
|
|
|||||||
1 |
|
p |
2 |
|
p p T 2 p2 |
+ 2ξTp +1 |
|
|||||
|
|
|
|
|
||||||||
Из структурной схемы следует, что:
система является астатической 2-го порядка по управляющему воздействию,
система является астатической 1-го порядка по возмущающему воздействию.
11. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ САУ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
1.1. Описание систем в виде уравнений пространства состояний
Классическая теория использует, главным образом, аппарат передаточных функций и частотных характеристик. В последние десятилетия сформировался раздел, получивший название «современная теория управления».
106
Ее главной особенностью является рассмотрение систем во временной области на основе понятия пространства состояний. При этом рассматриваются в общем случае многомерные системы со многими входами и выходами, в связи с чем широко используется язык векторноматричных уравнений и аппарат линейной алгебры. Фундаментальным понятием современной теории управления является понятие состояния.
Состояние системы в момент времени t0 , есть такая минимальная совокупность сведений о ней, которая вместе с входным воздействием, заданным на интервале времени t0 ≤ t ≤ t1 , позволяет прогнозировать
поведение системы в любой точке этого интервала [1].
САУ можно описать в общем случае системой нелинейных дифференциальных уравнений первого порядка в форме Коши.
Для более узкого, но широко распространенного класса систем , т.е. для линейных стационарных систем уравнения состояния можно записать в векторно-матричной форме:
x(t) |
= |
Ax(t) |
+ |
Bu(t), |
(11.1) |
& |
|
|
|||
y(t) =Cx(t) + Du(t), |
(11.2) |
||||
x1(t)
где x(t) = . – n- мерный вектор состояния;
.xn (t)
u1 (t)
u(t) = . – к- вектор входных воздействий;
.uk (t)
107
y1 (t) |
|
|
. |
|
– m- вектор выходных величин; |
y(t) = |
|
|
. |
|
|
|
|
|
ym (t) |
|
|
a11
A = ..an1
. . |
a1n |
|
. . |
. |
|
. . |
. |
|
|
||
. . |
|
|
ann |
||
– матрица системы размера n× n, характеризует динамические свойства системы;
b11
B = ..bn1
c11
C = ..cm1
. . |
b1k |
|
. . |
. |
|
. . |
. |
|
|
||
. . |
|
|
bnk |
||
. . |
c1n |
|
. . |
. |
|
. . |
. |
|
|
||
. . |
|
|
cmn |
||
– матрица управления размера n× k, характеризует воздействие входных величин uj на переменные состояния xi ;
– матрица измерения размера m× n, характеризует связь выходных координат yk с переменными состояния xi.
Матрица D имеет размерность m× k и в электромеханических системах обычно равна нулю.
108
Уравнения состояния могут быть составлены:
•по структурной схеме системы;
•по известной передаточной функции системы.
11.2. Запись уравнений состояния по структурной схеме
При составлении уравнений состояния по структурной схеме в качестве переменных состояния чаще всего выбираются реальные физические переменные (напряжение, ток, скорость и т.д.). Иногда целесообразно в качестве переменных состояния выбрать некоторые фиктивные переменные, отличающиеся от выходных величин реальных звеньев. Для упрощения записи уравнений состояний желательно преобразовать схему так, чтобы она состояла из интегрирующих и усилительных звеньев.
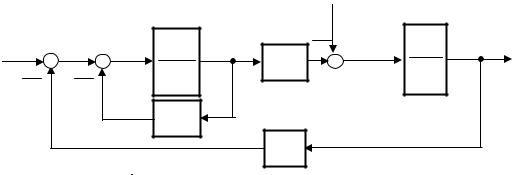
Рассмотрим в качестве примера двигатель постоянного тока, имеющий структурную схему (рис. 11.1).
Входные величины: U я– управляющее воздействие и Мс – возмущающее воздействие. В качестве выхода рассмотрим скорость ω.
В качестве переменных состояния выберем переменные на выходах инерционных звеньев ток якоря – I и частоту вращения вала якоря – ω.
|
|
|
|
МC |
UЯ |
xВХ2 |
1 |
I |
xВХ1 |
|
|
LЯ p |
|
kМ |
|
|
|
|
RЯ
kЕ |
1 ω
J p
109
Рис.
Рис. 11.1. Структурная схема двигателя постоянного тока
Преобразование передаточных функций элементов структурных схем в дифференциальные уравнения в форме Коши приведено в прил. 3 [1].
Запишем дифференциальные уравнения для апериодического и интегрирующего звеньев, используя вспомогательные переменные
xВХ1 и xВХ 2 :
|
& |
|
-1 |
xВХ1 |
; |
|
|
||
ω= J |
|
|
|
(11.3) |
|||||
|
& |
-1 |
(x |
|
- R |
|
|||
I = L |
|
ВХ2 |
Я |
I). |
|||||
|
|
Я |
|
|
|
|
|||
Для исключения вспомогательных переменных xВХ1 и xВХ2 , выразим их
через переменные состояния и входные величины непосредственно из структурной схемы на рис. 11.1:
|
= kМ I - MC ; |
|
||
xВХ1 |
(11.4) |
|||
x |
=U |
- k ω. |
||
|
||||
|
Я |
E |
|
|
ВХ2 |
|
|||
Подставим (11.4) в исходную систему (11.3):
|
|
|
kM |
|
|
|
|
1 |
|
|
|
|
|
|
|||
ω= |
|
|
|
I - MC |
|
|
, |
|
|
|
|
|
|||||
|
& |
|
|
J |
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.5) |
||||
|
|
|
|
kE |
|
|
RЯ |
|
|
1 |
|
|
|||||
I& |
= - |
|
ω- |
I + |
U |
Я |
. |
||||||||||
|
|
|
L |
|
|||||||||||||
|
|
|
|
L |
Я |
|
|
L |
Я |
|
|
|
Я |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение выхода
|
110 |
y = ω. |
(11.6) |
Особенности полученных уравнений состояния:
•их два – по числу переменных состояния в системе второго порядка;
•они являются дифференциальными, в левых частях, которых находятся производные переменных состояния;
•правые части зависят только от переменных состояния и от входных воздействий;
•уравнение выхода алгебраическое.
Перепишем уравнения (11.5), добавив для наглядности нулевые слагаемые:
|
|
|
|
|
kM |
|
|
|
|
|
1 |
|
|||
ω = 0 ω + |
|
|
I |
+ 0 U Я − |
|
|
M C , |
||||||||
|
& |
|
|
|
J |
|
|
|
|
|
|
J |
|
||
|
|
|
|
|
|
|
|
|
|
(11.7) |
|||||
|
|
|
kE |
|
|
RЯ |
|
1 |
|
|
|
||||
I& |
= − |
ω − |
I + |
U |
Я + 0 M C . |
||||||||||
|
|
|
|||||||||||||
|
|
|
LЯ |
|
|
LЯ |
|
|
LЯ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Запишем уравнения (11.7) и (11.6) в векторно-матричной форме
|
|
0 |
|
k |
M |
|
|
|
|
0 |
|||
ω |
|
|
|
|
|
|
ω |
|
|||||
|
|
J |
|||||||||||
& |
= |
|
|
|
|
|
|
|
× |
+ |
|
||
|
|
kЕ |
|
|
RЯ |
1 |
|||||||
I& |
|
- |
- |
|
I |
|
|||||||
|
|
|
|||||||||||
|
|
|
LЯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LЯ |
|
LЯ |
||||||
1 |
|
|
|
|
- |
|
|
UЯ |
|
J |
, |
|||
|
|
× |
||
0 |
|
MС |
|
|
|
|
|
||
|
|
|
|
|
y = 1 ω +0 |
I = [1 0]× ω . |
|
I |
(11.8)
(11.9)
Из уравнений (11.8) и (11.9) получим матрицы, входящие в уравнения состояния (11.1) и (11.2):

111
|
0 |
|
kМ |
|
|
|
0 |
- |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
J |
|
|
|
||||||||
|
|
|
|
J |
, C = [1 0], D = [0 0]. |
||||||||
A= |
|
|
|
|
, |
B = |
|
|
|
|
|||
kЕ |
|
|
RЯ |
1 |
|
|
|
||||||
- |
- |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|||||||||
|
L |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
LЯ |
|
|
|
|
|
|||||
|
Я |
|
|
Я |
|
|
|
|
|
|
|
||
1.3. Составление уравнений состояния по известной передаточной функции
При записи уравнений состояния по известной передаточной функции существует несколько основных форм уравнений состояния (канонические формы
1,2 и 3-го типа).
Наиболее простым является метод фазовых переменных, он применяется в одномерном случае, т.е. для систем с одним входом и одним выходом.
Пусть известна передаточная функция системы:
Y(p) |
|
b pm +b pm-1 |
+ ...+b |
||
0 |
1 |
m , |
|||
W(p)= U(p) |
= |
|
|
||
a0 pn + a1 pn-1 + ...+ an |
|||||
(11.10)
где m<n.
Уравнение (11.10) умножим на U(p)B(p) , тогда получим
Y(p) U(p) =
(b0 pm +b1 pm-1 + ...+bm )= (a0 pn + a1 pn-1 + ...+ an ) X ( p).
(11.11)
где Х(р) – новая переменная.
Тогда равенство (11.11)можно представить в виде 2-х уравнений:

112
(a0 pn + a1 pn-1 |
+...+ an )X(p)= U(p) |
(11.12) |
|
|
|
|
+...+bm )X(p)= Y(p) |
|
(b0 pm +b1 pm-1 |
(11.13) |
|
|
|
|
Рассмотрим уравнение (11.12).
Изменяя порядок слагаемых и, выразив старшую производную, получим:
pn X(p)= |
1 |
U(p)- a pn-1 X(p)-…- a |
n-1 |
pX(p)- a X(p) . |
(11.14) |
|||
a |
||||||||
|
|
1 |
n |
|
|
|||
|
0 |
|
|
|
|
|
|
|
Применим к (11.14)обратное преобразование Лапласа
x |
(n) |
= |
1 |
U - a x |
(n-1) |
-…- a x′ - a x |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
n-1 |
n |
|
(11.15) |
a0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Введем фазовые переменные, которые представляют собой переменную х и ее производные вплоть до (n - 1).
x1 = x
x2 = x&
x3 = &&x
..........
xn -1 = x(n -2)xn = x(n -1)
x1 |
= x = x2 |
|
& |
& |
|
& |
&& |
(11.17) |
x2 |
= x = x3 |
|
x3 = x4 |
|
|
& |
|
|
...........
x&n-1 = xn
x = x(n) = правая_часть_(11.15)
&n
