u_lectures

213

X2

С

X1

Рис. 26.13

26.5.Основные виды соединений нелинейных звеньев

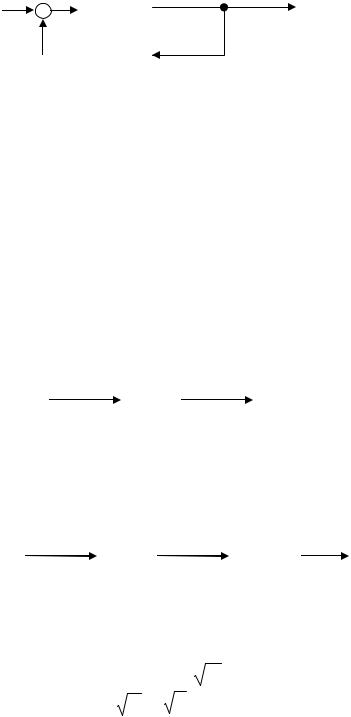
1)Последовательное соединение.

Рис. 26.14

Сигнал “y” на выходе из системы

Пусть в обоих случаях входные сигналы “x” равны, тогда из (26.1) и (26.2) следует, что выходные сигналы не равны.

Следовательно, при последовательном соединении нелинейных звеньев не выполняется принцип коммутативности, поэтому НЗ нельзя менять местами.

2) Параллельное соединение

214

Рис. 26.16

x = x1 = x2

y = y1 + y2 = F(x1) + F(x2)

3) Встречно– параллельное соединение звеньев.

Рис. 26.17

y = F1( x1) = F1( x – y2 ) = F1[ x - F2(y)]

Выходная величина выражена в этом случае неявно.

26.6. Способы нейтрализации нелинейных звеньев

Нейтрализация нелинейных звеньев применяется для того, чтобы исключить нелинейные звенья и приблизить систему к линейному виду.

Существует 2 способа нейтрализации

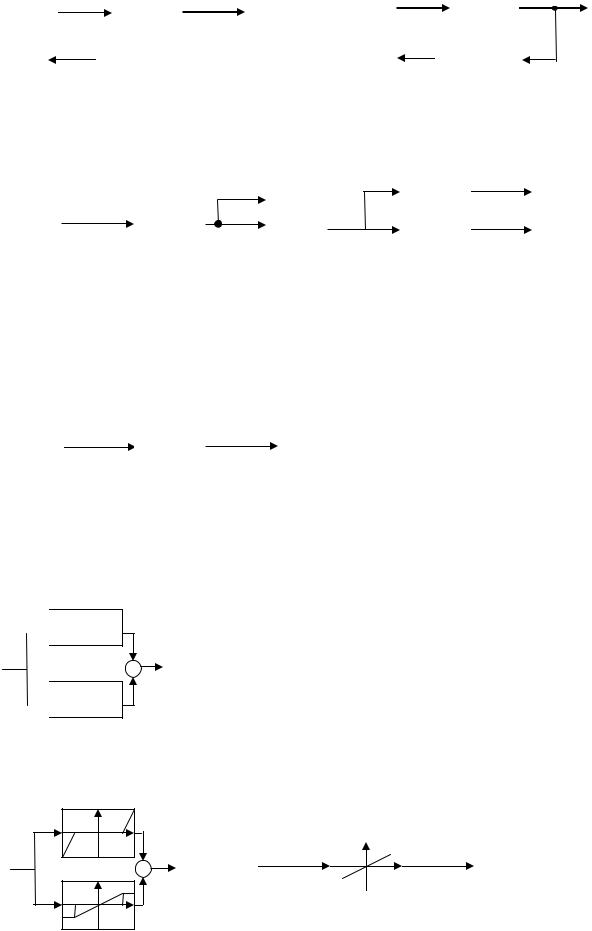
I) Последовательное включение звеньев

Пусть в НЗ «y» зависит от «x» нелинейно.

Для того чтобы сделать связь между y и x линейной можно последовательно с этим НЗ включить другое НЗ с обратной характеристикой.

Рис. 26.19

y = F-1(y1) = F-1[ F(x1)] = x

Это свойство используется для преобразования структурных схем

216

б

а

27. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ НА ОСНОВЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ НЕЛИНЕЙНОСТЕЙ

27.1. Метод гармонической линеаризации нелинейностей

Из-за трудностей описания нелинейные системы обычно сводят, если это возможно к линейным.

Ранее была рассмотрена линеаризация в близи рабочей точки, однако она требует непрерывных функций и малых отключений это – линеаризация во временной области.

Гармонической линеаризация – это линеаризация в частотной области. При этом нелинейный элемент заменяется линейным, но эквивалентным исходному только относительно основной составляющей колебаний. Гармоническая линеаризация может успешно применяться в случае разрывных кривых и значительных отклонений переменных.

Этот метод нашел широкое применение для определения автоколебательных процессов и устойчивости нелинейных систем.

Является мощным методом исследования, так как применяется для систем любого порядка.

Единственное ограничение: необходимо, чтобы линейная часть системы обладала хорошими фильтрующими свойствами, то есть подавляла все гармоники, кроме первой.

Пусть имеем НЗ, которое описывается уравнением:

218

Эта операция называется гармонической линеаризацией.

Если на входе НЗ действует сигнал с постоянной амплитудой и частотой, то q и q` являются постоянными. Таким образом, коэффициенты линеаризации будут постоянны при постоянных значениях a и ω, то есть в случае периодического процесса. Однако в общем случае это условие не выполняется и коэффициенты q и q` будут переменными и зависят от амплитуды входного сигнала и его частоты.

Рассмотрим гармоническую линеаризацию для простой нелинейной зависимости

x2 = F(x1 )

Здесь возможны два случая.

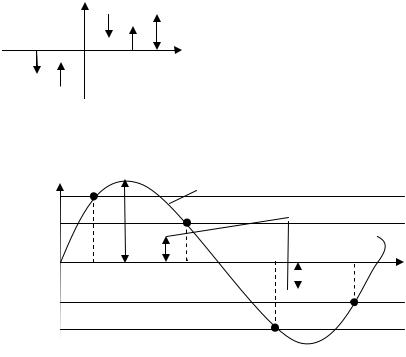
1. Нелинейная характеристика имеет петлю гистерезиса.

В этом случае выходной сигнал будет зависеть от знака производной входного сигнала.

220

ψ2

q(a) = π2a ∫C sin(ψ )dψ ,

ψ1

где С – амплитуда сигнала на выходе НЗ, q(a) = 2πaC (cosψ1 −cosψ2 ) ,

3.b = 0

q'(a) 0.

x2 4С

Сπ

x1

x1=a

a

Гармоническая линеаризация означает замену ломаной линии некоторой прямой

Причем наклон зависит от амплитуды входного сигнала. Чем больше амплитуда входного сигнала, тем более полого располагается прямая, то есть коэффициент q(a) уменьшается с ростом амплитуды входного сигнала. Заменив нелинейное уравнение некоторым линейным, можно анализировать процессы, происходящие в нелинейной системе.

На основе гармонической линеаризации нелинейностей разработано несколько методов. Все они приближенные, так как при этом пренебрегают высшими гармониками в выходном сигнале нелинейного элемента.

27.3. Метод гармонического баланса

Метод разработан Гольдфарбом и относится к числу приближенных методов исследования нелинейных систем. В основе лежит принцип гармонической линеаризации.

Пусть нелинейная система состоит из нелинейного звена, описываемого уравнением

и линейной части с передаточной функцией Wл(p), тогда получим структурную схему

где ωп - частота автоколебаний в системе.

222

Пусть линейная часть системы обладает фильтрующими свойствами, то есть сигнал x2, проходя через линейную часть системы, теряет все высшие гармоники.

Предположение о том, что линейная часть системы подавляет высшие гармоники, называется гипотезой фильтра. АЧХ линейной части часто имеет вид

Рис. 27.12

Поэтому сигналы с частотой ω > 3ω1 существенно ослабляются и ими можно пренебречь.

С учетом этого уравнение (27.12) можно записать

Сравнивая (27.11) и (27.13) для нелинейного звена, можно увидеть аналогию с линейным звеном. Поэтому, как и для линейных звеньев, вводится понятие комплексного коэффициента усиления Н.З.

где ψ =ω t .

Если нелинейная характеристика F(x1) не имеет петли гистерезиса, то

q`(a) = 0 и φн(a) = 0.

27.4. Условие гармонического баланса

Для нелинейной системы на рис. 27.11 можно записать.