Контрольные вопросы:

1. Непрерывная случайная величина.

2. Плотность вероятности непрерывной случайной величины.

3. Свойства плотности распределения вероятностей.

4. Условие нормировки.

5. Вероятность попадания в интервал непрерывной случайной величины.

6. Основные характеристики непрерывной случайной величины.

Контрольные задания:

1. Непрерывная случайная величина задана функцией распределения

.

Требуется:

а) найти постоянную ,

б) найти плотность распределения f(x),

в) построить графики f(x) и F(x),

г) найти Р(1,5<Х<2),

д) найти параметры распределения.

2. Непрерывная случайная величина задана плотностью вероятности

.

а) найти функцию распределения F(x),

б) построить графики f(x) и F(x),

в) найти Р(),

г) найти параметры распределения.

Задания для домашней работы:

Непрерывная случайная величина задана функцией распределения

.

Требуется:

а) найти плотность распределения f(x),

б) построить графики f(x) и F(x),

г) найти Р(0,25<Х<0,5),

д) найти параметры распределения.

Тема №9 «Основные законы распределения случайных величин»

Цель: познакомиться с основными законами распределения дискретных и непрерывных случайных величин, научиться применять их при решении задач теории вероятностей прикладного характера.

Краткие теоретические сведения:

Случайная величина Х имеет биномиальное распределение с параметрами n и p, где и 0<p<1, если , k=0,1,…,n.

, .

Случайная величина имеет распределение Пуассона с параметром , если она принимает целые неотрицательные значения с вероятностями, которые определяются по формуле , k=0,1,…

, .

Случайная величина имеет геометрическое распределение с параметром р (0<p<1), если она может принимать только натуральные значения с вероятностями , .

, .

Случайная величина имеет гипергеометрическое распределение с параметрами m и n, , если она принимает целые неотрицательные значения с вероятностями .

, .

Случайная величина имеет равномерное распределение на отрезке , если её распределение задаётся плотностью .

Функция равномерного распределения .

, .

Случайная величина имеет показательное распределение с параметром , если её распределение задаётся плотностью .

Функция показательного распределения .

, .

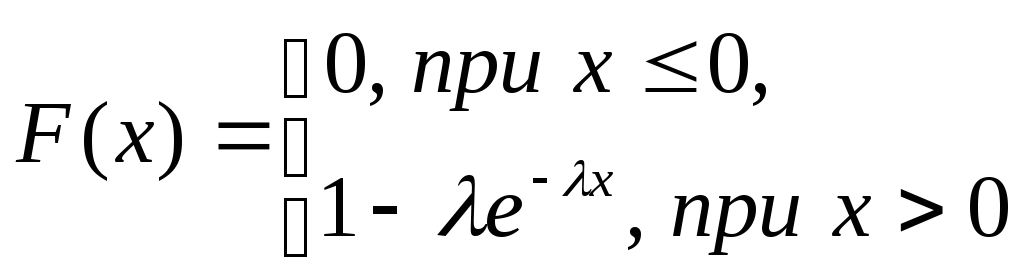Cлучайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами и , если ее плотность вероятности имеет вид:

Кривую нормального закона распределения называют нормальной или Гауссовой кривой.

Математическое ожидание случайной величины , распределенной по нормальному закону, равно параметру этого закона, то есть , а ее дисперсия – параметру , то есть .

Функция распределения нормальной случайной величины , выражается через функцию Лапласа по формуле:

.

Свойства случайной величины, распределенной по нормальному закону:

1) Вероятность попадания случайной величины , распределенной по нормальному закону, в интервал (х₁;х₂), равна

,

где ,

2) Вероятность того, что отклонение случайной величины , распределенной по нормальному закону, от математического ожидания не превысит величину , равна

, где .

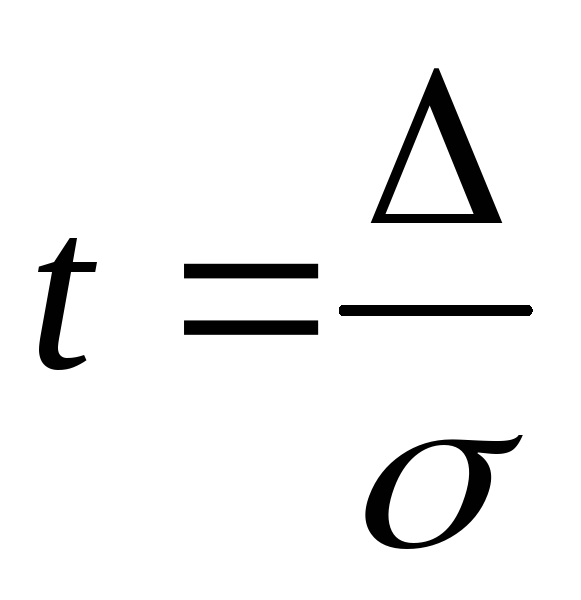Правило «трех сигм»:

Если случайная величина имеет нормальный закон распределения с параметрами и , то есть , то достоверно, что ее значения заключены в интервале .

Нормальный закон распределения случайной величины с параметрами , , то есть называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10;50).

Решение. х₁=10, х₂=50, σ =10, =30.

P(10<Х<50)==2Ф(2).

Из таблицы находим Ф(2)=0,4772 и окончательно имеем

P(10<Х<50)=2·0,4772=0,9544.